Simulation Details¶
Including the required Python libraries¶
Python libraries are included in a file by placing
import PythonLibrary as pl
at the beginning of the file. Here, PythonLibrary is the name of the
Python library to be included, and pl is the
namespace
where the contents of this module are placed. As an example, if we wanted to
include MPSPyLib and call the function Ops.BuildSpinOperators() from
this library, we would use the code
import MPSPyLib as mps
Operators = mps.BuildSpinOperators()
Note the use of the namespace identifier mps to specify that
Ops.BuildSpinOperators() comes from MPSPyLib. In addition to
MPSPyLib, which is always required for MPS simulations, we will also
frequently include NumPy, as it provides the matrix functionality used
internally for the code. We will use the namespace identifier np for NumPy.
Specifying the parameters of a simulation¶
A simulation is specified in MPSPyLib as a Python dictionary of simulation data.
A Python dictionary, also called a
hash table, is
an unordered collection of key:value pairs. For example, we could
construct a dictionary which has a single key 'name' which maps to the
string 'fred' as
mydict = {'name' : 'fred'}
A dictionary is specified by curly braces, 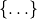 , with
key:value pairs separated by a colon,
, with
key:value pairs separated by a colon, :, which assigns each key to a
value. In python dictionaries, the keys can be any type of immutable data
(i.e. strings, tuples, or numbers). Each key must be unique to the dictionary.
The values assigned to each key is not necessarily unique, and can be any data
type. The value corresponding to a key is accessed by calling that element of
the dictionary using square brackets, ![\left[ \ldots \right]](../_images/math/16e4c8f430a409bcd1d04853b2fb563d41133fe2.png) , referring
to the dictionary name
, referring
to the dictionary name mydict and the key 'name' with the command
mydict['name'].
We will refer to the Python dictionary specifying a simulation in MPSPyLib as
parameters. Every simulation must have the non-optional keys listed in
the table in tools.WriteFiles(). Furthermore optional parameters
are available if the default values are not suitable for the goal of the
simulation.
The particular choice of these parameters defines which algorithms are to be
used and their convergence properties. In addition, parameters should also
contain the values of the Hamiltonian parameters used to define the
Hamiltonian, see Sec. Defining the Hamiltonian and other many-body operators. The simulation specification parameters
is converted into simulation data which is readable by the Fortran backend using
the function
MainFiles = mps.WriteFiles(parameters, Operators, H)
where Operators specifies the operators defining the on-site Hilbert space,
see Sec. Defining local operators, and H specifies the Hamiltonian, see
Sec. Defining the Hamiltonian and other many-body operators. The specification of simulations parameters can also
be a list of dictionaries, which allows for easy batching and parallelization
of simulations. A full set of examples are included in the Examples
subdirectory of OSMPS.
Defining local operators¶
Overview of operators in MPSPyLib¶
The way that ordinary, meaning non-symmetry-adapted, operators are stored
in MPSPyLib are as dictionaries, which are unordered collections of
key:value pairs (Symmetry-adapted operators are discussed in Sec.
Abelian symmetries). This means that the set of operators is stored as a
dictionary, call it Operators, and
Operators['tag']
returns the matrix representation of the operator 'tag' as a
NumPy array.
The default operators built by the convenience functions are listed in a
table inside of the function description. The options are spin operators
from Ops.BuildSpinOperators(), bosonic operators defined in
Ops.BuildBoseOperators(), fermionic operators created by the
function Ops.BuildFermiOperators(), or operators for a Bose-Fermi
system Ops.BuildFermiBoseOperators() building all operators present
in the bosonic and fermionic set. The total number operator 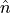 with the key
with the key 'ntotal' is built in addition for the latter one. For more
information on the optional arguments of these functions, one can use the
help functionality of Python as alternative to this documentation, e.g.
help(mps.BuildBoseOperators)
within the Python interpreter.
New operators can be defined by arithmetic on existing operators, and the new operator is designated by a user-defined key. As an example, consider that one wants to construct the bosonic on-site interaction operator
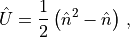
and call it 'Interaction'. This may be achieved as
import MPSPyLib as mps
import numpy as np
Operators = mps.BuildBoseOperators(Nmax=2)
Operators['Interaction'] = 0.5 * (np.dot(Operators['nbtotal'], Operators['nbtotal']) - Operators['nbtotal'])
Here, np.dot is matrix-matrix multiplication from the NumPy libraries.
Operators with internal degrees of freedom¶
MPSPyLib contains two different methods for generating operators for particles
with internal degrees of freedom. The first is to include a value for the spin
of the particle in Ops.BuildBoseOperators() or
Ops.BuildFermiOperators(). In that case each operator from the set
of operators, with the exception of the total number and Fermi
phase operators, obtains a spin projection index e.g. tag_m, where m
runs from 0 to 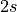 , with
, with  the spin. In addition, the number
operators in each component
the spin. In addition, the number
operators in each component n*_m and the spin operators '*sz,
'*splus, and '*sminus are built, where *=b for bosons and *=f
for fermions.
The second means of producing particles with internal degrees of freedom in
MPSPyLib is through specifying a nonzero value for the nFlavors optional
argument of Ops.BuildBoseOperators() or
Ops.BuildFermiOperators(). In this case each operator from the set
of operators, with the exception of the total number operator,
obtains a flavor projection index e.g. tag_m, where m runs from 0
to nFlavors-1, and the number operators in each component n*\_m are
built, where *=b for bosons and *=f for fermions. If both spin
and nFlavors are nonzero, then the operators are indexed as
'tag\_flavor\_m', where flavor runs from 0 to nFlavors-1 and m
runs from 0 to 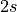 , with
, with  the spin. In
the spin. In
Ops.BuildFermiBoseOperators() different flavors and spins can be
specified for the bosonic and fermionic species. For more information on this
syntax consult the docstring for Ops.BuildFermiBoseOperators().
Finally, we note that the matrix representations of the operators may be
viewed by using the print functionality of python. That is, if we
wanted to see the bosonic destruction operator b, we could call
import MPSPyLib as mps
import numpy as np
Operators = mps.BuildBoseOperators(Nmax=2)
print(Operators['b'])
Likewise, we can print all the operators as
for i in Operators:
print(Operators[i])
Defining the Hamiltonian and other many-body operators¶
Matrix Product Operators¶
The matrix product operators organize the class mpo.MPO. The
natural operator structure for MPS algorithms is a matrix product operator
(MPO). The exact diagonalization modules uses the same class to construct
Hamiltonians, effective Hamiltonians, and operators in Liouville space.
Operators can be constructed as MPOs using a set of rules which specify
how operators acting on local Hilbert spaces are combined to create an operator
acting on the entire many-body system. Using a canonical form for MPOs, several
operators constructed from these rules can be put together as a single
MPO [WC12]. OSMPS uses this essential idea of creating
operators from a set of predetermined rules to construct the Hamiltonian and
other operators appearing in an MPS simulation.
An operator acting on the many-body state, i.e. the MPO, is an object of the
mpo.MPO class in MPSPyLib. For an instantiation of the MPO class,
named H in the following, is obtained as
H = mps.MPO(Operators)
Once we have an MPO object, we add terms to it using the
Ops.AddMPOTerm() method. In particular, the rules are
defined in the module mpoterm.
MPO Terms to build rule sets¶
The following MPO terms are available at present
siterule (mpoterm.SiteTerm). Example:
H.AddMPOTerm('site', 'sz', hparam='h_z', weight=1.0)generates
, where
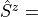
Operators['sz']}andOperatorswas already passed when creating the instance of the MPO. The second argument contains the relevant keys of the operators to be used. Because only the names of the operators are used, this routine handles ordinary and symmetry-adapted operators on the same footing.
bondrule (mpoterm.BondTerm). Example:
H.AddMPOTerm('bond', ['splus','sminus'], hparam='J_xy', weight=0.5)generates
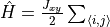
, where
denotes all nearest neighbor pairs
and
,
H.AddMPOTerm('bond', ['sz', 'sz'], hparam='J_z', weight=1.0)generates
, and
H.AddMPOTerm('bond', ['fdagger', 'f'], hparam='t', weight=-1.0, Phase=True)generates
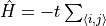
, where
is a fermionic destruction operator. That is, terms with Fermi phases are cared for with the optional
Phaseargument and Hermiticity is automatically enforced by this routine. The Fermi phase is added through a Jordan-Wigner string of the operators inOperatorwith keyFermiPhase. The functionsOps.BuildFermiOperators()andOps.BuildFermiBoseOperators()discussed in Sec. Defining local operators both create the Fermi phase operator appropriate for this use automatically. Notice that the order of the operators matters due to the Jordan-Wigner transformation. Adding['f', 'fdagger']does not result in the same fermionic Hamiltonian. A warning will be printed for obvious cases.
exponentialrule set (mpoterm.ExpTerm). Example
H.AddMPOTerm('exponential', ['sz', 'sz'], hparam='J_z', decayparam=a, weight=1.0)generates
. This rule also enforces Hermiticity and cares for Fermi phases as in the bond rule case.
FiniteFunctionrule (mpoterm.FiniteFunc). Example:
f = [] for ii in range(6): f.append(1.0 / (ii + 1.0)**3) H.AddMPOTerm('FiniteFunction', ['sz', 'sz'], f=f, hparam='J_z', weight=-1.0)generates
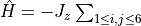
, where the summation is over all
and
pairs separated by at least
and at most
lattice spacings. The range of the potential is given by the number of elements in the list
f. This rule enforces Hermiticity and cares for Fermi phases as in the bond rule case.
InfiniteFunctionrule set (mpoterm.InfiniteFunc). We point out that this term is always fitted with a set ofmpoterm.ExpTermfor MPS simulations. Examples:
invrcube = lambda x: 1.0/(x*x*x) H.AddMPOTerm('InfiniteFunction', ['sz', 'sz'], hparam='J_z', weight=1.0, func=invrcube, L=1000, tol=1e-9)generates
, where the functional form is valid to a distance
Lwith a residual of at mosttol. Similarly,H.AddMPOTerm('InfiniteFunction', ['sz', 'sz'], hparam='J_z', weight=1.0, x=x, y=f, tol=1e-9)generates
, where the functional form
is determined by the array of values
fand the array of evaluation pointsx. The distance of validityLis determined from the arrayx. This rule applies only to monotonically decreasing functionsfuncorf, and so outside the range of validityLthe corrections are also monotonically decreasing. This rule enforces Hermiticity and cares for Fermi phases as in the bond rule case.
productrule (mpoterm.ProductTerm). Example:
H.AddMPOTerm('product', 'sz', hparam='h_p', weight=-1.0)generates
. The operator used in the product must be Hermitian.
MBStringrule set(mpoterm.MBStringTerm). See function description for usage.mpoterm.TTerm. See function description for usage.mpoterm.SiteLindXX. See function description for usage.mpoterm.LindExp. See function description for usage.mpoterm.LindInfFunc. See function description for usage.mpoterm.MBSLind. See function description for usage. (Can act as nearest neighbor Lindblad term.)
In all of the above expressions, H is an object of the MPO class.
The strings passed to the argument hparams represent tags for variable
Hamiltonian parameters, which allow for easy batching and parallelization
(Sec. Running a parallel static simulation), and also facilitate dynamical processes
The argument hparams is optional, and defaults to the constant
value 1. The optional argument weight specifies a constant factor that
scales the operator and defaults to the value 1, too.
Developer’s Guide for Rule Sets
Module contains a class for each possible term in the MPO rule sets. Each term is derived from a base class.If you plan to add additional MPO terms to OSMPS, you have to modify the following files. In the case of a new Lindblad operator, these are
mpoterm.py: add class for the new term
mpo.py: add new term to the MPO structure and enable writing.
MPOOps_types_templates.f90: define derived type and add to MPORuleSet
MPOOps_include.f90: add read/destroy methods for RuleSets
MPOOps_include.f90: effective Hamiltonian for 2 sites
MPOOps_include.f90: Liouville operator for 2 sites
MPOOps_include.f90: effective Hamiltonian represented as MPO.
MPOOps_include.f90: Liouville operator represented as MPO.
TimeevolutionOps_include.f90: Add overlaps to QT functionality.
Example
As an example, a template MPO for the Hamiltonian of the hard-core boson model
with  interactions,
interactions,
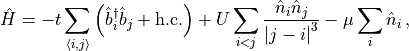
is provided by
import MPSPyLib as mps
# Build operators
Operators = mps.BuildBoseOperators(1)
# Define Hamiltonian MPO
H = mps.MPO(Operators)
H.AddMPOTerm('site', 'nbtotal', hparam='mu', weight=-1.0)
H.AddMPOTerm('bond', ['bdagger', 'b'], hparam='t', weight=-1.0)
invrcube = lambda x: 1.0/(x*x*x)
H.AddMPOTerm('InfiniteFunction', ['nbtotal', 'nbtotal'], hparam='U',
weight=1.0, func=invrcube, L=1000, tol=1e-9)
We stress that no assumptions are made about the hparam parameters 't',
'mu', or 'U' when the MPO is built. The hparams are simply tags
parameterizing the operators which appear in the Hamiltonian. The actual
numerical values of 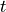 ,
, 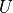 , and
, and 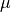 are specified as
part of the dictionary
are specified as
part of the dictionary parameters discussed in Sec. Specifying the parameters of a simulation.
These parameters can also be position-dependent, as demonstrated in the example
files in OpenMPS Examples.
One can print operators using the mpo.MPO.printMPO() method. As an
example, the interacting spinless fermion model
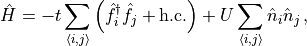
is specified and printed as
import MPSPyLib as mps
# Build operators
Operators = mps.BuildFermiOperators()
# Define Hamiltonian MPO
H = mps.MPO(Operators)
H.AddMPOTerm('bond', ['fdagger', 'f'], hparam='t', weight=-1.0, Phase=True)
H.AddMPOTerm('bond', ['nftotal', 'nftotal'], hparam='U', weight=1.0)
H.printMPO()
The result of this code is
-1.0 * t * sum_i fdaggerP_i f_{i+1} + 1.0 * t * sum_i fP_i fdaggerP_{i+1} + 1.0 * U * sum_i nftotal_i nftotal_{i+1}
Note the use of the phased operators fdaggerP and fP according to
Phase=True.
As the 'InfiniteFunction' rule constructs MPOs by fitting the decaying
function to a series of weighted exponentials, the result of printMPO
will contain the data for the exponentials and not information about the
infinite function proper.
Finally, as complex MPOs with InfiniteFunction interactions can be
expensive to generate, one can save the data in an MPO object instance
using the mpo.WriteMPO() function, and then read it in later using
the mpo.ReadMPO() function. The syntax for these is
mps.WriteMPO(H,filename)
H = mps.ReadMPO(filename)
where H is an object of the mpo.MPO class and filename is
the name of the file where the MPO is written to/read from.
Defining and reading observables: obsterms.Observables¶
Defining Observables¶
Module obsterms defines the observables on quantum systems. Each observable
contains the corresponding methods to write the fortran files and to read the
results from the fortran outputs. The following observables are defined
Observables on any quantum sytem in OSMPS are specified by instantiating an
object of the obsterms.Observables class, for example
myObservables = Observables(Operators)
One then adds observables using the obsterms.Observables.AddObservable()
method. Each observable is itself a python class and has the corresponding
read/write methods Examples of the use of
obsterms.Observables.AddObservable() are:
siteobservables (obsterms.SiteObservable). Example :
myObservables.AddObservable('site', 'nbtotal', name='n')will measure
at each site and return the result as a length-
vector with the tag
'n'. Recall thatis either the system size in the case of a finite MPS or the unit cell length in the case of iMPS as specified in the table in the description of
WriteFiles()
Site entropy measurement (
obsterms.SiteEntropyObservable).Bond entropy measurement (
obsterms.BondEntropyObservable).corrobservables (obsterms.CorrObservableandobsterms.FCorrObservable). Example:
myObservables.AddObservable('corr', ['nbtotal', 'nbtotal'], name='nn')will measure
at each independent pair of sites
and return the result with the tag
'nn'. For finite-size MPS simulations the result is returned as anmatrix, and for infinite-size MPS simulations the result is returned as a length-
vector, where
is specified by the
SpecifyCorrelationRangemethod, see Sec. Infinite-size ground state search: iMPS. For observables involving odd numbers of fermionic operators on a given site, there is an optionalPhaseargument such as existed for thempo.MPO.AddMPOTerm()method. An example ismyObservables.AddObservable('corr', ['fdagger', 'f'], name='spdm', Phase=True)which measures the fermionic correlation function
.
stringobservables (obsterms.StringCorrObservable). Example (fromInfiniteheisenbergspinone.py):
myObservables.AddObservable('string', ['sz', 'sz', 'phaseString'], name='StringOP')will measure
at each independent pair of sites
and return the result with the tag
'StringOP'. Note thatphaseStringhas been defined to beonly in this particular case.
MPOobservables (obsterms.MPOObservable). Example:
DefectDensity = mps.MPO(Operators) DefectDensity.AddMPOTerm('bond', ['sz', 'sz']) myStaticObservables.AddObservable('MPO', DefectDensity, 'Defect Density')will measure
and return the result with the tag
'Defect Density'. In this way, essentially arbitrary many-body operators may be measured.
Reduced density matrix, limited to one (
obsterms.RhoiObservable) or two (obsterms.RhoijObservable) sites at present, can be measured as well. They can be added once as single item or list. An empty list indicates to report the singular values at all bipartitions. If passed as list, entries have to sorted ascending.
myObservables.AddObservables('DensityMatrix_i', []) myObservables.AddObservables('DensityMatrix_ij', [])
It is possible to measure the mutual information matrix without writing all the information about the reduced density matrices to the result files (
obsterms.MutualInformationObservable).myObservables.AddObservables('MI', True)
The Schmidt values (
obsterms.LambdaObservable) at the bipartitions are another measurement, which gives a more detailed picture than the bond entropy. They can be added once as single item or list. An empty list indicates to report the singular values at all bipartitions.
myObservables.AddObservables('Lambda', [])
Distance to a pure state (
obsterms.DistancePsiObs)Save state independent from checkpoints etc. (MPS only,
obsterms.StateObservable)Gate observables (ED only,
obsterms.GateObservable).Distance to a density matrix (ED only,
obsterms.DistanceRhoObs).
Observables for the different algorithms in OSMPS are specified as part of the
parameters dictionary, see Table in tools.WriteFiles().
Developer’s Guide for new observables
Implement new class in this module, i.e.
obsterms. We need the minimal class functions__init__,add,write, andread.Add new observable to the
dataset andmpslistin :py:class:Observables.Modify
ObsOps_types_templates.f90by adding a new observable toOBS_TYPEand possibly defining a new derived type for this observable.Define read, write, and destroy methods as far as applicable.
Carry out measurements in all
observesubroutines.
Reading Observables¶
The observables which correspond to static algorithms such as MPS and eMPS,
see Sec. Algorithms of the OpenMPS, are read using the
obsterms.ReadStaticObservables() function taking the parameters
dictionary as argument. Here, the observables for MPS are specified by the key
'MPSObservables' in 'parameters' and, similarly, the key
'eMPSObservables' in 'parameters' specifies the observables for eMPS,
see Table in tools.WriteFiles(). The output from
obsterms.ReadStaticObservables() is a list of dictionaries. The number of
elements in the list is equal to the number of individual simulations. An
element of this list contains all of the relevant simulation metadata from
parameters as well as the observables specified in myObservables with
the tags given by the obsterms.Observables.AddObservable() method. That is,
Output['n'] outputs the observable 'n' as tagged by
obsterms.Observables.AddObservable() for the dictionary Output which is an
element of Outputs. The tags of the various default information returned
from obsterms.ReadStaticObservables() can be found in the function
documentation.
In addition to the observables which are specified using the
obsterms.Observables.AddObservable() method, the von Neumann entropy of
entanglement of a given site 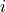 with the rest of the system,
with the rest of the system,
![S_{\mathrm{site},i}&\equiv -\mathrm{Tr}\left[\hat{\rho}_i\log\hat{\rho}_i\right]\, ,\;\;\; \hat{\rho}_i\equiv \mathrm{Tr}_{j\ne i}|\psi\rangle\langle \psi|](../_images/math/f0c98e253b06a27a95f5eec22642acbd42dd897a.png)
is measured whenever not deactivated. The result
is stored as an 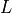 -length vector with the tag
-length vector with the tag 'SiteEntropy'.
Additionally, the von Neumann entropy of entanglement of bipartition 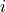
![S_{\mathrm{bond},i}&\equiv -\mathrm{Tr}\left[\hat{\rho}_i\log\hat{\rho}_i\right]\, ,\;\;\; \hat{\rho}_i\equiv \mathrm{Tr}_{j\ge i}|\psi\rangle\langle \psi|](../_images/math/5d8da9453851f96257b8c8d358fe39b5c4407223.png)
is measured whenever not deactivated. For
finite-size MPS simulations, the result is stored as an
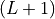 -length vector with the tag
-length vector with the tag 'BondEntropy'. For
infinite-size MPS simulations, 'BondEntropy' is always measured, and is a
scalar indicating the entropy of entanglement of the bipartition between any
two adjacent unit cells.
For finite-size systems, the total energy 'energy' and the variance
'variance' 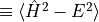 are always measured.
The quantity
are always measured.
The quantity 'converged' returns a value of 'T' or 'F' depending
on whether the variance met the desired user-defined tolerance or not,
respectively. For infinite-sized systems, the energy is replaced by
'energy_density', and the 'convergence' is determined from the
orthogonality fidelity as discussed in Sec. Infinite-size ground state search: iMPS. Finally, in all
cases, the maximum bond dimension of the MPS is returned as
'bond_dimension'.
To extract observables from tMPS simulations, the function
obsterms.ReadDynamicObservables() taking the paramaeters dictionary
as argument is used. The observables for tMPS are specified by the key
'DynamicsObservables' in 'parameters'. The default observables returned
from obsterms.ReadDynamicObservables() are given in its function description.
The number of elements of Outputs corresponds to the number of elements of
parameters, but each element of Outputs is itself a list whose length
is the number of time steps. These elements are distinguished by the key
'time'. Time is measured in units of 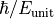 , where
, where
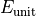 is the unit of energy set by the magnitudes of the
Hamiltonian parameters.
is the unit of energy set by the magnitudes of the
Hamiltonian parameters.
Specification of dynamics¶
A dynamical process simulated with tMPS, details on the algorithms can be
found starting at Sec. Krylov-based time evolution : tMPS, is
specified as an object of the Dynamics.QuenchList class. An object
of this class is obtained as
Quenches = mps.QuenchList(H)
where H is an MPO.MPO object specifying the MPO of the
Hamiltonian used to time-evolve the state. Dynamical processes, which we will
call quenches, are added using the Dynamics.QuenchList.AddQuench()
method with the syntax
Quenches.AddQuench(Hparams, time, deltat, funcs, ConvergenceParameters=None, stepsforoutput=1)
Here Hparams is a list of the tags of the Hamiltonian
parameters in H which are to be modified during the quench, time is the
total time of this quench, deltat is the desired numerical time step,
funcs is a list of functions specifying how the Hamiltonian parameters given
in Hparams change in time. ConvergenceParameters is used to specify the
time evolution algorithm used and its convergence parameters for this quench.
The available options are the
convergence.KrylovConvParam, convergence.TEBDConvParam,
convergence.TDVPConvParam. and convergence.LRKConvParam.
Finally, stepsforoutput denotes the number time steps between
measurements of the state. The functions in funcs should take a single
argument which is the time. At present, dynamics always begins from the ground
state, and the Hamiltonian used for time evolution must have the same form as
the Hamiltonian used for dynamics. That is, the two Hamiltonians must have the
same Hamiltonian parameters and these parameters must be of the same numerical
type, e.g. if a parameter is site-dependent for statics it must also be
site-dependent for dynamics and vice versa.
It is useful here to consider a specific example. We consider quenching the
parameter 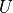 in the Bose-Hubbard model
in the Bose-Hubbard model
![\hat{H}&=-t\sum_{\langle i,j\rangle}\left[\hat{b}_i^{\dagger}\hat{b}_j+\mathrm{h.c.}\right]+U\sum_{i}\frac{\hat{n}_i\left(\hat{n}_i-1\right)}{2}](../_images/math/03a501b89962ae1ea50c0bb4b4c1c98e8ff96ef8.png)
linearly from 10 to 1, and then linearly back to 10 over a time 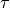 .
Using the Hamiltonian specification
.
Using the Hamiltonian specification
Operators = mps.BuildBoseOperators(5)
Operators['interaction'] = 0.5 * (np.dot(Operators['nbtotal'], Operators['nbtotal']) - Operators['nbtotal'])
H = mps.MPO(Operators)
H.AddMPOTerm('bond', ['bdagger', 'b'], hparam='t', weight=-1.0)
H.AddMPOTerm('site', 'interaction', hparam='U', weight=1.0)
this quench process is generated as
# Quench function ramping down
def Ufuncdown(t, tau=tau):
return 10.0 + 2.0 * (1.0 - 10.0) * t / tau
# Quench function ramping back up
def Ufuncup(t, tau=tau):
return 1.0 + 2.0 * (10.0 - 1.0) * (t - 0.5 * tau) / tau
Quenches = mps.QuenchList(H)
Quenches.AddQuench(['U'], 0.5 * tau, min(0.5 * tau / 100.0, 0.1), [Ufuncdown], ConvergenceParameters=myKrylovConv)
Quenches.AddQuench(['U'], 0.5 * tau, min(0.5 * tau / 100.0, 0.1), [Ufuncup], ConvergenceParameters=myKrylovConv)
for a given tau and convergence parameters myKrylovConv. We note two
important items regarding the functions Ufuncdown and Ufuncup which
specify how 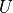 changes in time. The first is that time is measured from
the end of the last quench and not from the beginning of the current quench.
This accounts for the
changes in time. The first is that time is measured from
the end of the last quench and not from the beginning of the current quench.
This accounts for the (t-0.5*tau) in the latter quench function. The second
is that tau is included as an optional argument in the functions, and
assigned the desired value. If we had instead used the functions
# Quench function ramping down
def Ufuncdown(t):
return 10.0 + 2.0 * (1.0 - 10.0) * t / tau
# Quench function ramping back up
def Ufuncup(t):
return 1.0 + 2.0 * (10.0 - 1.0) * (t - 0.5 * tau) / tau
this can lead to incorrect results when looping over tau due to a technical point of python. Generally, any values which are to be looped over in the function definitions should be specified as optional arguments in this fashion.
Abelian symmetries¶
A particularly important numerical optimization for MPS algorithms is to
respect global symmetries. Respecting a symmetry corresponds to fixing
the quantum number 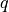 associated with an operator
associated with an operator 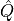 which commutes with the Hamiltonian
which commutes with the Hamiltonian 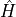 . We will call these
quantum numbers charges. OSMPS has the ability to simultaneously
conserve an arbitrary number of global U(1) symmetries, which is the most
common type of symmetry found in lattice models. For the Abelian group U(1),
the total charge of a many-body state corresponds to the sum of the charges
of its constituents. That is to say, the total charge operator
. We will call these
quantum numbers charges. OSMPS has the ability to simultaneously
conserve an arbitrary number of global U(1) symmetries, which is the most
common type of symmetry found in lattice models. For the Abelian group U(1),
the total charge of a many-body state corresponds to the sum of the charges
of its constituents. That is to say, the total charge operator 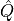 may be written
may be written
(1)¶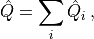
where 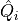 is the charge operator for site
is the charge operator for site 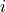 , which we
will call the generator of the symmetry. To conserve charges in OSMPS, one
specifies the generators
, which we
will call the generator of the symmetry. To conserve charges in OSMPS, one
specifies the generators 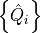 and their
associated charges. The generators are specified as a list of the keys of the
generators in the dictionary of Operators
and their
associated charges. The generators are specified as a list of the keys of the
generators in the dictionary of Operators Operators, see
Sec. Defining local operators. This list of keys is then the value
corresponding to the key 'Abelian_generators' in the dictionary
parameters of simulation data, see Sec. Specifying the parameters of a simulation.
The charges are specified as a list of numerical data with the same length as
the list of generators, and is the value corresponding to the key
'Abelian_quantum_numbers' in parameters. We note that the generators
must be diagonal matrices, and an exception will be thrown if this is not the
case. For non-standard symmetries, the operators may be made diagonal by
performing matrix operations on the values of the dictionary Operators as
discussed in Sec. Defining local operators.
In addition to the generators of the symmetry being diagonal, all of the
operators used must be covariant under the group operation. An exception is
thrown if this is not the case. Simply stated, a covariant operator changes
the quantum numbers of a state in a well-defined way. A more complete
definition of covariant operators is given in
Sec. Symmetry-adapted operators of the Developer’s manual. For
example, let us consider a system of bosons with the total particle number
conserved. The destruction operator 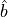 is covariant, as it changes
the particle number by
is covariant, as it changes
the particle number by 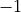 , but the operator
, but the operator
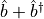 is not covariant, as it does not transform
particle number eigenstates into particle number eigenstates. All operators
which are built by the convenience functions discussed in Sec.
Defining local operators are covariant under the typical group operations, e.g.
all particle operators are covariant under particle number conservation and
all spin operators are covariant under conservation of magnetization.
Operators which are not covariant and are not needed can be removed with the
is not covariant, as it does not transform
particle number eigenstates into particle number eigenstates. All operators
which are built by the convenience functions discussed in Sec.
Defining local operators are covariant under the typical group operations, e.g.
all particle operators are covariant under particle number conservation and
all spin operators are covariant under conservation of magnetization.
Operators which are not covariant and are not needed can be removed with the
RemoveOperator function to avoid the aforementioned exception.
In addition to the U(1) symmetry, we support as well 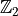 symmetries. One example for such a symmetry is the quantum Ising model with
the odd and even sector.
symmetries. One example for such a symmetry is the quantum Ising model with
the odd and even sector.
At present, conservation of symmetries is only supported for MPS simulations on finite lattices.
Convergence criteria¶
Convergence criteria are specified as objects inheriting from the class
convergence.ConvergenceParameters. Each algorithm has its own
class with the parameters relevant for the algorithm being used. These are
convergence.MPSConvParamfor finite size MPS statics including ground states and excited states.convergence.iMPSConvParamfor infinite size MPS statics.The four time evolution methods for MPS can be adapted with
convergence.KrylovConvParam,convergence.TEBDConvParam,convergence.TDVPConvParam, andconvergence.LRKConvParam.
All classes come with default convergence values and those can be used by simply creating an object of the relevant class, e.g.
myConv = mps.MPSConvParam()
Custom values for the convergence parameters are specified as optional arguments to the object initialization. For example, to set the value of the bond dimension to be 15, one calls
myConv = mps.MPSConvParam(max_bond_dimension=15)
The convergence parameters contained in MPSConvParam and
KrylovConvParam are discussed in Sec. Variational ground state search and
ond example for the dynamics in Sec. Krylov-based time evolution : tMPS, respectively.
For MPS and eMPS simulations which use the convergence.MPSConvParam
class, one can iteratively refine results from previous iterations by
specifying multiple convergence parameters. There are two class methods to do
so. The first is convergence.MPSConvParam.AddConvergenceParameters(),
which has the same arguments as the class instantiation. This includes another
simulation with the new convergence parameters which uses the state obtained
with the previous set of convergence parameters as a variational ansatz. The
second method is
convergence.ConvParam.AddModifiedConvergenceParameters() with the
argumentes refered to as
copywhich, modifywhich, and whichparameters. Here, copywhich
is an integer denoting which of the previous convergence parameters are to be
copied, starting from zero. The arguments modifywhich and
whichparameters are lists specifying which parameters are to be modified
and to what values, respectively. For example, to specify that the state is to
be computed with maximum bond dimensions 15, 20, and 25 consecutively, one
would construct the convergence parameters as
myConv = mps.MPSConvParam(max_bond_dimension=15)
myConv.AddModifiedConvergenceParameters(0, ['max_bond_dimension'], [20])
myConv.AddModifiedConvergenceParameters(0, ['max_bond_dimension'], [25])
For each set of convergence parameters the state is measured, and these outputs
are distinguished by the key 'convergence_parameter', see the key specified
in Table of obsterms.ReadStaticObservables().
The key 'convergence_parameter' is an integer beginning
from 0, with increasing integers denoting convergence parameters added later.
For further examples of this functionality, see the example files in
in Sec. OpenMPS Examples.
Running simulations¶
Running a serial static simulation¶
As discussed in Sec. Specifying the parameters of a simulation, a list of dictionaries
parameters specifying MPS simulations is converted to Fortran-readable
data using the tools.WriteFiles() method as
MainFiles = mps.WriteFiles(parameters, Operators, H)
The output MainFiles is a list of the files to be passed to the Fortran
backend. The simulation is run via
mps.runMPS(MainFiles)
which runs the simulations serially in the order they are specified in the
list parameters.
Running a parallel static simulation¶
OSMPS supports automatic data-parallelism of simulations using MPI (Message Passing Interface). Parallel simulations can be specified in two ways. A list of simulations to be executed as in the serial case or a template where one or multiple parameters can be plugged in from a list. In the following, we explain both variants:
Parallel simulations via a list¶
If you already have a list of simulation, you may just switch from the
function tools.WriteFiles() to tools.WriteMPSParallelFiles().
You need one additional argument, comp_info, which is a dictionary
containing the setting for a computer cluster with the only required argument
the number of nodes. For a better tuning more parameters are available. The
example is then
comp_info = {'nodes' : '4'}
MainFiles = mps.WriteFiles(parameters, Operators, H, comp_info)
This will return the name of script to be submitted to the computer cluster.
This is step replaces the previous call to tools.runMPS(). In case
you want to run the job with MPI on a local machine, you will inside the
script a line containing Execute_MPSParallelMain. This line can
be copied to you command line and starts the MPI simulations.
Parallel simulations via a template¶
We assume that there exist some set of parameters which one wishes to parallelize over. For example, one may wish to parallelize the XXZ model in a magnetic field
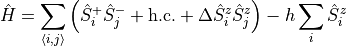
over the anisotropy 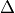 and the magnetic field
and the magnetic field 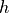 . One begins
by building a template dictionary
. One begins
by building a template dictionary parameters_template for the simulations
which includes all information except for the specification for 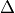 and
and 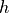 as discussed in Sec. Specifying the parameters of a simulation. The specification of
the parameters
as discussed in Sec. Specifying the parameters of a simulation. The specification of
the parameters 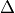 and
and 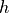 comes through two lists. The first,
called
comes through two lists. The first,
called iterparams, is a list of the tags of the Hamiltonian parameters to
be parallelized over. The second, called iters, is a list whose elements
are a list of the numerical values for the corresponding parameters in
iterparams. For our example of the XXZ model, these two vectors might be
specified as
Deltamin = 0.1
Deltamax = 2.0
Deltavals = 50
Deltaiter = np.linspace(Deltamin, Deltamax, Deltavals)
hmin = 0.0
hmax = 1.0
hvals = 20
hiter = np.linspace(hmin, hmax, hvals)
iterparams = ['Delta', 'h']
iters = [Deltaiter, hiter]
This would parallelize over the 50 values of 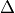 linearly spaced
from 0.1 to 2 and the 20 values of
linearly spaced
from 0.1 to 2 and the 20 values of 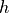 linearly spaced from 0 to 1 for
a total of 1000 points. Note that the tags we use here in
linearly spaced from 0 to 1 for
a total of 1000 points. Note that the tags we use here in iterparams should
match those we use in building the Hamiltonian MPO, see Sec. Defining the Hamiltonian and other many-body operators.
These lists, along with the template dictionary of other metadata, are passed
to the function Paralleltools.WriteMPSParallelTemplate(), with syntax
parameters = mps.WriteMPSParallelTemplate(parameters_template, Operators, H, comp_info, iterparams, iters)
Here, comp_info is a dictionary specifying metadata related to the parallel
environment. The function Paralleltools.WriteMPSParallelTemplate()
writes the files required by the Fortran backend for each individual simulation
as well as two files *jobpool.dat and *progress, where * is the
'job\_ID' specified in the parameters_template dictionary. The jobpool
file contains the main files which specify the individual simulations to be run
together with unique integer tags, and the progress file indicates which of
these tasks has already been completed. Finally,
Paralleltools.WriteMPSParallelTemplate() writes a pbs or slurm script
which will submit a parallel job to your computer’s queueing system. If a job
does not finish all of the tasks in the jobpool, calling
Paralleltools.WriteMPSParallelTemplate() will create a new job pool
containing only simulations which have not been run previously.
An alternate functionality of the parallel code is to pass in a list of
parameters to parameters_template.
Paralleltools.WriteMPSParallelTemplate() will automatically parallelize
over all of the simulations in parameters_template. A list of Hamiltonians
may also be passed to H, but the length of H and
parameters_template must be the same. Finally, the two functionalities
may be combined by specifying both a list of parameters_template as well
as parameters to iterate over via iterparams and iters.
Putting it all together¶
In this section we will analyze the simplest example file given in the
Examples subdirectory of OSMPS, 04_SpinlessFermions.py. The file begins
by importing MPSPyLib, NumPy, and the module sys
1import MPSPyLib as mps
2import numpy as np
3import sys
Inside the function main we start building the spinless operators
1
2 # Build operators
Now, Operators contains the fermion operators given in the table of
Ops.BuildFermiOperators(). We now build the Hamiltonian which consists
only of tunneling,
(2)¶![\hat{H}&=-t\sum_{\langle i,j\rangle}\left[\hat{f}_i^{\dagger}\hat{f}_j+\mathrm{h.c.}\right]\, .](../_images/math/fa27667007b50d07877fa685d8a9bd9de5d264ea.png)
This is done as
1
2 # Define Hamiltonian MPO
3 H = mps.MPO(Operators)
The specification 'bond' denotes the sum over nearest-neighbors in
Eq. (2) and Phase=True denotes that a Fermi phase should be
included, as this term involves an odd number of fermion operators at each
site, see Sec. Defining the Hamiltonian and other many-body operators. We next define the observables we wish to measure
1
2 # Observables
3 myObservables = mps.Observables(Operators)
4 # Correlation functions
5 myObservables.AddObservable('corr', ['fdagger','f'], 'bspdm')
Here, the observable we have called 'spdm' is the fermionic
single-particle density matrix, 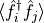 , and the observable we have called
, and the observable we have called 'bspdm' is a single-particle
density matrix 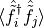 in which the operators
in which the operators 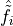 anticommute on a
given site but commute when not on the same site. The difference is in
including
anticommute on a
given site but commute when not on the same site. The difference is in
including Phase=True in the observable specification. We will see the
differences in the two correlation functions when we run the simulation. Next,
we specify the convergence criteria for our simulation as
1
2 # Convergence data
Now, we specify the simulation parameters as
1
2 t = 1.0
3 L = 10
4 N = 5
5
6 # Define statics
7 parameters = [{
8 # Directories
9 'simtype' : 'Finite',
10 'job_ID' : 'SpinlessFermions_',
11 'unique_ID' : 'L_' + str(L) + 'N' + str(N),
12 'Write_Directory' : 'TMP_04/',
13 'Output_Directory' : 'OUTPUTS_04/',
14 # System size and Hamiltonian parameters
15 'L' : L,
16 't' : t,
17 'verbose' : 2,
18 'logfile' : True,
19 # Specification of symmetries and good quantum numbers
20 'Abelian_generators' : ['nftotal'],
21 'Abelian_quantum_numbers' : [N],
L is the number of lattice sites and t is the tunneling energy. Note
that it is only in the dictionary parameters that we specify a value for
t; we do not need to give an actual value for t when we are building
the Hamiltonian. The lines
1 'verbose' : 2,
2 'logfile' : True,
specify that the total number of fermions is conserved, and is set to be N.
We write Fortran-readable files and run them with the lines if we are not in
the post processing mode:
1 'MPSConvergenceParameters' : myConv
2 }]
3
4 # Write Fortran-readable main files
5 MainFiles = mps.WriteFiles(parameters, Operators, H,
6 PostProcess=PostProcess)
7
The observables are read in using
1 if(not PostProcess):
2 if os.path.isfile('./Execute_MPSMain'):
3 RunDir = './'
4 else:
Because we have only a single simulation in this case, corresponding to the
ground state with a single set of convergence parameters, the relevant outputs
are contained in Outputs[0], the first element of the list Outputs, see
Sec. Defining and reading observables: obsterms.Observables. The 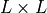 matrix representing the
single-particle density matrix is
matrix representing the
single-particle density matrix is Outputs[0]['spdm'], as we specified the
tag 'spdm' for this observable in line 14. We now diagonalize the
single-particle density matrix and its phaseless counterpart 'bspdm' to
find their eigenvalues using the numpy function eigh and print the
eigenvalues to the screen with
1 mps.runMPS(MainFiles, RunDir=RunDir)
2 return
3
4 # Postprocessing
5 # --------------
6
7 Outputs = mps.ReadStaticObservables(parameters)
8
9 spdm = Outputs[0]['spdm']
The return state indicates the end of the main function. The last lines call
our main function in the case the file is call from command line and handle
the post processing argument from the command line. If it was included as
module the main function would not be executed.
1 bspdmeigs, U = np.linalg.eigh(bspdm)
2
3 print('Eigenvalues of <f^{\dagger}_i f_j> with Fermi phases', spdmeigs)
4 print('Eigenvalues of <f^{\dagger}_i f_j> without Fermi phases', bspdmeigs)
5
6 return
7
8
9if(__name__ == '__main__'):
Calling
osmps@manual:~$ python 04_SpinlessFermions.py
in the terminal gives the output
./Execute_MPSMain TMP/SpinlessFermions_L_10N5Main.nml
Eigenvalues of <f^{\dagger}_i f_j> with Fermi phases [ -4.56780243e-16 -4.34812894e-17 2.50202620e-16
5.99741719e-13 6.00558567e-13 1.00000000e+00 1.00000000e+00 1.00000000e+00
1.00000000e+00 1.00000000e+00]
Eigenvalues of <f^{\dagger}_i f_j> without Fermi phases [ 0.05067985 0.06159355 0.09456777 0.12959356
0.17094556 0.35616646 0.45241313 0.60737271 0.91929511 2.1573723 ]
We see that the properly phased single-particle density matrix produces a sharp Fermi distribution, as expected. Contrariwise, the single-particle density matrix without the Fermi phases displays a macroscopically large eigenvalue.
Footnotes