Python Module mpoterm¶
MPO Terms to build rule sets¶
The following MPO terms are available at present
siterule (mpoterm.SiteTerm). Example:
H.AddMPOTerm('site', 'sz', hparam='h_z', weight=1.0)generates
, where
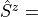
Operators['sz']}andOperatorswas already passed when creating the instance of the MPO. The second argument contains the relevant keys of the operators to be used. Because only the names of the operators are used, this routine handles ordinary and symmetry-adapted operators on the same footing.
bondrule (mpoterm.BondTerm). Example:
H.AddMPOTerm('bond', ['splus','sminus'], hparam='J_xy', weight=0.5)generates
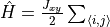
, where
denotes all nearest neighbor pairs
and
,
H.AddMPOTerm('bond', ['sz', 'sz'], hparam='J_z', weight=1.0)generates
, and
H.AddMPOTerm('bond', ['fdagger', 'f'], hparam='t', weight=-1.0, Phase=True)generates
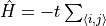
, where
is a fermionic destruction operator. That is, terms with Fermi phases are cared for with the optional
Phaseargument and Hermiticity is automatically enforced by this routine. The Fermi phase is added through a Jordan-Wigner string of the operators inOperatorwith keyFermiPhase. The functionsOps.BuildFermiOperators()andOps.BuildFermiBoseOperators()discussed in Sec. Defining local operators both create the Fermi phase operator appropriate for this use automatically. Notice that the order of the operators matters due to the Jordan-Wigner transformation. Adding['f', 'fdagger']does not result in the same fermionic Hamiltonian. A warning will be printed for obvious cases.
exponentialrule set (mpoterm.ExpTerm). Example
H.AddMPOTerm('exponential', ['sz', 'sz'], hparam='J_z', decayparam=a, weight=1.0)generates
. This rule also enforces Hermiticity and cares for Fermi phases as in the bond rule case.
FiniteFunctionrule (mpoterm.FiniteFunc). Example:
f = [] for ii in range(6): f.append(1.0 / (ii + 1.0)**3) H.AddMPOTerm('FiniteFunction', ['sz', 'sz'], f=f, hparam='J_z', weight=-1.0)generates
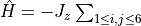
, where the summation is over all
and
pairs separated by at least
and at most
lattice spacings. The range of the potential is given by the number of elements in the list
f. This rule enforces Hermiticity and cares for Fermi phases as in the bond rule case.
InfiniteFunctionrule set (mpoterm.InfiniteFunc). We point out that this term is always fitted with a set ofmpoterm.ExpTermfor MPS simulations. Examples:
invrcube = lambda x: 1.0/(x*x*x) H.AddMPOTerm('InfiniteFunction', ['sz', 'sz'], hparam='J_z', weight=1.0, func=invrcube, L=1000, tol=1e-9)generates
, where the functional form is valid to a distance
Lwith a residual of at mosttol. Similarly,H.AddMPOTerm('InfiniteFunction', ['sz', 'sz'], hparam='J_z', weight=1.0, x=x, y=f, tol=1e-9)generates
, where the functional form
is determined by the array of values
fand the array of evaluation pointsx. The distance of validityLis determined from the arrayx. This rule applies only to monotonically decreasing functionsfuncorf, and so outside the range of validityLthe corrections are also monotonically decreasing. This rule enforces Hermiticity and cares for Fermi phases as in the bond rule case.
productrule (mpoterm.ProductTerm). Example:
H.AddMPOTerm('product', 'sz', hparam='h_p', weight=-1.0)generates
. The operator used in the product must be Hermitian.
MBStringrule set(mpoterm.MBStringTerm). See function description for usage.mpoterm.TTerm. See function description for usage.mpoterm.SiteLindXX. See function description for usage.mpoterm.LindExp. See function description for usage.mpoterm.LindInfFunc. See function description for usage.mpoterm.MBSLind. See function description for usage. (Can act as nearest neighbor Lindblad term.)
In all of the above expressions, H is an object of the MPO class.
The strings passed to the argument hparams represent tags for variable
Hamiltonian parameters, which allow for easy batching and parallelization
(Sec. Running a parallel static simulation), and also facilitate dynamical processes
The argument hparams is optional, and defaults to the constant
value 1. The optional argument weight specifies a constant factor that
scales the operator and defaults to the value 1, too.
Developer’s Guide for Rule Sets
Module contains a class for each possible term in the MPO rule sets. Each term is derived from a base class.If you plan to add additional MPO terms to OSMPS, you have to modify the following files. In the case of a new Lindblad operator, these are
mpoterm.py: add class for the new term
mpo.py: add new term to the MPO structure and enable writing.
MPOOps_types_templates.f90: define derived type and add to MPORuleSet
MPOOps_include.f90: add read/destroy methods for RuleSets
MPOOps_include.f90: effective Hamiltonian for 2 sites
MPOOps_include.f90: Liouville operator for 2 sites
MPOOps_include.f90: effective Hamiltonian represented as MPO.
MPOOps_include.f90: Liouville operator represented as MPO.
TimeevolutionOps_include.f90: Add overlaps to QT functionality.
- mpoterm._DecomposeOperator(Operator)[source]¶
Performs a singular value decomposition on a bond operator
![O_{[i j], [i' j']}](../_images/math/d59d928681c048e45640ad35a04edb92b077b17f.png) to find a Frobenius orthogonalized set
of operators
to find a Frobenius orthogonalized set
of operators 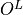 and
and 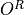 such that
such that
![O_{[i j], [i' j']} = \sum_a (O^L_a)_{i i'} (O^R_a)_{j j'}](../_images/math/e58cf26a5bdd737118c2043ce62291b104be99da.png) .
This allows us to only consider bond terms that are tensor products.
.
This allows us to only consider bond terms that are tensor products.Arguments
- Operator2d numpy array
Operator is represented as np 2d matrix of dimension
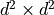 where
where 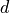 is the local dimenison
of one site in the Hilbert space.
is the local dimenison
of one site in the Hilbert space.
- mpoterm.DecomposeOperator(Operator, gen)[source]¶
Performs a singular value decomposition on a bond operator
![O_{[i j], [i' j']}](../_images/math/d59d928681c048e45640ad35a04edb92b077b17f.png) to find a Frobenius orthogonalized set
of operators
to find a Frobenius orthogonalized set
of operators 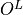 and
and 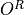 such that
such that
![O_{[i j], [i' j']} = \sum_a (O^L_a)_{i i'} (O^R_a)_{j j'}](../_images/math/e58cf26a5bdd737118c2043ce62291b104be99da.png) .
This allows us to only consider bond terms that are tensor products.
.
This allows us to only consider bond terms that are tensor products.Arguments
- Operator2d numpy array
Operator is represented as np 2d matrix of dimension
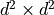 where
where 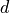 is the local dimenison
of one site in the Hilbert space.
is the local dimenison
of one site in the Hilbert space.- genlist of np 1d-arrays or
None Contains the diagonal entries of the diagonal symmetry generator for a two-site operator for each symmetry. If there are no symmetries, pass
None.
- mpoterm.fittoexpSum(x, y, maxnterms, tol)[source]¶
Fit a sum of exponentials
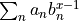 to the function
across the range [1:L].
to the function
across the range [1:L].Arguments
- x1d array
represents the points x where the function f(x) is evaluated and fitted.
- y1d array
Actual values of f(x) which should be represented by the sum of exponentials.
- intmaxnterms
the maximum number of exponentials allowed
- floattol
the tolerance used to obtain the actual number of terms.
- mpoterm.sumexp(p, x)[source]¶
Returns
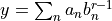 .
.Arguments
- p1d array
p is an array of length 2n with n pairs. The first entry of each pair is the coefficient
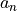 , the second entry of each
pair is the exponential decay value
, the second entry of each
pair is the exponential decay value 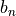 . For example
. For example
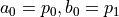 .
.- x1d array
contains the points x to evaluate the function f(x). Array is of some length l.
- mpoterm.hash_dict(dic)[source]¶
Generate the hash of a dictionary. Since the ordering of the entries of str(dic) is always different, we build pairs of keys and values and sort them alphabetical.
Arguments
- dicDictionary
get hash of this dictionary
Details
Nested structures might still lead to errors in this function. Dictionaries inside dic are solved by recursion calling hash_dict. List of dictionaries or similar structures do not consider the dictionaries inside the list properly.
- mpoterm.bose_einstein_stat(Ek, Te, kb, mu)[source]¶
Return probability according to Bose-Einstein statistics.
Arguments
- Ekfloat
Energy for requested probability.
- Tefloat
Temperature of the system.
- kbfloat
Boltzmann constant.
- mufloat
Chemical potential of the system.
- mpoterm.fermi_dirac_stat(Ek, Te, kb, mu)[source]¶
Return probability according to Bose-Einstein statistics.
Arguments
- Ekfloat
Energy for requested probability.
- Tefloat
Temperature of the system.
- kbfloat
Boltzmann constant.
- mufloat
Chemical potential of the system.
- class mpoterm._MPOTerm[source]¶
Abstract class providing general class methods for MPO terms.
The following class methods have to be provided for each new MPO term to work seemlessly inside of the whole rule set for MPS calculations:
__init__AddTermwriteprint_term(if it should appear in the printed equation of the Hamiltonian)
For calculations with the ED module inside openMPS the following class methods are necessary:
build_nosymmbuild_symm
- __getitem__(key)[source]¶
Return the class variable according to a string
Arguments
- keystr
Identifier string for class variable in MPO term.
- _col_ind_dic(Op)[source]¶
Create a dictionary taking a row index as key and returning the corresponding non-zero elements of the operators as tuple (column index, value).
Arguments
- Opnumpy 2d array
Operators to be transfered into this format.
- check_ti(params)[source]¶
Check if term is translational invariance. For translational invariance we check if the coupling have the attribute
__len__.Arguments
- paramsdictionary
The dictionary setting up a simulation. It coutains the couplings which are checked here.
- decompose(terms, phase, gen2)[source]¶
Run checks and iterate over decomposition of operators and their weight. Returns tuple (left Operators, right Operator, left weight, right weight).
Arguments
- termstr or 2d numpy array
Matrix acting on two sites, either in part of OperatorList or directly numpy 2d matrix.
- Phasebool
Flag for Fermi phase.
Details
Checks contain hermiticity of operator and no phase term.
- default(defargs, kwargs)[source]¶
Set the default arguments for a term if not passed as optional arguments in
AddTerm.- defargsdict
keywords and default value for default arguments. Only set if not present in
kwargs- kwargsdict
dictionary of keywords arguments as passed to
AddTerm
- get_sparse_dense_func(sparse, quenchtime)[source]¶
Set functions depending on sparse or dense structure of algorithms. The functions returned are the kronecker product, the identity, and the getting the operator.
Operators
- sparsebool
If true, sparse methods from
scipy.sparseare used, otherwise dense methods fromnumpy.- quenchtime
Noneor tuple For
Nonesparse matrices are incscformat, otherwise incsrformat. No effect on dense matrices.
- herm_conj_term(term0, term1)[source]¶
Check on the hermitian conjugated term and return parameters if existant as left operator, right operator, left weight * right weight.
Arguments
- term0str
string identifier for left term
- term1str
string identifier for right term
- hparam(ii, param, quenchtime)[source]¶
Return actual parameter as float for a term in the Hamiltonian multiplied with the weight.
Arguments
- iiint
index of the Hamiltonian parameter.
- paramdict
setup for the simulation. Contains information about couplings and dynamics.
- quenchtimeNone or tuple of int and float
For statics pass None. For dynamics pass integer ii for the ii-th quench and the actual time t as float in a tuple as (ii, t).
- ignored(optargs, kwargs)[source]¶
Print warnings about ignored optional keyword parameters:
Arguments
- optargslist of strings
contains all the string identifiers of the keyword arguments considered.
- kwargsdictionary
contains all the keywords arguments
- phased_herm_conj_term(PhasedR, term1)[source]¶
Generate the hermitian conjugated terms for a phased pair of operators. Return left operator, right operator, combined weight
Arguments
- PhasedRstr
string identifier for phased operator acting on the left site.
- term1str
string identifier for the operator acting on the right site.
- class mpoterm.SiteTerm(Operators)[source]¶
MPO rule set for site terms of the type
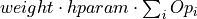 .
.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the string identifiers for the operators of the ii-th site term.
- weightlist
The ii-th float in the list contains the weight for the ii-th site term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th site term.
Details
To add a SiteTerm, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
site.- termsstr
string is the name of the operator acting locally on all sites.
- weightfloat, optional
Overall weight for the rule Default to 1.0.
- hparamstr, optional
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).
- AddTerm(terms, **kwargs)[source]¶
Add a new SiteTerm. For arguments see class description
mpoterm.SiteTerm.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Hamiltonian for a system without symmetries. This iterator return the matrix on the complete Hilbert space.
Arguments
- paramdictionary
dictionary with the setup for one simulation.
- sparsebool
Use sparse methods to build the whole Hamiltonian.
- quenchtime
Noneor tuple of integer, float If
None, access static coupling. If tuple, first entry contains the index of the quench, the second entry contains the time to evaluate the coupling.- llint
System size
- ldint
Local dimension for one site.
- pbcbool
used to identify periodic boundary conditions. If not referenced for the terms, *args is used.
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element.
Arguments
- paramdictionary
dictionary with the setup for one simulation.
- SymmSecinstance of
exactdiag.SymmetrySector Allows the mapping to the basis states according to the symmetry.
- quenchtime
Noneor tuple of integer, float If
None, access static coupling. If tuple, first entry contains the index of the quench, the second entry contains the time to evaluate the coupling.- llint
System size
- pbcbool
used to identify periodic boundary conditions. If not referenced for the terms, *args is used.
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for the fortran interface.
Arguments
- fhfilehandle
Open filehandle of file to write to.
- IntHparamdictionary
mapping the string identifiers for Hamiltonian parameters to integer identifiers used within fortran.
- IntOperatorsdictionary
mapping the string identifiers for the operators to integer identifiers used within fortran.
- Paramsdictionary
containing the parameters for one simulation
- Operatorsinstance of
- class mpoterm.BondTerm(Operators)[source]¶
Bond term
![weight \cdot hparam \cdot \sum_i Op[1]_i Op[2]_{i+1}](../_images/math/528c0294ed57c8b9c84ec6186887460ea925eddd.png) is added to the to the MPO. If Phase is present then
is added to the to the MPO. If Phase is present then
![\sum_i [ (Op[1]_i P) Op[2]_{i+1}+(P Op[1]_i^{\dagger})](../_images/math/a3688e418402df14072c9d013b87dee86d062fe9.png)
![Op[2]_{i+1}^{\dagger}]](../_images/math/c4ec241ee1b7bd1b91cf569cac5622b15634e963.png) is added. This routine will also add the Hermitian conjugate unless
both operators are their own hermitian conjugates. If only one operator
is passed then a decomposition request is assumed.
is added. This routine will also add the Hermitian conjugate unless
both operators are their own hermitian conjugates. If only one operator
is passed then a decomposition request is assumed.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th bond term.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th bond term.
Details
To add a BondTerm, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
bond.- termslist of str
strings are the name of the operators acting on all neighboring sites.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).- Phaseboolean (optional keyword argument)
Add a Fermi phase operator originating from the Jordan-Wigner transformation, e.g. for fermionic systems. Due to the Jordan-Wigner transformation, the order of the operator changes the Hamiltonian. The default order is of type
['fdagger', 'f']. Default to ``False.- gen2list of 1d np array or
None The diagonal entries of the diagonal symmetry generator of a two site operator used when decomposition request is made. Not referenced if two operators are passed to the bond term.
- AddTerm(terms, **kwargs)[source]¶
Add a new BondTerm. For arguments see class description
mpoterm.BondTerm.
- add(terms, weight, hparam)[source]¶
Adding BondTerm for internal use.
Arguments
- terms: list of two string
Two string identifiers for the operators as list.
- weight: float
Weight for the whole bond term.
- hparam: str
String identifier for the Hamiltonian parameter.
- build_nosymm(param, sparse, quenchtime, ll, ld, pbc)[source]¶
Build the Hamiltonian for a system without symmetries. This iterator return the matrix on the complete Hilbert space. For description of arguments look into
mpoterm.SiteTerm.build_nosymm().
- build_symm(param, SymmSec, quenchtime, ll, pbc)[source]¶
Build the Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm().
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.ExpTerm(Operators)[source]¶
Add an exponential term
![hparam \cdot \sum_{i<j} Operators[0]_i](../_images/math/3e0b295000bf28eecb387fbbfff7913a5b450644.png)
![Operators[1]_j decayparam^{j-i-1}](../_images/math/c7a6dc51173f1ee63d20ef7b518a2cbe22798e7f.png) to the MPO. If only one
operator is passed then a decomposition request is assumed.
to the MPO. If only one
operator is passed then a decomposition request is assumed.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th FiniteFunc term.
- weightlist
The ii-th float in the list contains the weight for the ii-th FiniteFunc term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th FiniteFunc term.
- dplist of floats
List of the strenght of the exponential decays of the ii-th term.
Details
To add a ExpTerm, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
exponential.- termslist of str
strings are the name of the operators acting on all neighboring sites.
- decayparamfloat (keyword argument)
configuring the decay as 1 / decayparam**d where d is the distance.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).- Phaseboolean (optional keyword argument)
Add a Fermi phase operator originating from the Jordan-Wigner transformation, e.g. for fermionic systems. Due to the Jordan-Wigner transformation, the order of the operator changes the Hamiltonian. The default order is of type
['fdagger', 'f']. Default to ``False.
- AddTerm(terms, **kwargs)[source]¶
Add a new ExpTerm. For arguments see class description
mpoterm.ExpTerm.
- add(terms, weight, hparam, decayparam)[source]¶
Adding ExpTerm for internal use.
Arguments
- terms: list of three string
Two string identifiers for the operators as list.
- weight: float
Weight for the whole bond term.
- hparam: str
String identifier for the Hamiltonian parameter.
- decayparamfloat
Decay parameter of the exponential rule.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Hamiltonian for a system without symmetries. This iterator return the matrix on the complete Hilbert space. For description of arguments look into
mpoterm.SiteTerm.build_nosymm().
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm().
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.FiniteFunc(Operators)[source]¶
Add a FiniteFunction term
![weight \cdot hparam \cdot \sum_{i,j<=r_c} f[i-j] Op[1]_i Op[2]_{j}](../_images/math/6fbd3d4988d64a15e332df8d4d8dc5be9599d141.png) to the MPO. If only one operator is passed then a decomposition request
is assumed.
to the MPO. If only one operator is passed then a decomposition request
is assumed.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th FiniteFunc term.
- weightlist
The ii-th float in the list contains the weight for the ii-th FiniteFunc term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th FiniteFunc term.
- flist of 1d vectors
List of coupling up to the specified range.
- r_clist of ints
Range of the ii-th FiniteFunc term.
- Phaselist of strings
List of the phase operator inbetween the left and right operator. This is the identity
'I'if no phase present.
Details
To add a FiniteFunc term, you have to pass the following arguments to
mpo.MPO.AddMPOTerm()- termtypestr
String must be equal to
FiniteFunc.- termsstr
string is the name of the operator acting locally on all sites.
- f1d array (keyword argument)
Containing the weight for a with distance for a range specified through the length of the array.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).- Phaseboolean (optional keyword argument)
Add a Fermi phase operator originating from the Jordan-Wigner transformation, e.g. for fermionic systems. Due to the Jordan-Wigner transformation, the order of the operator changes the Hamiltonian. The default order is of type
['fdagger', 'f']. Default to ``False.
- AddTerm(terms, **kwargs)[source]¶
Add a new FiniteFunc term. For arguments see class description
mpoterm.FiniteFunc.
- add(terms, weight, hparam, farray, Phase)[source]¶
Adding FiniteFunc term for internal use.
Arguments
- terms: list of two string
Two string identifiers for the operators as list.
- weight: float
Weight for the whole bond term.
- hparam: str
String identifier for the Hamiltonian parameter.
- farray1d vector
Coupling as a function of distance. Specifies the range through the length of the array.
- Phasestr
String identifier for the phase operator.
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.InfiniteFunc(Operators, ExpTermMPO, PostProcess)[source]¶
Add a term to the Hamiltonian
![weight \cdot hparam \cdot \sum_{i<j} f(i-j) Operators[0]_i](../_images/math/66424054a1e5346edc4dc0b56493a8168f5fb2c7.png)
![Operators[1]_j](../_images/math/4be897e9090d94b0bc393139d75f6ba8fbd7e6e4.png) where
where 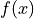 is specified as a function
handle on input. This is done by finding the series of weighted
exponentials
is specified as a function
handle on input. This is done by finding the series of weighted
exponentials 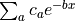 which best approximates this function and then adding those terms to
the exponential part of the MPO. If only one operator is passed then a
decomposition request is assumed.
which best approximates this function and then adding those terms to
the exponential part of the MPO. If only one operator is passed then a
decomposition request is assumed.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
- ExpTermMPOinstance of
mpoterm.ExpTerm Add the fitted exponential terms to this instance of a class.
- PostProcessbool
If
Truethe functions are not fitted. IfFalsefitting procedure expresses InfiniteFunc as ExpTerms.
Variables
- etmpoinstance of
mpoterm.ExpTerm Add the fitted exponential terms to this instance of a class. Passed to
__init__asExpTermMPO.- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th bond term.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th bond term.
- yvalslist of vectors
The ii-th vector specifies the coupling with distance.
Details
To add a InfiniteFunc term, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
InfiniteFunction.- termslist of str
strings are the name of the operators acting on all neighboring sites.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).- Phaseboolean (optional keyword argument)
Add a Fermi phase operator originating from the Jordan-Wigner transformation, e.g. for fermionic systems. Due to the Jordan-Wigner transformation, the order of the operator changes the Hamiltonian. The default order is of type
['fdagger', 'f']. Default to ``False.- maxntermsint (optional keyword argument)
Number of exponentials maximally allowed to fit InfiniteFunction Default to 16.
- tolfloat (optional keyword argument)
This sets the tolerance for the fit of the infinite function with the exponentials. Default to 1e-6
- funccallable (optional keyword argument)
Function returning the coupling as a function for the distance. Combined with the argument
L, it may be used to specify the InfiniteFunction Default toNone- Lint (optional keyword argument)
range for fitting the exponentials to the function
funcDefault toNone- x1d vector (optional keyword argument)
The values of the function to be fitted can be given as two vector x and y = f(x). These are the x-values. Default to
None- y1d vector (optional keyword argument)
The values of the function to be fitted can be given as two vector x and y = f(x). These are values of the function. Default to
None- EDbool (optional keyword argument)
It can only be used to indicate for the EDLib not to fit an InfiniteFunction with exponentials. Default to
False
Although func, L, x, y are all marked as optional, either x and y or func and L have to be provided.
- AddTerm(terms, **kwargs)[source]¶
Add a new InfiniteFunc. For arguments see class description
mpoterm.InfiniteFunc.
- AddTermED(terms, weight, hparam, Phase, xval, yval)[source]¶
For the exact diagonlization code we can use the infinite functions directly.
Arguments
- terms: list of two string
Two string identifiers for the operators as list.
- weight: float
Weight for the whole bond term.
- hparam: str
String identifier for the Hamiltonian parameter.
- Phasestr
String identifier for the phase operator.
- xval1d vector
values with the x-coordinates for the yval = f(xvals). Has to start at 1 and have an increment 1.
- yval1d vector
Values with the distance dependent couplting.
- add(terms, weight, hparam, yval)[source]¶
Add InfiniteFunc term, internal use only.
Arguments
- terms: list of two string
Three string identifiers for the operators as list. Order is left operator, right operator, phase operator.
- weight: float
Weight for the whole bond term.
- hparam: str
String identifier for the Hamiltonian parameter.
- yval1d vector
Values with the distance dependent couplting.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Hamiltonian for a system without symmetries. This iterator return the matrix on the complete Hilbert space. For description of arguments look into
mpoterm.SiteTerm.build_nosymm().
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm().
- Operatorsinstance of
- class mpoterm.ProductTerm(Operators)[source]¶
Add a product term
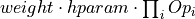 to the MPO.
to the MPO.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th bond term.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th bond term.
Details
To add a ProductTerm, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
product.- termsstr
String identifier for the operator.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).
- AddTerm(terms, **kwargs)[source]¶
Add a new BondTerm. For arguments see class description
mpoterm.ProductTerm.
- write(fh, IntHparams, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.MBStringTerm(Operators)[source]¶
Add a many-body string term
![weight \cdot hparam \cdot \sum_i \prod_{j=1}^{n} Op[j]_{i+j-1}](../_images/math/bc66ae7bc95685621608a87c1249af48c0136af8.png) to the MPO, where Op[j] is the
to the MPO, where Op[j] is the 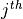 element of term. The number
of such operators n is determined from the length of the input list.
This routine does not check for Hermiticity.
element of term. The number
of such operators n is determined from the length of the input list.
This routine does not check for Hermiticity.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th bond term.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th bond term.
Details
To add a MBStringTerm, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
MBString.- termslist of str
String identifiers for the string of operators.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).
- AddTerm(terms, **kwargs)[source]¶
Add a new MBString term. For arguments see class description
mpoterm.MBStringTerm.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Hamiltonian for a system without symmetries. This iterator return the matrix on the complete Hilbert space. For description of arguments look into
mpoterm.SiteTerm.build_nosymm().
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm().
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.TTerm(Operators)[source]¶
MPO rule for a site 1 to k-1 interaction with site k. The interaction strength is independent of the distance.
Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th bond term.
- kklist of ints
The ii-th entry contains the site which sites 1 .. (kk - 1) are interacting to for the ii-th rule.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th bond term.
Details
To add an TTerm you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
must be
ttermto add this term.- termslist of two strings
strings are the names of the operators acting on the sites 1 to k-1 (first string) and the site k (second string).
- kkint (keyword argument)
All sites left of site kk interact with site k. Indexing NOT in python standard starting from 0, but from 1.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).
- AddTerm(terms, **kwargs)[source]¶
Add a new TTerm. For arguments see class description
mpoterm.TTerm
- add(terms, kk, weight, hparam)[source]¶
Adding TTerm for internal use.
Arguments
- terms: list of two string
Two string identifiers for the operators as list.
- kkint
All sites left of site kk interact with site k.
- weight: float
Weight for the whole bond term.
- hparam: str
String identifier for the Hamiltonian parameter.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Hamiltonian for a system without symmetries. This iterator returns the matrix on the complete Hilbert space. For description of arguments look into :py:func:mpoterm.SiteTerm.build_nosymm`.
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm(). NOT IMPLEMENTED.
- check_ti(*args)[source]¶
TTerms are by default not translational invariant since they depend on site kk.
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.SiteLindXX(Operators)[source]¶
Add a Lindblad term
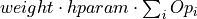 to the MPO.
to the MPO.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th bond term.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th bond term.
Details
To add a single site Lindblad channel, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termstring
string name of the operator
- weightfloat, optional
general weight, e.g. a minus sign
- hparamstring, optional
possibly site and time dependent coupling default to ‘one’
- AddTerm(terms, **kwargs)[source]¶
Add a new SiteLindXX. For arguments see class description
mpoterm.SiteLindXX.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the effective Hamiltonian for a system without symmetries. This iterator return the matrix on the complete Hilbert space. For description of arguments look into
mpoterm.SiteTerm.build_nosymm().
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the effective Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm().
- lbuild_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Liouville operator for a system without symmetries. This iterators returns the matrix build on the complete Liouville space.
Arguments
- paramdictionary
dictionary with the setup for one simulation.
- sparsebool
Use sparse methods to build the whole Hamiltonian.
- quenchtime
Noneor tuple of integer, float If
None, access static coupling. If tuple, first entry contains the index of the quench, the second entry contains the time to evaluate the coupling.- llint
System size
- ldint
Local dimension for one site.
- pbcbool
used to identify periodic boundary conditions. If not referenced for the terms, *args is used.
- lbuild_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Liouville operator for a system with symmetries. This iterator returns a tuple of the row index, column index in the Liouville space, and value of the matrix element.
Arguments
- paramdictionary
dictionary with the setup for one simulation.
- SymmSecinstance of
exactdiag.SymmetrySector Allows the mapping to the basis states according to the symmetry.
- quenchtime
Noneor tuple of integer, float If
None, access static coupling. If tuple, first entry contains the index of the quench, the second entry contains the time to evaluate the coupling.- llint
System size
- pbcbool
used to identify periodic boundary conditions. If not referenced for the terms, *args is used.
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.MBSLind(Operators)[source]¶
Add a many-body string Lindblad
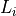 operator defined as
operator defined as
![L_i = weight \cdot hparam \cdot \prod_{j=1}^{n} Op[j]_{i+j-1}](../_images/math/bafd990bccb5f9d10f69305d55997b66fb413bed.png) acting on every sequence of
acting on every sequence of 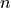 neighboring sites. The number
of operators is determined from the length of the input list.
neighboring sites. The number
of operators is determined from the length of the input list.Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The ii-th entry contains the n string identifiers for the n operators of the ii-th bond term.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th Lindblad term.
Details
To add a MBSLind, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
MBSLind.- termslist of str
String identifiers for the string of operators.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).
- AddTerm(terms, **kwargs)[source]¶
Add a new MBSLind term. For arguments see class description
mpoterm.MBSLind.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the effective hamiltonian for a system without symmetries. This iterator returns the matrix on the complete Hilbert space for the effective Hamiltonian. For description of terms look into
mpoterm.SiteTerm.build_nosymm().
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the effective Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm(). NOT IMPLEMENTED.
- lbuild_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Liouville operator for a system without symmetries. This iterator returns the matrix build on the complete Liouville space. Arguments see
mpoterm.SiteLindXX.lbuild_nosymm().
- lbuild_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Liouville operator for a system with symmetries. This iterators returns a tuple of the row index, column index in the Liouville space, and value of the matrix element. NOT IMPLEMENTED.
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.MBSLindXY(Operators)[source]¶
Add a many-body string Lindblad with different arguments for L and Ldagger.
Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
Variables
- Oplist
The length of the list is
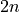 , where the Lindblad
operator spans n sites. The ii-th and the (n + ii)-th
string of the list define the operators acting on the
ii-th site of the Lindblad operator as L and Ldagger,
respectively.
, where the Lindblad
operator spans n sites. The ii-th and the (n + ii)-th
string of the list define the operators acting on the
ii-th site of the Lindblad operator as L and Ldagger,
respectively.- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th Lindblad term.
Details
To add a MBSLind, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
MBSLindXY.- termslist of str
String identifiers for the string of operators.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).
- AddTerm(terms, **kwargs)[source]¶
Add a new MBSLindXY term. For arguments see class description
mpoterm.MBSLindXY.
- build_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the effective hamiltonian for a system without symmetries. This iterator returns the matrix on the complete Hilbert space for the effective Hamiltonian. For description of terms look into
mpoterm.SiteTerm.build_nosymm().
- build_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the effective Hamiltonian for a system with symmetries. This iterator returns a tuple of the row index, column index, and value of the matrix element. For complete description look into
mpoterm.SiteTerm.build_symm(). NOT IMPLEMENTED.
- lbuild_nosymm(param, sparse, quenchtime, ll, ld, *args)[source]¶
Build the Liouville operator for a system without symmetries. This iterator returns the matrix build on the complete Liouville space. Arguments see
mpoterm.SiteLindXX.lbuild_nosymm().
- lbuild_symm(param, SymmSec, quenchtime, ll, *args)[source]¶
Build the Liouville operator for a system with symmetries. This iterators returns a tuple of the row index, column index in the Liouville space, and value of the matrix element. NOT IMPLEMENTED.
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- Operatorsinstance of
- class mpoterm.LindExp(Operators)[source]¶
Add a Lindblad term with and exponential decay of the interaction in distance between the two sites
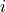 and
and 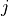 as
as
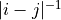 .
.Arguments
Variables
Details
To add a LindExp term, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
LindExp- termslist of str
String identifiers for the operators acting on the left and on the right site.
- decayparamfloat (keyword argument)
Configuring the decay as 1 / decayparam**d where d is the distance.
- weightfloat (optional keywork argument)
Overall weight for the rule. Default to 1.0
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).- StringOpstr (optional keyword argument)
Possibility to add operator acting on all sites between the left and the right site. This can be used for a Fermi phase or similar operations (If string is equal to
FermiPhase, correct operators for left and right site are constructed.) Default to Identity (I).
- AddTerm(terms, **kwargs)[source]¶
Add a new LindExp term. For arguments see class description
mpoterm.LindExp.
- add(terms, weight, hparam, decayparam)[source]¶
Add LindExp for internal use.
Arguments
- terms: list of three string
Two string identifiers for the operators as list.
- weight: float
Weight for the whole bond term.
- hparam: str
String identifier for the Hamiltonian parameter.
- decayparamfloat
Decay parameter of the exponential rule.
- write(fh, IntHparam, IntOperators, Params)[source]¶
Write the information for fortran interfaces. For description of arguments see
mpoterm.SiteTerm.write().
- class mpoterm.LindInfFunc(Operators, ExpTermMPO, PostProcess)[source]¶
Add Lindblad operators acting on two sites where the coupling is decaying with increasing distance between the sites.
Arguments
- Operatorsinstance of
Ops.OperatorList the operators on the local Hilbert space used.
- ExpTermMPOinstance of
mpoterm.ExpTerm Add the fitted exponential terms to this instance of a class.
- PostProcessbool
If
Truethe functions are not fitted. IfFalsefitting procedure expresses InfiniteFunc as ExpTerms.
Variables
- etmpoinstance of
mpoterm.ExpTerm Add the fitted exponential terms to this instance of a class. Passed to
__init__asExpTermMPO.- Oplist
The ii-th entry contains the two string identifiers for the left and right operators of the ii-th bond term.
- weightlist
The ii-th float in the list contains the weight for the ii-th bond term.
- hplist
The ii-th string in the list contains links to the Hamiltonian paramater with the coupling used for the ii-th bond term.
- yvalslist of vectors
The ii-th vector specifies the coupling with distance.
Details
To add a InfiniteFunc term, you have to pass the following arguments to
mpo.MPO.AddMPOTerm():- termtypestr
String must be equal to
InfiniteFunction.- termslist of str
strings are the name of the operators acting on all neighboring sites.
- weightfloat (optional keyword argument)
Overall weight for the rule Default to 1.0.
- hparamstr (optional keyword argument)
String identifying the Hamiltonian parameters allowing for quenching the parameter or changing it for different static simulations. Default to 1.0 (
one).- StringOpstr (optional keyword argument)
Possibility to add operator acting on all sites between the left and the right site. This can be used for a Fermi phase or similar operations (If string is equal to
FermiPhase, correct operators for left and right site are constructed.) Default to Identity (I).- maxntermsint (optional keyword argument)
Number of exponentials maximally allowed to fit InfiniteFunction Default to 16.
- tolfloat (optional keyword argument)
This sets the tolerance for the fit of the infinite function with the exponentials. Default to 1e-6
- funccallable (optional keyword argument)
Function returning the coupling as a function for the distance. Combined with the argument
L, it may be used to specify the InfiniteFunction Default toNone- Lint (optional keyword argument)
range for fitting the exponentials to the function
funcDefault toNone- x1d vector (optional keyword argument)
The values of the function to be fitted can be given as two vector x and y = f(x). These are the x-values. Default to
None- y1d vector (optional keyword argument)
The values of the function to be fitted can be given as two vector x and y = f(x). These are values of the function. Default to
None- EDbool (optional keyword argument)
It can only be used to indicate for the EDLib not to fit an InfiniteFunction with exponentials. Default to
False
Although func, L, x, y are all marked as optional, either x and y or func and L have to be provided.
- AddTerm(terms, **kwargs)[source]¶
Add a new Lindblad infinite function terms. For arguments see class description
mpoterm.LindInfFunc.
- Operatorsinstance of
- class mpoterm.LindLSpec(Operators)[source]¶
Add Lindblad term based on the spectral decomposition of a small subsystem. In contrast to the
mpoterm.LindSpecthis approach is not based on a operator.- AddTerm(terms, **kwargs)[source]¶
Add Lindblad operators based on a spectral decomposition of a subpart of the system. For arguments see class description of
mpoterm.LindLSpec.
- build_nosymm(param, sparse, quenchtime, ll, ld, Ham)[source]¶
Build the effective Hamiltonian for a system without symmetries This iterator returns the matrix on the complete Hilbert space.
Arguments
- Haminstance of
mpo.MPO Represents the MPO of the full system. At present couplings must be translational invariant.
- Haminstance of
- get_transitions(locparam, locham, quenchtime, ll, ld, pbc)[source]¶
Construct the transition Lindblad operators.
- lbuild_nosymm(param, sparse, quenchtime, ll, ld, Ham)[source]¶
Build the Liouville operator for a system without symmetries This iterator returns the matrix built on the complete Liouville space. Arguments see
mpoterm.SiteLindXX.lbuild_nosymm().- Haminstance of
mpo.MPO Represents the MPO of the full system. At present couplings must be translational invariant.
- Haminstance of
- class mpoterm.LindSpec(Operators)[source]¶
Add Lindblad terms for reservoirs based on the spectral decomposition.
Arguments
- weightfloat
General weight. Default to 1.0
- hparamstr
That is the coupling of the operator to the field in the reservoir given as
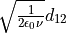 .
Each non-zero coupling means a coupling to the same
reservoir. The term is squared for translational invariant
coupling and multiplied as
.
Each non-zero coupling means a coupling to the same
reservoir. The term is squared for translational invariant
coupling and multiplied as ![g[i] \cdot g[j]](../_images/math/e9ee82ff5e96b985bccc007b5b254499853a5787.png) if acting
on sites i and j.
Default to
if acting
on sites i and j.
Default to one.- Testr or float
Temperature of the reservoir. If str, the corresponding key must be in the simulation dictionary. Default to 0.0
- Tapproxtuple of (float, int, int)
Tolerance and minimal and maximal number of transitions. If ints are None, maximal number of terms is assumed. Default to (1e-15, None, None)
- wtolfloat
Tolerance for truncating a transition times
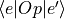 .
Default to 1e-15
.
Default to 1e-15- ctolfloat
Tolerance for truncating a whole term. Default to 1e-15
- kbstr or float
Boltzmann constant. If str, the corresponding key must be in the simulation dictionary. Default to 1.0
- mustr or float
Chemical potential. If str, the corresponding key must be in the simulation dictionary. Default to 0.0
- alstr or float
Lattice constant or distance between sites. The sites are assumed to be equidistant. If str, the corresponding key must be in the simulation dictionary. Default to 1.0
- ccstr or float
Speed of light. If str, the corresponding key must be in the simulation dictionary. Default to 1.0
- pvtablebool or instance of Interpol
If False, no principal value is used and thus there is no effective Hamiltonian. If True, principal value part is used, but no table is given. If pvtable is not of type bool, it is assumed that an instance of Interpol is passed. Default to True.
- AddTerm(terms, **kwargs)[source]¶
Add Lindblad operators based on a spectral decomposition. For arguments see class description of
mpoterm.LindSpec.
- _get_lindblads_both(param, quenchtime, ll, Ham, ld=None, SymmSec=None)[source]¶
Generate all Lindblad operators from the spectral decomposition.
- build_nosymm(param, sparse, quenchtime, ll, ld, Ham)[source]¶
Build the effective Hamiltonian for a system without symmetries. This iterator returns the matrix on the complete Hilbert space.
Arguments
- get_lindblads_nosymm(param, quenchtime, ll, ld, Ham)[source]¶
Generate all Lindblad operators from the spectral decomposition.
- get_lindblads_symm(param, SymmSec, quenchtime, ll, Ham)[source]¶
Generate all Lindblad operators from the spectral decomposition.
- lbuild_nosymm(param, sparse, quenchtime, ll, ld, Ham)[source]¶
Build the Liouville operator for a system without symmetries. This iterator returns the matrix build on the complete Liouville space.
Arguments
- Ham2d matrix
The Hamiltonian represented as matrix or sparse matrix. (Not the rule set of the Hamiltonian.)
- select_eigenstates(param, Ham, ii_)[source]¶
Diagonalize the Hamiltonian and truncate high energy states if desired.
- select_transitions_nosymm(param, ld, ll, vals, vecs, nn, oo)[source]¶
Get the transitions energies between all selected eigenstates. The returned dictionary has the a tuple of two indices of the two corresponding eigenstates as key. The value of dictionary are two list containing the site indices and the weight.
Arguments
- ooint
Choose the oo-th term of Lindblad operators.
- select_transitions_symm(param, SymmSec, ll, vals, vecs, nn, oo)[source]¶
Get the transition energies between all selected eigenstates. The returned dicitionary has a tuple of two indices of the two corresponding eigenstates as key. The value of the dictionary are two lists containing the site indices and the weight.
- ooint
Choose the oo-th term of Lindblad operators.
- mpoterm._append2nparray(flnm, val)[source]¶
Append a value to a numpy array on the hard disk. Intend for debugging.
Arguments
- flnmstr
Filename is existing numpy array and will be updated with the additional entry.
- valfloat
Value to be appended to the numpy array.