Developer’s Manual¶
Programming conventions¶
Fortran¶
Indentation is 4 spaces, not tabs. This can be set in your editor.
IMPLICIT NONEis to be used in every Fortran scoping unit.PRIVATEshould be declared within each module, and only those data which need to be available to other modules should be separately declared asPUBLIC.The
USE module, only:syntax of including only what is necessary from other modules should be used to avoid polluting the namespace.The double precision variables should be declared as
REAL(KIND=rKind)for maximum portability.Generic programming is to be used as much as is reasonable using the strategy outlined in Sec. Generic programming in fortran with templates.
Every loop/if statement in Fortran should be indented.
All Fortran code should be standard conforming and compile using the compilers listed in the manual.
Do not use single-character variable names. Derived types should be capitalized, other variables lower case.
Python¶
Indentation is 4 spaces, not tabs. This can be set in your editor.
All routines and modules should have a meaningful docstring.
Generic programming in fortran with templates¶
One of the major drawbacks of programming in Fortran is that it does not
have a templating capability, which is the ability of procedures and
structures to operate with generic types. Thus, to create an operation
scale which scales either real or complex vectors by a real scalar would
require the following code stored in a module scale_module.f90:
MODULE scale_module
USE GlobalOps, only: rKind
IMPLICIT NONE
PRIVATE
TYPE Vector
REAL(KIND=rKind), POINTER :: d(:)
END TYPE Vector
TYPE CVector
COMPLEX(KIND=rKind), POINTER :: d(:)
END TYPE CVector
PUBLIC :: scale
INTERFACE scale
MODULE PROCEDURE :: scale_Vector, scale_CVector
END INTERFACE scale
CONTAINS
SUBROUTINE scale_Vector(a,v)
TYPE(Vector) :: v
REAL(KIND=rKind) :: a
v%d=a*v%d
END SUBROUTINE scale_Vector
SUBROUTINE scale_CVector(a,v)
TYPE(CVector) :: v
REAL(KIND=rKind) :: a
v%d=a*v%d
END SUBROUTINE scale_CVector
END MODULE
That is, we essentially have to copy the code twice with only changes to the
inputs. This makes the code harder to maintain, and opens up room for
type-dependent errors. In MPSFortLib, we have developed a strategy of template
programming in Fortran which uses the regex module of Python dealing
with regular expressions to build Fortran code from a set of templates. As an
example, the module scale_module.f90 above would be replaced by three files.
The first would contain a generic template for the vector types, call it
scale_types_template.f90:
!!TDic RESET
!!TDic REAL_OR_COMPLEX : real; complex
!!TDic VECTOR_TYPE : vector; cvector
TYPE VECTOR_TYPE
REAL_OR_COMPLEX(KIND=rKind), POINTER :: d(:)
END TYPE VECTOR_TYPE
Also, a file scale_include.f90 which performs the scaling operation on a
VECTOR_TYPE
!!TDic RESET
!!TDic REAL_OR_COMPLEX : real; complex
!!TDic VECTOR_TYPE : vector; cvector
subroutine scale_VECTOR_TYPE(a,v)
type(VECTOR_TYPE) :: v
real(KIND=rKind) :: a
v%d=a*v%d
end subroutine scale_VECTOR_TYPE
!PUBLIC_INTERFACE_scale&VECTOR_TYPE
And finally a file scale_template.f90 which instructs how to build
scale_module.f90 from these template files:
MODULE scale_module
USE GlobalOps, only: rKind
IMPLICIT NONE
PRIVATE
INCLUDE_TYPES
INCLUDE_PUBLICINTERFACES
CONTAINS
INCLUDE_FILES
END MODULE scale_module
The module scale_module.f90 is built from these three files using our
Python code. The Template dictionary (TDic) is defined in front of each
type and subroutine after cleaning (!!TDic RESET) it up from previous
calls. The word before the colon (:) is the key word to be replaced.
The ii-th entry of each line after the color will be used together in the
subroutine or function. They are separated by semi-colons. The number of
entries after the color specifies the number of subroutines.
The name of a public interface is specified after the subroutine. The
name of the interface is before the ampersand &. If the procedure
should be public, the statement !PUBLIC_PROCEDURE_scale_VECTOR_TYPE
can be added after the subroutine.
This approach allows to use different rules within in template file, which increases the flexibility a bit in comparison to previous version of OSMPS (v1 and v2).
Global keywords always available are
!CHECK_: will disable checks when optimization is choosen.IFMPI_: enabled when compiling with mpif90. In addition, there are templates for all MPI subroutines.IFIMPS_andIFNOIMPS_: will enable (disable) code depending on if iMPS should be compiled or not. Not compiling iMPS drops the dependency on ARPACK.IFMACACC_andIFNOTMACACC_: Switch between usage of Mac OS X accelerate package and other operating systems. Right now used to avoid segfaults in BLAS implementation of accelerate package.
For a detailed picture of the regex handling inside Python, please look into …
While all of this machinery is certainly overkill for the scale example
above, the nice feature is that the same code scales to an arbitrary number of
generic procedures within a module. In the long run, the amount of code and
the possibility for errors in duplication is much less.
Building this documentation¶
This documentation can be build using sphinx, i.e., the standard tool to generate most python documentations. Follow the following steps:
Build the OSMPS library. The documenation will access the fortran modules generated during compilation.
Change to the folder Documenation and run
make htmlTo update the documenation in
HTMLDocu, just run a recursive copycp -r build/html HTMPDocu. This is the folder linked to when building OSMPS.If you want to update the documentation tracked in the version control, run
python3 packdocu.py. Then add and commit to the version control.
Building the local Hilbert space and operators¶
How MPSPyLib builds Hilbert spaces¶
To discuss how MPSPyLib builds Hilbert spaces, it is first useful to discuss
the notion of lexicographic order. Consider the set
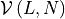 of vectors with
of vectors with 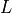 integer-valued
elements with values from
integer-valued
elements with values from  to
to 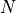 such that the sum of the
elements of the vector is fixed to be
such that the sum of the
elements of the vector is fixed to be 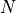 ,
, 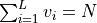 .
Take two vectors
.
Take two vectors 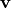 and
and 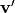 from this set
fulfilling the property that
from this set
fulfilling the property that 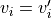 if
if 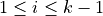 and
and
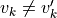 for some
for some 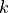 . We say that
. We say that 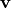 is
superior to
is
superior to 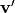 if
if 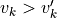 and that it is inferior
to
and that it is inferior
to 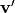 otherwise. Clearly,
otherwise. Clearly,
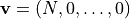 is superior to all other vectors
and
is superior to all other vectors
and 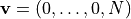 is inferior to all other
vectors. Given a vector
is inferior to all other
vectors. Given a vector 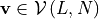 , one
finds the next inferior vector in
, one
finds the next inferior vector in 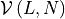 by the
following algorithm.
by the
following algorithm.
If the last element is
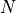 then there are no inferior vectors. Exit.
then there are no inferior vectors. Exit.Find the last
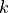 such that
such that 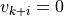 for all
for all
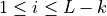 .
.Set
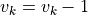 ,
, 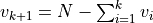 , and
, and
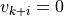 for all
for all 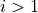 .
.
This is the purpose of the function Ops.steplexVec().
Thus, all elements in the set 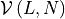 may be
generated by starting with the completely superior vector
may be
generated by starting with the completely superior vector
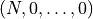 and using the above algorithm to generate
all other vectors. Other constraints on the minimum or maximum values of the
elements of
and using the above algorithm to generate
all other vectors. Other constraints on the minimum or maximum values of the
elements of 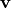 are easy to enforce by generating all vectors
and checking them individually for the desired properties, and the constraint
that the sum be exactly
are easy to enforce by generating all vectors
and checking them individually for the desired properties, and the constraint
that the sum be exactly 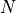 can be relaxed by using the algorithm for a
range of
can be relaxed by using the algorithm for a
range of 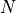 and adding the spaces in a direct sum. While more efficient
algorithms for indexing a Hilbert space may be devised, in MPSPyLib we only
build the Hilbert spaces consisting of a single site, and these do not have
large dimensionality.
and adding the spaces in a direct sum. While more efficient
algorithms for indexing a Hilbert space may be devised, in MPSPyLib we only
build the Hilbert spaces consisting of a single site, and these do not have
large dimensionality.
Symmetry-adapted operators¶
A symmetry-adapted operator is specified as
(10)¶![\hat{O}&=\bigoplus_{\mathbf{q}}\left[\hat{O}_{\mathbf{q}+\Delta \mathbf{q},\mathbf{q}}\right]_{t_{\mathbf{q}+\Delta \mathbf{q}}t_{\mathbf{q}}}\, ,](../_images/math/4fd934b6d153aa3d9b1fb138aba369d8a424f747.png)
where 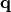 is the vector of Abelian charges specifying an irrep,
is the vector of Abelian charges specifying an irrep,
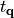 is an index running over the degeneracy dimension of
irrep
is an index running over the degeneracy dimension of
irrep 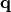 , and
, and 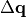 specifies how the
operator transforms under the group operation. The definition Eq. (10)
assumes that all operators transform covariantly with the group operation.
MPSPyLib can not (rather, will not) handle operators which do not transform
covariantly. A symmetry-conserving simulation can always be expressed in terms
of only covariant operators, and the use of only covariant operators simplifies
the numerical implementation and improves its efficiency.
specifies how the
operator transforms under the group operation. The definition Eq. (10)
assumes that all operators transform covariantly with the group operation.
MPSPyLib can not (rather, will not) handle operators which do not transform
covariantly. A symmetry-conserving simulation can always be expressed in terms
of only covariant operators, and the use of only covariant operators simplifies
the numerical implementation and improves its efficiency.
The transformation from operators to their symmetry-adapted counterparts is
accomplished with the function named
Ops.OperatorList.OperatorstoQOperators(). This
function operates with a set of operators expressed as a Python dictionary
self.Operators and a matrix or list of generators Generators which are
the tags of diagonal matrices whose elements are the charges of the Abelian
groups. Since we deal with finite representations, all of the charges can be put
into one-to-one correspondence with some subset of the positive integers. This
is accomplished by finding a shift 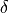 for each generator such that the
minimum charge is zero and a scaling factor
for each generator such that the
minimum charge is zero and a scaling factor 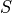 such that the minimum
difference between charges is an integer. That is, we have
such that the minimum
difference between charges is an integer. That is, we have
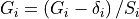
for each generator 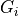 . The diagonal elements of these new generators
define the set of irreps
. The diagonal elements of these new generators
define the set of irreps 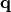 , which are sorted to find the
associated degeneracy dimensions. All other operators are transformed to this
sorted basis. These new operators are stored as a dictionary whose elements are
also dictionaries. The keys of the dictionary for a given operator are
, which are sorted to find the
associated degeneracy dimensions. All other operators are transformed to this
sorted basis. These new operators are stored as a dictionary whose elements are
also dictionaries. The keys of the dictionary for a given operator are 'q',
a list whose elements are lists of tuples specifying the incoming and outgoing
quantum numbers, and 'Blocks', a list of NumPy arrays specifying the action
of the operator within the degeneracy space of the specified irrep. In addition,
the operator dictionary has as keys 'q_numbers', a list of the irreps of
the Hilbert space; 'q_d', a dictionary mapping the irreps to their
degeneracy dimensions, 'nqns', the number of Abelian symmetries (i.e. the
length of the vector 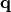 );
); 'q_shifts', the shifts
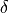 ;
; 'q_scales' the scale factors 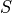 ; and
; and
'transformation' the matrix transforming the original basis to the
symmetry-adapted basis.
Function/Subroutine documentations¶
The remaining part of the documentation contains the description of all fortran functions and subroutines as far as available. Type definition or interfaces are not considered yet.