iMPSOps¶
Fortran module iMPSOps:Containing the methods for iMPS simulations.
Authors
Jaschke
Wall
Details
The following subroutines / functions are defined for the convergence parameters.
- iMPSOps_f90.TransferMatrixWrapper_mps()[source]¶
fortran-subroutine - ?? () Diagonalize the transfer matrix defined by the unit cell
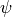 using
the Arnoldi method.
using
the Arnoldi method.Arguments
- psiTYPE(mps), inout
?
- eigvalsREAL(*), inout
?
- VLRTYPE(matrixc), inout
?
- dirCHARACTER, in
‘l’, ‘r’: it indicates the direction
- flagLOGICAL, out
indicate possible symmetry breaking
- errcodeINTEGER, inout
info-flag from DNAUPD, DNEUPD
Source Code
show / hide f90 codesubroutine TransferMatrixWrapper_mps(Psi, eigvals, VLR, dir, flag, & errcode) TYPE(mps) :: psi REAL(KIND=rKind) :: eigVals(:) TYPE(tensorc), POINTER :: VLR(:) CHARACTER, INTENT(IN) :: dir LOGICAL, INTENT(OUT) :: flag INTEGER, INTENT(INOUT) :: errcode ! Logicals to indicate the first loop and calculation of ! eigenvectors in DNEUPD LOGICAL :: rvec, first ! for looping INTEGER :: ii ! number of sites in MPS integer :: qq ! bond dimension to the right of the MPS psi%A(q)%dl(3) integer :: chi ! dimension of the eigenproblem integer :: n ! set zero-parameter DOUBLE PRECISION, PARAMETER :: zero=0.0D+0 ! number of columns in matrix v INTEGER :: ncv ! seems to be an convergence flag (which is set but not used) INTEGER :: nconv ! used for swaping some array INTEGER :: bp ! Counting degenerate eigenvalues INTEGER :: ndeg ! real and complex part of Ritz approximation to eigenvalues DOUBLE PRECISION, ALLOCATABLE :: dr(:), di(:) ! Array for eigenvectors DOUBLE PRECISION, ALLOCATABLE :: v(:,:) ! for sorting the eigenvalues INTEGER, ALLOCATABLE :: indx(:) ! Variables for ARPACK's DNAUPD (described below) ! ----------------------------------------------- integer :: ido, lworkl, nev, ldv character :: bmat*1, which*2 integer :: iparam(11), ipntr(14) DOUBLE PRECISION :: tol DOUBLE PRECISION, ALLOCATABLE :: workl(:), workd(:) DOUBLE PRECISION, ALLOCATABLE :: resid(:) ! Additional for DNEUPD ! --------------------- DOUBLE PRECISION :: sigmar, sigmai DOUBLE PRECISION, ALLOCATABLE :: workev(:) ! internal workspace due to HOWMNY=A (second argument) LOGICAL, ALLOCATABLE :: select_ev(:) ! Intrinsic functions ! -------------------- INTRINSIC :: abs ! General setup ! ============= first = .true. qq = Psi%ll chi = psi%Aa(qq)%dl(3) ! Setup the parameters for DNAUPD ! =============================== ido = 0 ! First call bmat = 'I' ! standard eigenvalue problem A*x = lambda*x n = chi**2 ! Linear size (problem dimension) which = 'LM' ! want the NEV eigenvalues of largest magnitude nev = SIZE(eigvals,1) ! number of eigenvectors desired tol = zero ! some tolerance ldv = n ! leading dimension of the matrix with Arnoldi vectors iparam = (/ 1, 0, 300, 1, 0, 0, 1, 0, 0, 0, 0/) ! [exact shifts, not referenced, max iterations, block size=1, ! number converged Ritz values, not refed, solving A*x = lambda*x, ! shifting if ido=3, total operations, operations B*x, operations re-orth] ! number of columns in matrix V (arnoldi vectors) ncv = MIN(nev * 2 + 50, n) IF(ncv-nev < 2) ncv = nev + 2 ipntr = 0 ! used as pointer-array, intent(out) lworkl = 3*ncv*(ncv+2) ! length of work array workl errcode = 0 ! no initial eigenvector ! and allocate the working arrays ALLOCATE(workl(lworkl), workd(3*n), workev(3*ncv)) ! allocate other stuff ALLOCATE(v(n,ncv), resid(n)) ! Run the diagonalization ! ======================= IF(dir=='l') THEN DO WHILE(ABS(ido)==1.or.first) first=.false. CALL dnaupd ( ido, bmat, n, which, nev, tol, resid, & ncv, v, ldv, iparam, ipntr, workd, workl,& lworkl, errcode ) CALL LeftTransferMatrixMultiply(workd(ipntr(2):ipntr(2)+n-1), psi, & workd(ipntr(1):ipntr(1)+n-1)) END DO ELSE IF(dir=='r') THEN DO WHILE(ABS(ido)==1.or.first) first=.false. CALL dnaupd ( ido, bmat, n, which, nev, tol, resid, & ncv, v, ldv, iparam, ipntr, workd, workl,& lworkl, errcode ) CALL RightTransferMatrixMultiply(workd(ipntr(2):ipntr(2)+n-1),psi,workd(ipntr(1):ipntr(1)+n-1)) END DO END IF IF(errcode.ne.0) THEN write(slog, *) 'nonzero info from dnaupd', errcode DEALLOCATE(v, workl, workd, workev, resid) RETURN ELSE ! Generate eigenvector ALLOCATE(select_ev(ncv), dr(ncv+1), di(ncv+1)) rvec = .true. call dneupd ( rvec, 'A', select_ev, dr,di, v, ldv, sigmar, sigmai, & workev, bmat, n, which, nev, tol, resid, ncv, v, ldv, & iparam, ipntr, workd, workl, lworkl, errcode ) IF ( errcode .ne. 0) then write(slog, *) 'nonzero errcode from dneupd', errcode DEALLOCATE(v, workl,workd, dr,di,workev, resid, select_ev) RETURN ELSE nconv = iparam(5) END IF END IF !Sort eigenvalues in ascending order of magnitude ALLOCATE(indx(SIZE(eigvals,1))) eigvals=ABS(dr(1:SIZE(eigvals))+eye*di(1:SIZE(eigvals))) CALL Descending_hsort(eigvals,indx) !PRINT *, 'raw mag',dr(indx(1:4)),di(indx(1:4)) !PRINT *, 'norms mag',ABS(dr(indx(1:4))+eye*di(indx(1:4))) !Indicate possible symmetry breaking flag=.true. IF(ABS(di(indx(1))).gt.0.1_rKind) THEN flag=.false. END IF !eigvals=dr(1:SIZE(eigvals)) !CALL Descending_hsort(eigvals,indx) !PRINT *, 'raw',dr(indx(1:4)),di(indx(1:4)) !PRINT *, 'norms',ABS(dr(indx(1:4))+eye*di(indx(1:4))) ii = 1 DO WHILE(ii <= SIZE(eigvals,1)-1) IF(di(indx(ii)).ne.zero) THEN IF(di(indx(ii)).gt.zero) THEN !Proper order ensured, move on to the next set ii = ii + 1 ELSE !Swap the order bp=indx(ii) indx(ii)=indx(ii+1) indx(ii+1)=bp ii=ii+1 END IF END IF ii=ii+1 END DO ! Find the degeneracy for the largest eigenvalue ! ---------------------------------------------- ! ! * within a correlation length of 1000 (refers to tolerance 0.0001 ???) eigvals=abs(dr(indx)+eye*di(indx)) ndeg=1 DO ii=2,SIZE(eigvals,1)-1 IF((eigvals(1)-eigvals(ii))/eigvals(1).lt.(10.0_rKind**(-3))) THEN ndeg=ndeg+1 ELSE EXIT END IF END DO ! Generate a set of orthogonal vectors ! ------------------------------------ ! ! * eigenvectors v with eigenvalue (x + iy) and eigenvector u with (x - iy) ! are replaced with: v = v + iu and u = v - iu. These new vector are ! orthogonal (but not normalized anymore if they were before) ALLOCATE(VLR(ndeg)) DO ii=1,ndeg call create(VLR(ii), [chi, chi]) IF(di(indx(ii)).gt.zero) THEN ! PRINT *, 'positive complex',di(indx(i)),di(indx(i+1)) ! PRINT *, 'r and i norms',DOT_PRODUCT(v(:,indx(i)),v(:,indx(i))), DOT_PRODUCT(v(:,indx(i+1)),v(:,indx(i+1))) VLR(ii)%elem = v(:, indx(ii)) + eye * v(:, indx(ii + 1)) ! PRINT *, 'my norm',DOT_PRODUCT(v(:,indx(i))+eye*v(:,indx(i+1)),v(:,indx(i))+eye*v(:,indx(i+1))) ELSE IF(di(indx(ii)).lt.zero) THEN ! PRINT *, 'negative complex',di(indx(i-1)),di(indx(i)) !take v-v^{\star}/(only valid for \epsilon_i\sim 0) ! PRINT *, 'r and i norms',DOT_PRODUCT(v(:,indx(i-1)),v(:,indx(i-1))), DOT_PRODUCT(v(:,indx(i)),v(:,indx(i))) VLR(ii)%elem = v(:, indx(ii - 1)) - eye * v(:, indx(ii)) ! PRINT *, 'my norm',DOT_PRODUCT(v(:,indx(i-1))-eye*v(:,indx(i)),v(:,indx(i-1))-eye*v(:,indx(i))) ELSE VLR(ii)%elem = v(:, indx(ii)) END IF END DO DEALLOCATE(v, workl,workd, dr,di,workev, resid, select_ev,indx) end subroutine TransferMatrixWrapper_mps
- iMPSOps_f90.TransferMatrixWrapper_mpsc()[source]¶
fortran-subroutine - ?? () Diagonalize the transfer matrix defined by the unit cell
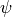 using
the Arnoldi method.
using
the Arnoldi method.Arguments
- psiTYPE(MPSc), inout
?
- eigvalsREAL(*), inout
?
- VLRTYPE(matrixc), inout
?
- dirCHARACTER, in
‘l’, ‘r’: it indicates the direction
- flagLOGICAL, out
indicate possible symmetry breaking
- errcodeINTEGER, inout
info-flag from DNAUPD, DNEUPD
Details
According to M.L. Wall’s thesis and I.P. McCullochs paper Infinite size density matrix renormalization group, revisited (arXiv:0804.2509), the matrix transfer matrix to be diagonalized in this subroutine is always hermitian and non-negative (later) or “hermitian and positive definite when the largest eigenvalue is non-degenerate” (Wall).
Source Code
show / hide f90 codeSUBROUTINE TransferMatrixWrapper_mpsc(psi, eigvals, VLR, dir, flag, & errcode) TYPE(mpsc) :: psi REAL(KIND=rKind) :: eigVals(:) TYPE(tensorc), POINTER :: VLR(:) CHARACTER, INTENT(IN) :: dir LOGICAL, INTENT(OUT) :: flag INTEGER, INTENT(INOUT) :: errcode ! Logicals to indicate 1st loop/calculation of eigenvectors in DNEUPD LOGICAL :: rvec, first ! for looping INTEGER :: ii ! number of sites in MPS integer :: qq ! bond dimension to the right of the MPS psi%A(q)%dl(3) integer :: chi ! dimension of the eigenproblem integer :: n ! set zero-parameter DOUBLE PRECISION, PARAMETER :: zero=0.0D+0 ! number of columns in matrix v INTEGER :: ncv ! seems to be an convergence flag (which is set but not used) INTEGER :: nconv ! used for swaping some array INTEGER :: bp ! Counting degenerate eigenvalues INTEGER :: ndeg ! real and complex part of Ritz approximation to eigenvalues COMPLEX(KIND=rKind), ALLOCATABLE :: dritz(:) ! Array for eigenvectors COMPLEX(KIND=rKind), ALLOCATABLE :: vv(:, :) ! for sorting the eigenvalues INTEGER, ALLOCATABLE :: indx(:) ! Variables for ARPACK's DNAUPD (described below) ! ----------------------------------------------- integer :: ido, lworkl, nev, ldv character :: bmat*1, which*2 integer :: iparam(11), ipntr(14) DOUBLE PRECISION :: tol COMPLEX(KIND=rKind), ALLOCATABLE :: workl(:), workd(:) COMPLEX(KIND=rKind), ALLOCATABLE :: resid(:) DOUBLE PRECISION, ALLOCATABLE :: rwork(:) ! Additional for DNEUPD ! --------------------- COMPLEX(KIND=rKind) :: sigma ! internal workspace due to HOWMNY=A (second argument) LOGICAL, ALLOCATABLE :: select_ev(:) COMPLEX(KIND=rKind), ALLOCATABLE :: workev(:) ! Intrinsic functions ! -------------------- INTRINSIC :: abs ! General setup ! ============= first = .true. qq = Psi%ll chi = Psi%Aa(qq)%dl(3) ! Setup the parameters for DNAUPD ! =============================== ido = 0 ! First call bmat = 'I' ! standard eigenvalue problem A*x = lambda*x n = chi**2 ! Linear size (problem dimension) which = 'LM' ! want the NEV eigenvalues of largest magnitude nev = SIZE(eigvals,1) ! number of eigenvectors desired tol = zero ! some tolerance ldv = n ! leading dimension of the matrix with Arnoldi vectors iparam = (/ 1, 0, 300, 1, 0, 0, 1, 0, 0, 0, 0/) ! [exact shifts, not referenced, max iterations, block size=1, ! number converged Ritz values, not refed, solving A*x = lambda*x, ! shifting if ido=3, total operations, operations B*x, operations re-orth] ipntr = 0 ! used as pointer-array, intent(out) lworkl = 3*ncv*(ncv+2) ! length of work array workl errcode = 0 ! no initial eigenvector ! number of columns in matrix V (arnoldi vectors) ncv = MIN(nev * 2 + 50, n) IF(ncv-nev < 2) ncv = nev + 2 ! and allocate the working arrays ALLOCATE(workl(lworkl), workd(3*n), rwork(ncv)) ! allocate other stuff ALLOCATE(vv(n,ncv), resid(n)) ! Run the diagonalization ! ======================= IF(dir=='l') THEN DO WHILE(ABS(ido)==1.or.first) first=.false. CALL znaupd(ido, bmat, n, which, nev, tol, resid, & ncv, vv, ldv, iparam, ipntr, workd, workl, & lworkl, rwork, errcode) CALL LeftTransferMatrixMultiply(workd(ipntr(2):ipntr(2)+n-1), psi, & workd(ipntr(1):ipntr(1)+n-1)) END DO ELSE IF(dir=='r') THEN DO WHILE(ABS(ido)==1.or.first) first=.false. CALL znaupd(ido, bmat, n, which, nev, tol, resid, & ncv, vv, ldv, iparam, ipntr, workd, workl, & lworkl, rwork, errcode ) CALL RightTransferMatrixMultiply(workd(ipntr(2):ipntr(2)+n-1), psi, & workd(ipntr(1):ipntr(1)+n-1)) END DO END IF IF(errcode.ne.0) THEN write(slog, *) 'nonzero info from dnaupd', errcode DEALLOCATE(vv, workl, workd, resid, rwork) RETURN ELSE ! Generate eigenvector ALLOCATE(select_ev(ncv), dritz(ncv+1), workev(2 * ncv)) rvec = .true. call zneupd(rvec, 'A', select_ev, dritz, vv, ldv, sigma, & workev, bmat, n, which, nev, tol, resid, ncv, vv, ldv, & iparam, ipntr, workd, workl, lworkl, rwork, errcode ) IF(errcode .ne. 0) then write(slog, *) 'nonzero errcode from dneupd', errcode DEALLOCATE(vv, workl, workd, dritz, workev, resid, select_ev, rwork) RETURN ELSE nconv = iparam(5) END IF END IF ! Sort eigenvalues in ascending order of magnitude ALLOCATE(indx(SIZE(eigvals,1))) eigvals = abs(dritz(:size(eigvals))) CALL Descending_hsort(eigvals, indx) ! Indicate possible symmetry breaking flag=.true. if(abs(aimag(dritz(indx(1)))) > 0.1_rKind) then flag = .false. end if ! Sort the eigenvalues such that for pairs of degenerate complex eigenvalues ! (x + i y) is in front of (x - i y) ii = 1 do while(ii <= (size(eigvals, 1) - 1)) if(abs(aimag(dritz(indx(ii)))) > 1.0e-10 .and. & abs(dritz(indx(ii)) - conjg(dritz(indx(ii)))) < 1.0e-10) then ! Found a complex conjugated pair of eigenvalues if(aimag(dritz(indx(ii))) < zero) then ! Swap the order bp=indx(ii) indx(ii)=indx(ii+1) indx(ii+1)=bp ii=ii+1 else ! Good order already installed ii = ii + 1 end if else ! Real eigenvalue - set numerical zero to zero dritz(indx(ii)) = real(dritz(indx(ii))) end if ii = ii + 1 end do write(slog, *) 'swaped eigenvalues' write(slog, *) dritz(indx(1:size(eigvals, 1))) eigvals = abs(dritz(indx)) ! Find all denerate states with the maximal eigenvalue within a corrrelation ! length of 1000 (do not care about degenerated values which are not the ! maximum) ndeg=1 do ii = 2, (size(eigvals, 1) - 1) if((eigvals(1)-eigvals(ii))/eigvals(1) < (10.0_rKind**(-3))) THEN ndeg=ndeg+1 else exit end if end do ! Build a matrix for each degenerate eigenvalue. The eigenvectors ! with chi^2 entries is reshaped into a matrix of size chi x chi ! Build a matrix with all the denerate eigenvalues/-vectors ! For eigenvalues e_j = x + iy and e_k = x - iy and their corresponding ! eigenvectors v_j and v_k the new eigenvectors are defined as the ! following: v_j = v_j + i * v_k and v_k = v_j - i v_k ! (Why do we do this, the norm of the eigenvectors does even change. Are ! they normalised before? Are orthonormal before?) allocate(VLR(ndeg)) do ii = 1, ndeg call create(VLR(ii), [chi, chi]) if(aimag(dritz(indx(ii))) > zero) then ! Complex number in the upper half plane ! TO-DO: NOW V IS ALREADY COMPLEX VLR(ii)%elem = vv(:, indx(ii)) + eye * vv(:, indx(ii + 1)) elseif(aimag(dritz(indx(ii))) < zero) then ! Complex number in the lower half plane ! TO-DO: NOW V IS ALREADY COMPLEX write(slog, *) 'aimag of this truc', & aimag(dritz(indx(ii))), indx(ii) VLR(ii)%elem = vv(:, indx(ii - 1)) - eye * vv(:, indx(ii)) else ! Real eigenvalue VLR(ii)%elem = vv(:, indx(ii)) end if end do DEALLOCATE(vv, workl, workd, dritz, workev, resid, select_ev, indx, rwork) end subroutine TransferMatrixWrapper_mpsc
- iMPSOps_f90.stabilize_tensorc()[source]¶
fortran-subroutine - ?? () Orthonormalize the eigenmatrices Xs and make them Hermitian.
Arguments
- XsTYPE(matrixc)(*), inout
??
Details
This subroutine only exists for complex matrices and has no real counterpart.
Source Code
show / hide f90 codesubroutine stabilize_tensorc(Xs, errst) IMPLICIT NONE TYPE(tensorc), POINTER :: Xs(:) integer, intent(out), optional :: errst ! Local variables ! --------------- INTEGER :: ndeg, i, j, kk TYPE(tensorc), POINTER :: TransXs(:) TYPE(tensorc) :: Overlapmat TYPE(tensor) :: S real(KIND=rKind), dimension(:, :), allocatable :: umat !if(present(errst)) errst = 0 ndeg=SIZE(Xs) call create(Overlapmat, [ndeg, ndeg]) ! Form gram matrix of left eigenvectors kk = 0 do j=1,ndeg do i=1,ndeg kk = kk + 1 Overlapmat%elem(kk) = tracematmul_complex(& Xs(i)%elem, Xs(j)%elem, Xs(i)%dl(1), transl='C') end do end do call create(S, [ndeg]) call eigd_symm_complex(Overlapmat%elem, S%elem, ndeg) write(slog, *) 'eigvals of ev overlap', S%elem !Diagonalize to transform to a basis in which the Gram matrix is the identity ALLOCATE(TransXs(ndeg)) kk = 0 DO i = 1, ndeg call create(Transxs(i), Xs(i)%dl, init='0') do j = 1, ndeg kk = kk + 1 TransXs(i)%elem = TransXs(i)%elem & + overlapmat%elem(kk) * Xs(j)%elem / sqrt(S%elem(i)) end do end do DEALLOCATE(S%elem) ! We now wish to transform to a basis in which all of the matrices ! are Hermitian. Compute the matrix M of hermitian overlaps kk = 0 DO j=1,ndeg DO i=1,ndeg kk = kk + 1 overlapmat%elem(kk) = tracematmul_complex(& Transxs(i)%elem, Transxs(j)%elem, Xs(i)%dl(1), & transl='C', transr='C') end do end do ! Transform the quasi-eigenvalue problem Mc^{\star}=c into an ! eigenvalue problem of twice the size allocate(umat(2 * ndeg, 2 * ndeg)) umat(:ndeg, :ndeg) = & reshape(real(Overlapmat%elem, KIND=rKind), [ndeg, ndeg]) umat(ndeg+1:2*ndeg,ndeg+1:2*ndeg) = & -reshape(real(Overlapmat%elem, KIND=rKind), [ndeg, ndeg]) umat(1:ndeg,ndeg+1:2*ndeg) = & reshape(aimag(Overlapmat%elem), [ndeg, ndeg]) umat(ndeg+1:2*ndeg,1:ndeg) = & reshape(aimag(Overlapmat%elem), [ndeg, ndeg]) call create(S, [2 * ndeg]) call eigd_symm_real(umat, S%elem, 2 * ndeg, errst=errst) !if(prop_error('stabilize_tensorc : eigd failed.', & ! 'iMPSOps_include.f90:691', errst=errst)) return ! Transform to this basis DO i=1,ndeg Xs(i)%elem = 0.0_rKind DO j=1,ndeg Xs(i)%elem = Xs(i)%elem & + (umat(j,ndeg+i) + eye * umat(ndeg+j,ndeg+i))*TRANSXs(j)%elem END DO END DO DO i=1,ndeg CALL Destroy(TransXs(i)) END DO DEALLOCATE(TransXs) deallocate(umat) CALL Destroy(S) CALL Destroy(overlapmat) end subroutine stabilize_tensorc
- iMPSOps_f90.LeftTransferMatrixMultiply_mps()[source]¶
fortran-subroutine - Perform T_{L}(E).
Arguments
- outvecREAL_OR_COMPLEX(*), out
?
- psiTYPE(mps), inout
?
- invecREAL_OR_COMPLEX(*), in
?
Source Code
show / hide f90 codesubroutine LeftTransferMatrixMultiply_mps(outvec, psi, invec, errst) real(KIND=rKind), INTENT(OUT) :: outvec(:) TYPE(mps) :: psi real(KIND=rKind), INTENT(IN) :: invec(:) integer, intent(out), optional :: errst ! Local variables ! --------------- INTEGER :: n,chi,q,i TYPE(tensor) :: Tmp !if(present(errst)) errst = 0 n = SIZE(invec, 1) chi = NINT(sqrt(1.0_rKind*n)) call create(Tmp, [chi, chi]) Tmp%elem = invec q = SIZE(Psi%Aa) DO i=1,q call ptm_right_state(Tmp, Psi%Aa(i), Psi%Aa(i), .false., errst=errst) !if(prop_error('LeftTransferMatrixMultiply_mps: '//& ! 'ptm_right_state failed.', 'iMPSOps_include.f90:780', & ! errst=errst)) return END DO outvec = Tmp%elem call destroy(Tmp) end subroutine LeftTransferMatrixMultiply_mps
- iMPSOps_f90.LeftTransferMatrixMultiply_mpsc()[source]¶
fortran-subroutine - Perform T_{L}(E).
Arguments
- outvecREAL_OR_COMPLEX(*), out
?
- psiTYPE(mpsc), inout
?
- invecREAL_OR_COMPLEX(*), in
?
Source Code
show / hide f90 codesubroutine LeftTransferMatrixMultiply_mpsc(outvec, psi, invec, errst) complex(KIND=rKind), INTENT(OUT) :: outvec(:) TYPE(mpsc) :: psi complex(KIND=rKind), INTENT(IN) :: invec(:) integer, intent(out), optional :: errst ! Local variables ! --------------- INTEGER :: n,chi,q,i TYPE(tensorc) :: Tmp !if(present(errst)) errst = 0 n = SIZE(invec, 1) chi = NINT(sqrt(1.0_rKind*n)) call create(Tmp, [chi, chi]) Tmp%elem = invec q = SIZE(Psi%Aa) DO i=1,q call ptm_right_state(Tmp, Psi%Aa(i), Psi%Aa(i), .false., errst=errst) !if(prop_error('LeftTransferMatrixMultiply_mpsc: '//& ! 'ptm_right_state failed.', 'iMPSOps_include.f90:780', & ! errst=errst)) return END DO outvec = Tmp%elem call destroy(Tmp) end subroutine LeftTransferMatrixMultiply_mpsc
- iMPSOps_f90.GetLambdaR_tensor()[source]¶
fortran-subroutine - ?? () Given the tensor A of the unit cell in o.c. form, extract
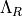 .
.Arguments
- ATYPE(tensor), inout
the tensor for the orthogonality center
- LambdaRTYPE(tensor), out
A dense matrix
 were
were 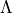 is
matrix containing the singular values and V the right unitary matrix
from the SVD of
is
matrix containing the singular values and V the right unitary matrix
from the SVD of 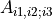 (i1, i2 build the rows of matrix)
(i1, i2 build the rows of matrix)
Source Code
show / hide f90 codesubroutine GetLambdaR_tensor(A, LambdaR) type(tensor), intent(inout) :: A type(tensor), intent(out) :: LambdaR ! Local variables ! --------------- ! left and right unitary matrices of SVD TYPE(tensor) :: Ut, Vt ! vector with singular values TYPE(tensor) :: Lam call svd(Ut, Lam, LambdaR, A, [1, 2], [3], multlr=1) call destroy(Ut) call destroy(Lam) end subroutine GetLambdaR_tensor
- iMPSOps_f90.GetLambdaR_tensorc()[source]¶
fortran-subroutine - ?? () Given the tensor A of the unit cell in o.c. form, extract
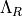 .
.Arguments
- ATYPE(tensorc), inout
the tensor for the orthogonality center
- LambdaRTYPE(tensorc), out
A dense matrix
 were
were 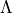 is
matrix containing the singular values and V the right unitary matrix
from the SVD of
is
matrix containing the singular values and V the right unitary matrix
from the SVD of 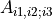 (i1, i2 build the rows of matrix)
(i1, i2 build the rows of matrix)
Source Code
show / hide f90 codesubroutine GetLambdaR_tensorc(A, LambdaR) type(tensorc), intent(inout) :: A type(tensorc), intent(out) :: LambdaR ! Local variables ! --------------- ! left and right unitary matrices of SVD TYPE(tensorc) :: Ut, Vt ! vector with singular values TYPE(tensor) :: Lam call svd(Ut, Lam, LambdaR, A, [1, 2], [3], multlr=1) call destroy(Ut) call destroy(Lam) end subroutine GetLambdaR_tensorc
- iMPSOps_f90.GetLongLambdaR_mps()[source]¶
fortran-subroutine - ?? () Extract
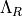 , defined as the right boundary term on a
completely (!) gauged MPS, so orthogonality center at
, defined as the right boundary term on a
completely (!) gauged MPS, so orthogonality center at 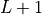 .
.Arguments
- psiTYPE(mps), in
Get some singular values of this MPS
- LambdaRTYPE(tensor), out
dense matrix of singular values times a unitary matrix as left over from installing a unitary matrix on the last site.
Source Code
show / hide f90 codesubroutine GetLongLambdaR_mps(Psi, LambdaR) type(mps), intent(in) :: Psi type(tensor), intent(out) :: LambdaR ! Local variables ! --------------- ! temporary copy of psi / psi is not modified that way type(mps) :: Psit call copy(Psit, Psi) call canonize_svd(Psit, Psit%ll, Psit%oc, Psit%ll) call GetLambdaR(Psit%Aa(Psit%ll), LambdaR) call destroy(Psit) end subroutine GetLongLambdaR_mps
- iMPSOps_f90.GetLongLambdaR_mpsc()[source]¶
fortran-subroutine - ?? () Extract
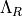 , defined as the right boundary term on a
completely (!) gauged MPS, so orthogonality center at
, defined as the right boundary term on a
completely (!) gauged MPS, so orthogonality center at 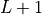 .
.Arguments
- psiTYPE(mpsc), in
Get some singular values of this MPS
- LambdaRTYPE(tensorc), out
dense matrix of singular values times a unitary matrix as left over from installing a unitary matrix on the last site.
Source Code
show / hide f90 codesubroutine GetLongLambdaR_mpsc(Psi, LambdaR) type(mpsc), intent(in) :: Psi type(tensorc), intent(out) :: LambdaR ! Local variables ! --------------- ! temporary copy of psi / psi is not modified that way type(mpsc) :: Psit call copy(Psit, Psi) call canonize_svd(Psit, Psit%ll, Psit%oc, Psit%ll) call GetLambdaR(Psit%Aa(Psit%ll), LambdaR) call destroy(Psit) end subroutine GetLongLambdaR_mpsc
- iMPSOps_f90.OrthogonalityFidelity_mps()[source]¶
fortran-subroutine - ?? () Calculate the orthogonality fidelity :math:``
Arguments
- psiTYPE(mps), in
Use psi to calculate orthogonality fidelity to lastlam.
- ofREAL, out
on exit the orthogonality fidelity
- lastlamTYPE(tensor), in
dense matrix with singular values on the diagonal???
Source Code
show / hide f90 codesubroutine OrthogonalityFidelity_mps(Psi, of, Lastlam) TYPE(mps), intent(in) :: Psi REAL(KIND=rKind), intent(out) :: of TYPE(tensor), intent(inout) :: Lastlam ! Local variables ! --------------- ! containing singular values of the SVD TYPE(tensor) :: S ! unitary matrices from SVD TYPE(tensor) :: U, V TYPE(tensor) :: LambdaR, OFMat ! Check orthogonality fidelity call GetLongLambdaR(Psi, LambdaR) call contr(Ofmat, LambdaR, Lastlam, [2], [1]) call destroy(LambdaR) call svd(U, S, V, OFmat, [1], [2]) call destroy(U) call destroy(OFmat) call destroy(V) of = sum(S%elem) call destroy(S) end subroutine OrthogonalityFidelity_mps
- iMPSOps_f90.OrthogonalityFidelity_mpsc()[source]¶
fortran-subroutine - ?? () Calculate the orthogonality fidelity :math:``
Arguments
- psiTYPE(mpsc), in
Use psi to calculate orthogonality fidelity to lastlam.
- ofREAL, out
on exit the orthogonality fidelity
- lastlamTYPE(tensorc), in
dense matrix with singular values on the diagonal???
Source Code
show / hide f90 codesubroutine OrthogonalityFidelity_mpsc(Psi, of, Lastlam) TYPE(mpsc), intent(in) :: Psi REAL(KIND=rKind), intent(out) :: of TYPE(tensorc), intent(inout) :: Lastlam ! Local variables ! --------------- ! containing singular values of the SVD TYPE(tensor) :: S ! unitary matrices from SVD TYPE(tensorc) :: U, V TYPE(tensorc) :: LambdaR, OFMat ! Check orthogonality fidelity call GetLongLambdaR(Psi, LambdaR) call contr(Ofmat, LambdaR, Lastlam, [2], [1]) call destroy(LambdaR) call svd(U, S, V, OFmat, [1], [2]) call destroy(U) call destroy(OFmat) call destroy(V) of = sum(S%elem) call destroy(S) end subroutine OrthogonalityFidelity_mpsc
- iMPSOps_f90.LongPredict_mps()[source]¶
fortran-subroutine - ?? ()
Arguments
- psiTYPE(mps), inout
??
- LambdaTYPE(MATRIX_TYPE), inout
??
- Lambdanm1TYPE(MATRIX_TYPE), inout
?? on exit destroyed
Details
The SVD on a diagonal matrix is a remaining part from a version where the Lambdanm1 matrix was not diagonal.
Source Code
show / hide f90 codesubroutine LongPredict_mps(Psi, Lambda, Lambdanm1, errst) type(mps), intent(inout) :: Psi type(tensor), intent(inout) :: Lambda integer, intent(out), optional :: errst ! originally intent(in), but used as workspace type(tensor), intent(inout) :: Lambdanm1 ! Local variables ! --------------- ! for looping integer :: ii integer :: newoc, nleftsites integer :: alp, beta, oldoc real(KIND=rKind) :: tol, zip, mynorm type(mps) :: psit type(tensor) :: Atmp, Btmp type(tensor) :: Sing type(tensor) :: Um, Vm !if(present(errst)) errst = 0 ! Save oc oldoc = Psi%oc ! use McCulloch's prediction to get a new guess at the unit cell !Copy MPS call copy(Psit, Psi) call destroy(Psit%Aa(oldoc + 1)) ! (Lambda B) BBBBBBBBBBBBBB call contr(Psit%Aa(oldoc + 1), Lambda, Psi%Aa(oldoc + 1), [2], [1], & errst=errst) !if(prop_error('LongPredict_mps: contr failed.', & ! 'iMPSOps_include.f90:1268', errst=errst)) return Psit%oc = oldoc + 1 ! Move oc all the way to the right !BBBBBBBBBBB(Lambda B) call canonize_svd(Psit, Psit%ll, oldoc + 1, Psit%ll) ! AAAAAAAAAAAA (A Lambda) call destroy(Psit%Aa(oldoc)) call contr(Psit%Aa(oldoc), Psi%Aa(oldoc), Lambda, [3], [1], & errst=errst) !if(prop_error('LongPredict_mps: contr failed.', & ! 'iMPSOps_include.f90:1281', errst=errst)) return !Move oc all the way to the left ! (A Lambda) AAAAAAA call canonize_svd(Psit, 1, 1, oldoc) ! pseudoinvert Lambda_{n-1} call svd(Um, Sing, Vm, Lambdanm1, [1], [2], errst=errst) !if(prop_error('LongPredict_mps: svd failed.', & ! 'iMPSOps_include.f90:1290', errst=errst)) return tol = Sing%dl(1) * maxvalue(Sing) * numzero do ii = 1, Sing%dl(1) if(Sing%elem(ii) > tol) then Sing%elem(ii) = 1.0_rKind / Sing%elem(ii) else Sing%elem(ii) = 0.0_rKind end if end do call contr_diag(Um, Sing, 2, errst=errst) !if(prop_error('LongPredict_mps: contr_diag failed.', & ! 'iMPSOps_include.f90:1303', errst=errst)) return call destroy(Lambdanm1) call contr(Lambdanm1, Vm, Um, [2], [1], errst=errst) !if(prop_error('LongPredict_mps: contr failed.', & ! 'iMPSOps_include.f90:1308', errst=errst)) return call destroy(Um) call destroy(Vm) call destroy(Sing) ! Lambda_{n-1}^{-1} (A Lambda) AAAAAAAAAA call contr(Atmp, Lambdanm1, Psit%Aa(1), [2], [1], errst=errst) !if(prop_error('LongPredict_mps: contr failed.', & ! 'iMPSOps_include.f90:1317', errst=errst)) return call destroy(Psit%Aa(1)) call pointto(Psit%Aa(1), Atmp) call destroy(Lambdanm1) call destroy(Psi) Psi%ll = Psit%ll allocate(Psi%AA(Psit%ll), Psi%can(Psi%ll), Psi%Lambda(Psi%ll + 1), & Psi%haslambda(Psi%ll + 1)) Psi%haslambda = .false. Psi%can = 'o' do ii = 1, (Psit%ll - oldoc) call copy(Psi%Aa(ii), Psit%Aa(oldoc + ii)) end do do ii = 1, oldoc call copy(Psi%Aa(Psi%ll - oldoc + ii), Psit%Aa(ii)) end do Psi%oc = -1 call destroy(Psit) call canonize_svd(Psi, Psi%ll, 1, Psi%ll) call canonize_svd(Psi, 1, 1, Psi%ll) call canonize_svd(Psi, Psi%ll - oldoc, 1, Psi%ll) mynorm = norm(Psi) call scale(1.0_rKind / sqrt(mynorm), Psi) end subroutine LongPredict_mps
- iMPSOps_f90.LongPredict_mpsc()[source]¶
fortran-subroutine - ?? ()
Arguments
- psiTYPE(mpsc), inout
??
- LambdaTYPE(MATRIX_TYPE), inout
??
- Lambdanm1TYPE(MATRIX_TYPE), inout
?? on exit destroyed
Details
The SVD on a diagonal matrix is a remaining part from a version where the Lambdanm1 matrix was not diagonal.
Source Code
show / hide f90 codesubroutine LongPredict_mpsc(Psi, Lambda, Lambdanm1, errst) type(mpsc), intent(inout) :: Psi type(tensorc), intent(inout) :: Lambda integer, intent(out), optional :: errst ! originally intent(in), but used as workspace type(tensorc), intent(inout) :: Lambdanm1 ! Local variables ! --------------- ! for looping integer :: ii integer :: newoc, nleftsites integer :: alp, beta, oldoc real(KIND=rKind) :: tol, zip, mynorm type(mpsc) :: psit type(tensorc) :: Atmp, Btmp type(tensor) :: Sing type(tensorc) :: Um, Vm !if(present(errst)) errst = 0 ! Save oc oldoc = Psi%oc ! use McCulloch's prediction to get a new guess at the unit cell !Copy MPS call copy(Psit, Psi) call destroy(Psit%Aa(oldoc + 1)) ! (Lambda B) BBBBBBBBBBBBBB call contr(Psit%Aa(oldoc + 1), Lambda, Psi%Aa(oldoc + 1), [2], [1], & errst=errst) !if(prop_error('LongPredict_mpsc: contr failed.', & ! 'iMPSOps_include.f90:1268', errst=errst)) return Psit%oc = oldoc + 1 ! Move oc all the way to the right !BBBBBBBBBBB(Lambda B) call canonize_svd(Psit, Psit%ll, oldoc + 1, Psit%ll) ! AAAAAAAAAAAA (A Lambda) call destroy(Psit%Aa(oldoc)) call contr(Psit%Aa(oldoc), Psi%Aa(oldoc), Lambda, [3], [1], & errst=errst) !if(prop_error('LongPredict_mpsc: contr failed.', & ! 'iMPSOps_include.f90:1281', errst=errst)) return !Move oc all the way to the left ! (A Lambda) AAAAAAA call canonize_svd(Psit, 1, 1, oldoc) ! pseudoinvert Lambda_{n-1} call svd(Um, Sing, Vm, Lambdanm1, [1], [2], errst=errst) !if(prop_error('LongPredict_mpsc: svd failed.', & ! 'iMPSOps_include.f90:1290', errst=errst)) return tol = Sing%dl(1) * maxvalue(Sing) * numzero do ii = 1, Sing%dl(1) if(Sing%elem(ii) > tol) then Sing%elem(ii) = 1.0_rKind / Sing%elem(ii) else Sing%elem(ii) = 0.0_rKind end if end do call contr_diag(Um, Sing, 2, errst=errst) !if(prop_error('LongPredict_mpsc: contr_diag failed.', & ! 'iMPSOps_include.f90:1303', errst=errst)) return call destroy(Lambdanm1) call contr(Lambdanm1, Vm, Um, [2], [1], errst=errst) !if(prop_error('LongPredict_mpsc: contr failed.', & ! 'iMPSOps_include.f90:1308', errst=errst)) return call destroy(Um) call destroy(Vm) call destroy(Sing) ! Lambda_{n-1}^{-1} (A Lambda) AAAAAAAAAA call contr(Atmp, Lambdanm1, Psit%Aa(1), [2], [1], errst=errst) !if(prop_error('LongPredict_mpsc: contr failed.', & ! 'iMPSOps_include.f90:1317', errst=errst)) return call destroy(Psit%Aa(1)) call pointto(Psit%Aa(1), Atmp) call destroy(Lambdanm1) call destroy(Psi) Psi%ll = Psit%ll allocate(Psi%AA(Psit%ll), Psi%can(Psi%ll), Psi%Lambda(Psi%ll + 1), & Psi%haslambda(Psi%ll + 1)) Psi%haslambda = .false. Psi%can = 'o' do ii = 1, (Psit%ll - oldoc) call copy(Psi%Aa(ii), Psit%Aa(oldoc + ii)) end do do ii = 1, oldoc call copy(Psi%Aa(Psi%ll - oldoc + ii), Psit%Aa(ii)) end do Psi%oc = -1 call destroy(Psit) call canonize_svd(Psi, Psi%ll, 1, Psi%ll) call canonize_svd(Psi, 1, 1, Psi%ll) call canonize_svd(Psi, Psi%ll - oldoc, 1, Psi%ll) mynorm = norm(Psi) call scale(1.0_rKind / sqrt(mynorm), Psi) end subroutine LongPredict_mpsc
- iMPSOps_f90.prepare_mps()[source]¶
fortran-subroutine - ???
Arguments
- nextlamTYPE(matrix), inout
filled/overwritten during subroutine. Is a dense matrix containing some Schmidt values of the MPS on the diagonal.
- lastlamTYPE(matrix), inout
overwritten during subroutine. Is a dense matrix containing some Schmidt values of the MPS on the diagonal.
Source Code
show / hide f90 codesubroutine prepare_mps(Psi, LR, LLLE, LRE, H, energy, Nextlam, Lastlam, & numleft, fl, maxbondd, errst) type(mps) :: Psi type(tensorlist), dimension(:), allocatable, intent(inout) :: LR type(tensorlist) :: LLLE, LRE type(mpo) :: H real(KIND=rKind) :: energy type(tensor), intent(inout) :: Nextlam, Lastlam integer :: numleft, maxbondd logical :: fl integer, intent(out), optional :: errst ! for looping integer :: ii ! shortcut for length of the MPS integer :: qq ! ??? (only reference once) real(KIND=rKind) :: zip ! Two-site tensor type(tensor) :: Theta !if(present(errst)) errst = 0 qq = Psi%ll numleft = floor(0.5_rKind * qq) !Extract o.c. and form new environment call copy(Nextlam, Lastlam) call destroy(Lastlam) fl = .true. call canonize_svd(Psi, numleft, 1, Psi%ll, errst=errst) !if(prop_error('prepare_mps : canonize_svd failed.', & ! 'iMPSOps_include.f90:1427', errst=errst)) return !if(.not. Psi%haslambda(Psi%oc + 1)) then ! errst = raise_error('prepare_mps: Lambda not set.', & ! 99, 'iMPSOps_include.f90:1431', errst=errst) ! return !end if call contr(Theta, Psi%Aa(Psi%oc), Psi%Aa(Psi%oc + 1), [3], [1], & errst=errst) !if(prop_error('prepare_mps : contr failed.', & ! 'iMPSOps_include.f90:1438', errst=errst)) return call destroy(Psi%Aa(Psi%oc)) call destroy(Psi%Aa(Psi%oc + 1)) if(Psi%haslambda(Psi%oc + 1)) call destroy(Psi%Lambda(Psi%oc + 1)) ! To-Do: set chi call svd(Psi%Aa(Psi%oc), Psi%Lambda(Psi%oc + 1), Psi%Aa(Psi%oc + 1), & Theta, [1, 2], [3, 4], errst=errst) !if(prop_error('prepare_mps : svd failed.', & ! 'iMPSOps_include.f90:1448', errst=errst)) return call destroy(Theta) call create_diag(Lastlam, Psi%Lambda(Psi%oc + 1), errst=errst) !if(prop_error('prepare_mps : create_diag failed.', & ! 'iMPSOps_include.f90:1454', errst=errst)) return call shift(H%Wb, energy / (qq * 1.0_rKind), errst=errst) !if(prop_error('prepare_mps : shift failed.', & ! 'iMPSOps_include.f90:1458', errst=errst)) return allocate(LR(Psi%ll + 1)) ! Set up LR(1) call ptm_right_mpo(LR(1), Psi%Aa(1), H%Wb, Psi%Aa(1), .false., & Matin=LLLE, errst=errst) !if(prop_error('prepare_mps : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1466', errst=errst)) return call destroy(LLLE) do ii = 2, Psi%oc call ptm_right_mpo(LLLE, Psi%Aa(ii), H%Wb, Psi%Aa(ii), .false., & Matin=LR(1), errst=errst) !if(prop_error('prepare_mps : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1474', errst=errst)) return call destroy(LR(1)) call copy(LR(1), LLLE) call destroy(LLLE) end do call ptm_left_mpo(LR(Psi%ll + 1), Psi%Aa(Psi%ll), H%Wb, Psi%Aa(Psi%ll), & .false., Matin=LRE, errst=errst) !if(prop_error('prepare_mps : ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1484', errst=errst)) return call destroy(LRE) do ii = (Psi%ll - 1), (Psi%oc + 1), (-1) call ptm_left_mpo(LRE, Psi%Aa(ii), H%Wb, Psi%Aa(ii), & .false., Matin=LR(Psi%ll + 1), errst=errst) !if(prop_error('prepare_mps : ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1492', errst=errst)) return call destroy(LR(Psi%ll + 1)) call copy(LR(Psi%ll + 1), LRE) call destroy(LRE) end do ! LR(1) and LR(L+1) are now the new boundary environments ! save them for future use call copy(LLLE, LR(1)) call copy(LRE, LR(Psi%ll + 1)) ! Shift MPOs back call shift(H%Wb, -energy / (qq * 1.0_rKind), errst=errst) !if(prop_error('prepare_mps : shift failed.', & ! 'iMPSOps_include.f90:1507', errst=errst)) return ! Predict call LongPredict(Psi, Lastlam, Nextlam, errst=errst) !if(prop_error('prepare_mps : LongPredict failed.', & ! 'iMPSOps_include.f90:1512', errst=errst)) return ! setup LR do ii = Psi%ll, (Psi%oc + 1), (-1) call ptm_left_mpo(LR(ii), Psi%Aa(ii), H%Wb, Psi%Aa(ii), & .false., Matin=LR(ii + 1), errst=errst) !if(prop_error('prepare_mps : ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1519', errst=errst)) return end do do ii = 2, Psi%oc call ptm_right_mpo(LR(ii), Psi%Aa(ii - 1), H%Wb, Psi%Aa(ii - 1), & .false., Matin=LR(ii - 1), errst=errst) !if(prop_error('prepare_mps : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1526', errst=errst)) return end do end subroutine prepare_mps
- iMPSOps_f90.prepare_mpsc()[source]¶
fortran-subroutine - ???
Arguments
- nextlamTYPE(matrix), inout
filled/overwritten during subroutine. Is a dense matrix containing some Schmidt values of the MPS on the diagonal.
- lastlamTYPE(matrix), inout
overwritten during subroutine. Is a dense matrix containing some Schmidt values of the MPS on the diagonal.
Source Code
show / hide f90 codesubroutine prepare_mpsc(Psi, LR, LLLE, LRE, H, energy, Nextlam, Lastlam, & numleft, fl, maxbondd, errst) type(mpsc) :: Psi type(tensorlistc), dimension(:), allocatable, intent(inout) :: LR type(tensorlistc) :: LLLE, LRE type(mpoc) :: H real(KIND=rKind) :: energy type(tensorc), intent(inout) :: Nextlam, Lastlam integer :: numleft, maxbondd logical :: fl integer, intent(out), optional :: errst ! for looping integer :: ii ! shortcut for length of the MPS integer :: qq ! ??? (only reference once) real(KIND=rKind) :: zip ! Two-site tensor type(tensorc) :: Theta !if(present(errst)) errst = 0 qq = Psi%ll numleft = floor(0.5_rKind * qq) !Extract o.c. and form new environment call copy(Nextlam, Lastlam) call destroy(Lastlam) fl = .true. call canonize_svd(Psi, numleft, 1, Psi%ll, errst=errst) !if(prop_error('prepare_mpsc : canonize_svd failed.', & ! 'iMPSOps_include.f90:1427', errst=errst)) return !if(.not. Psi%haslambda(Psi%oc + 1)) then ! errst = raise_error('prepare_mpsc: Lambda not set.', & ! 99, 'iMPSOps_include.f90:1431', errst=errst) ! return !end if call contr(Theta, Psi%Aa(Psi%oc), Psi%Aa(Psi%oc + 1), [3], [1], & errst=errst) !if(prop_error('prepare_mpsc : contr failed.', & ! 'iMPSOps_include.f90:1438', errst=errst)) return call destroy(Psi%Aa(Psi%oc)) call destroy(Psi%Aa(Psi%oc + 1)) if(Psi%haslambda(Psi%oc + 1)) call destroy(Psi%Lambda(Psi%oc + 1)) ! To-Do: set chi call svd(Psi%Aa(Psi%oc), Psi%Lambda(Psi%oc + 1), Psi%Aa(Psi%oc + 1), & Theta, [1, 2], [3, 4], errst=errst) !if(prop_error('prepare_mpsc : svd failed.', & ! 'iMPSOps_include.f90:1448', errst=errst)) return call destroy(Theta) call create_diag(Lastlam, Psi%Lambda(Psi%oc + 1), errst=errst) !if(prop_error('prepare_mpsc : create_diag failed.', & ! 'iMPSOps_include.f90:1454', errst=errst)) return call shift(H%Wb, energy / (qq * 1.0_rKind), errst=errst) !if(prop_error('prepare_mpsc : shift failed.', & ! 'iMPSOps_include.f90:1458', errst=errst)) return allocate(LR(Psi%ll + 1)) ! Set up LR(1) call ptm_right_mpo(LR(1), Psi%Aa(1), H%Wb, Psi%Aa(1), .false., & Matin=LLLE, errst=errst) !if(prop_error('prepare_mpsc : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1466', errst=errst)) return call destroy(LLLE) do ii = 2, Psi%oc call ptm_right_mpo(LLLE, Psi%Aa(ii), H%Wb, Psi%Aa(ii), .false., & Matin=LR(1), errst=errst) !if(prop_error('prepare_mpsc : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1474', errst=errst)) return call destroy(LR(1)) call copy(LR(1), LLLE) call destroy(LLLE) end do call ptm_left_mpo(LR(Psi%ll + 1), Psi%Aa(Psi%ll), H%Wb, Psi%Aa(Psi%ll), & .false., Matin=LRE, errst=errst) !if(prop_error('prepare_mpsc : ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1484', errst=errst)) return call destroy(LRE) do ii = (Psi%ll - 1), (Psi%oc + 1), (-1) call ptm_left_mpo(LRE, Psi%Aa(ii), H%Wb, Psi%Aa(ii), & .false., Matin=LR(Psi%ll + 1), errst=errst) !if(prop_error('prepare_mpsc : ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1492', errst=errst)) return call destroy(LR(Psi%ll + 1)) call copy(LR(Psi%ll + 1), LRE) call destroy(LRE) end do ! LR(1) and LR(L+1) are now the new boundary environments ! save them for future use call copy(LLLE, LR(1)) call copy(LRE, LR(Psi%ll + 1)) ! Shift MPOs back call shift(H%Wb, -energy / (qq * 1.0_rKind), errst=errst) !if(prop_error('prepare_mpsc : shift failed.', & ! 'iMPSOps_include.f90:1507', errst=errst)) return ! Predict call LongPredict(Psi, Lastlam, Nextlam, errst=errst) !if(prop_error('prepare_mpsc : LongPredict failed.', & ! 'iMPSOps_include.f90:1512', errst=errst)) return ! setup LR do ii = Psi%ll, (Psi%oc + 1), (-1) call ptm_left_mpo(LR(ii), Psi%Aa(ii), H%Wb, Psi%Aa(ii), & .false., Matin=LR(ii + 1), errst=errst) !if(prop_error('prepare_mpsc : ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1519', errst=errst)) return end do do ii = 2, Psi%oc call ptm_right_mpo(LR(ii), Psi%Aa(ii - 1), H%Wb, Psi%Aa(ii - 1), & .false., Matin=LR(ii - 1), errst=errst) !if(prop_error('prepare_mpsc : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1526', errst=errst)) return end do end subroutine prepare_mpsc
- iMPSOps_f90.leftorthogonalize_mps()[source]¶
fortran-subroutine - ?? () Form the left-orthogonalized unit cell
Arguments
- psiTYPE(mps), in
MPS to be orthogonalized
psit : TYPE(mps)(*), out
- XsTYPE(tensor)(*), in
???
- YsTYPE(tensor)(*), in
???
- lambdaRinvsTYPE(tensor)(*), in
???
Details
The array of left orthogonalized unit cells for each degenerate eigenvalue is built (degenerate eigenvalue of the transfer matrix). Each MPS is modified in the following way:
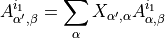
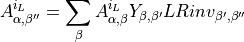
The resulting MPS is canonized via SVDs.
Source Code
show / hide f90 codesubroutine leftorthogonalize_mps(Psi, Psit, Xs, Ys, LambdaRinvs, errst) type(mps), intent(in) :: Psi type(mps), intent(out), pointer :: psit(:) type(tensor), intent(in), pointer :: Xs(:), Ys(:), lambdaRinvs(:) integer, intent(out), optional :: errst ! Local variables ! --------------- ! for looping integer :: jj ! for number of sites of MPS integer :: qq ! temporary tensor for contraction TYPE(tensor) :: Atmp !if(present(errst)) errst = 0 qq = Psi%ll allocate(Psit(size(Xs, 1))) do jj = 1, size(Psit, 1) ! Form properly left-orthogonalized unit cell for expectation values call copy(Psit(jj), Psi) ! Absorb X into A^1 CALL contr(Atmp, Xs(jj), Psit(jj)%Aa(1), [2], [1], errst=errst) !if(prop_error('leftorthogonalize_mps', & ! 'iMPSOps_include.f90:1699', errst=errst)) return call destroy(Psit(jj)%Aa(1)) call copy(Psit(jj)%Aa(1), Atmp) call destroy(Atmp) ! Construct B^q(new) = B^q - Y - LambdaRinvs = tmp - LambdaRinvs call contr(Atmp, Psit(jj)%Aa(qq), Ys(jj), [3], [1], errst=errst) !if(prop_error('leftorthogonalize_mps', & ! 'iMPSOps_include.f90:1708', errst=errst)) return call destroy(Psit(jj)%Aa(qq)) ! Combine ilde{\Lambda_{n-1}} to define TI unit cell of left-orthog. matrices call contr(Psit(jj)%Aa(qq), Atmp, LambdaRinvs(jj), [3], [1], & errst=errst) !if(prop_error('leftorthogonalize_mps', & ! 'iMPSOps_include.f90:1716', errst=errst)) return call destroy(Atmp) ! Bring into canonical form call canonize_svd(Psit(jj), 1, 1, Psit(jj)%ll) call canonize_svd(Psit(jj), Psit(jj)%ll, 1, Psit(jj)%ll) Psit(jj)%can = 'l' end do end subroutine leftorthogonalize_mps
- iMPSOps_f90.leftorthogonalize_mpsc()[source]¶
fortran-subroutine - ?? () Form the left-orthogonalized unit cell
Arguments
- psiTYPE(mpsc), in
MPS to be orthogonalized
psit : TYPE(mpsc)(*), out
- XsTYPE(tensorc)(*), in
???
- YsTYPE(tensorc)(*), in
???
- lambdaRinvsTYPE(tensorc)(*), in
???
Details
The array of left orthogonalized unit cells for each degenerate eigenvalue is built (degenerate eigenvalue of the transfer matrix). Each MPS is modified in the following way:
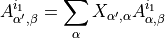
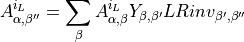
The resulting MPS is canonized via SVDs.
Source Code
show / hide f90 codesubroutine leftorthogonalize_mpsc(Psi, Psit, Xs, Ys, LambdaRinvs, errst) type(mpsc), intent(in) :: Psi type(mpsc), intent(out), pointer :: psit(:) type(tensorc), intent(in), pointer :: Xs(:), Ys(:), lambdaRinvs(:) integer, intent(out), optional :: errst ! Local variables ! --------------- ! for looping integer :: jj ! for number of sites of MPS integer :: qq ! temporary tensor for contraction TYPE(tensorc) :: Atmp !if(present(errst)) errst = 0 qq = Psi%ll allocate(Psit(size(Xs, 1))) do jj = 1, size(Psit, 1) ! Form properly left-orthogonalized unit cell for expectation values call copy(Psit(jj), Psi) ! Absorb X into A^1 CALL contr(Atmp, Xs(jj), Psit(jj)%Aa(1), [2], [1], errst=errst) !if(prop_error('leftorthogonalize_mpsc', & ! 'iMPSOps_include.f90:1699', errst=errst)) return call destroy(Psit(jj)%Aa(1)) call copy(Psit(jj)%Aa(1), Atmp) call destroy(Atmp) ! Construct B^q(new) = B^q - Y - LambdaRinvs = tmp - LambdaRinvs call contr(Atmp, Psit(jj)%Aa(qq), Ys(jj), [3], [1], errst=errst) !if(prop_error('leftorthogonalize_mpsc', & ! 'iMPSOps_include.f90:1708', errst=errst)) return call destroy(Psit(jj)%Aa(qq)) ! Combine ilde{\Lambda_{n-1}} to define TI unit cell of left-orthog. matrices call contr(Psit(jj)%Aa(qq), Atmp, LambdaRinvs(jj), [3], [1], & errst=errst) !if(prop_error('leftorthogonalize_mpsc', & ! 'iMPSOps_include.f90:1716', errst=errst)) return call destroy(Atmp) ! Bring into canonical form call canonize_svd(Psit(jj), 1, 1, Psit(jj)%ll) call canonize_svd(Psit(jj), Psit(jj)%ll, 1, Psit(jj)%ll) Psit(jj)%can = 'l' end do end subroutine leftorthogonalize_mpsc
- iMPSOps_f90.InfiniteMPS_mps()[source]¶
fortran-subroutine - ?? () Use the infinite size algorithm to find the fixed point in the infinite size limit.
Arguments
- HTYPE(MPO), inout
containing the Hamiltonian of the system.
- qINTEGER, inout
Most probably the length of the unit cell
- OperatorsTYPE(matrixList), inout
List of all the operators used in the Hamiltonian and measurements
- MyObsTYPE(obs_r), inout
Settings with the observables to be measured
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
The infinite MPS algorithm is described in I.P. McCulloch’s paper “Infinite size density renormalization group, revisited”, arXiv0804.2509
Source Code
show / hide f90 codesubroutine InfiniteMPS_mps(Ham, q, Operators, MyObs, & IOObj, Imapper, pbc, errst) use ioops, only : cpunit, obsunit type(mpo), intent(inout) :: Ham integer, intent(in) :: q type(tensorlist) :: Operators type(obs_r) :: MyObs type(IOObject), intent(in) :: IOObj type(imap), intent(in) :: Imapper logical, intent(in) :: pbc integer, intent(out), optional :: errst ! Local variables ! --------------- ! for looping integer :: ii ! local convergence parameter warmup chi integer :: warmup_bond_dimension ! arrays for quantum numbers integer, dimension(2) :: nqs integer, dimension(0) :: qs ! local convergence parameter variance tol / warmup_tol real(KIND=rKind) :: variance_tol, warmup_tol ! Filename for measurement character(len=132) :: obsname REAL(KIND=rKind) :: gmrestol TYPE(mps) :: psi TYPE(mps), POINTER :: psic(:) TYPE(tensorlist) :: LLLE, LRE TYPE(tensorlist), dimension(:), allocatable :: LR ! In the basis we work this contains only real values on the diagonal. ! If you choose to work in another basis, this would be a dense matrix. ! Using complex one is as well the most general case. Allover there is ! some overhead here. TYPE(tensor) :: lastlam ! Since nextlam is a copy of lastlam, the same arguments apply here TYPE(tensor) :: nextlam TYPE(tensor), POINTER :: XS(:), Ys(:), lambdaRs(:), lambdaRinvs(:) REAL(KIND=rKind) :: zip, energy, err, of, oftol, variance, vtsave INTEGER :: nchis, whichchi INTEGER :: i INTEGER :: ninner, errcode LOGICAL :: ifail, conver,converged, fl INTEGER :: nbelow, numleft, ndeg ! Two-site tensor type(tensor) :: Theta ! convergence parameters type(ConvParam), dimension(:), allocatable :: Cps ! All two-site MPO matrices type(sr_matrix_tensor), dimension(:), allocatable :: Hts !if(present(errst)) errst = 0 ! Tolerance of GMRES gmrestol = 10.0_rKind**(-12) ! Read in convergence parameters call read(Cps, IOObj%infname, unit=cpunit) nchis = size(Cps, 1) whichchi = 1 allocate(MyObs%correlationLengths(1)) ! First representation of the iMPS / initialization of the MPS ! ============================================================ ! Get a representation of the first unit cell via iMPS. warmup_bond_dimension = Cps(1)%max_bond_dimension warmup_tol = Cps(1)%local_tol vtsave = Cps(1)%conv_tol if(Cps(1)%local_tol < 0.0_rKind) then variance_tol = 0.0_rKind else variance_tol = Cps(1)%conv_tol end if ! Never have quantum numbers here nqs = 0 ! LR are compatible with finite-size algorithms call grow_system(Psi, q, Ham, LR, nqs, qs, IOObj, Cps(1), & errst=errst) !if(prop_error('InfiniteMPS_mps: grow_system failed', & ! 'iMPSOps_include.f90:1884', errst=errst)) return ! Refine guess from iMPS with a fMPS calculation ! ----------------------------------------------- ! Build the two site MPO matrices allocate(Hts(q - 1)) do ii = 1, (q - 1) call sdot(Hts(ii), Ham%Ws(ii), Ham%Ws(ii + 1)) end do ! Calculate ground state call find_groundstate_two(Psi, Hts, Ham, LR, Cps(1), energy, & converged, variance, pbc, errst=errst) !if(prop_error('InfiniteMPS_mps : find_groundstate_two '//& ! 'failed.', 'iMPSOps_include.f90:1899', errst=errst)) return ! Delete LR from finite-size do ii = 1, Psi%ll call destroy(LR(ii)) end do deallocate(LR) do ii = 1, (Psi%ll - 1) call destroy(Hts(ii)) end do deallocate(Hts) variance_tol = vtsave if(verbose > 0) write(slog, *) 'energy density from gs', & energy / (q * 1.0_rKind) ! The output from Ground state is in mixed canonical form at site floor(q/2). ! We now extract the orthogonality center into a diagonal matrix \Lambda with ! no (new) error call contr(Theta, Psi%Aa(Psi%oc), Psi%Aa(Psi%oc + 1), [3], [1], & errst=errst) !if(prop_error('InfiniteMPS_mps : contr failed.', & ! 'iMPSOps_include.f90:1923', errst=errst)) return call destroy(Psi%Aa(Psi%oc)) call destroy(Psi%Aa(Psi%oc + 1)) if(Psi%haslambda(Psi%oc + 1)) call destroy(Psi%Lambda(Psi%oc + 1)) ! To-Do: set chi call svd(Psi%Aa(Psi%oc), Psi%Lambda(Psi%oc + 1), Psi%Aa(Psi%oc + 1), & Theta, [1, 2], [3, 4], errst=errst) !if(prop_error('InfiniteMPS_mps : svd failed.', & ! 'iMPSOps_include.f90:1933', errst=errst)) return call destroy(Theta) call create_diag(Lastlam, Psi%Lambda(Psi%oc + 1), errst=errst) !if(prop_error('InfiniteMPS_mps : svd failed.', & ! 'iMPSOps_include.f90:1939', errst=errst)) return ! Shift the zero of energy call shift(Ham%Wl, energy / (q * 1.0_rKind)) call shift(Ham%Wb, energy / (q * 1.0_rKind)) call shift(Ham%Wr, energy / (q * 1.0_rKind)) ! initial environments and new LR overlap allocate(LLLE%Li(1), LRE%Li(1), LR(Psi%ll + 1)) call create(LLLE%Li(1), [1, 1], init='1') call create(LRE%Li(1), [1, 1], init='1') ! Set up LR(1) call ptm_right_mpo(LR(1), Psi%Aa(1), Ham%Wl, Psi%Aa(1), .false., & Matin=LLLE, errst=errst) !if(prop_error('InfiniteMPS_mps : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1955', errst=errst)) return call destroy(LLLE) do ii = 2, Psi%oc call ptm_right_mpo(LLLE, Psi%Aa(ii), Ham%Wb, Psi%Aa(ii), .false., & Matin=LR(1), errst=errst) !if(prop_error('InfiniteMPS_mps : ptm_right_mpo '//& ! 'failed.', 'iMPSOps_include.f90:1963', errst=errst)) return call destroy(LR(1)) call copy(LR(1), LLLE) call destroy(LLLE) end do call ptm_left_mpo(LR(Psi%ll + 1), Psi%Aa(Psi%ll), Ham%Wr, Psi%Aa(Psi%ll), & .false., Matin=LRE, errst=errst) !if(prop_error('InfiniteMPS_mps ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1973', errst=errst)) return call destroy(LRE) do ii = (Psi%ll - 1), (Psi%oc + 1), (-1) call ptm_left_mpo(LRE, Psi%Aa(ii), Ham%Wb, Psi%Aa(ii), & .false., Matin=LR(Psi%ll + 1), errst=errst) !if(prop_error('InfiniteMPS_mps : ptm_left_mpo '//& ! 'failed.', 'iMPSOps_include.f90:1981', errst=errst)) return call destroy(LR(Psi%ll + 1)) call copy(LR(Psi%ll + 1), LRE) call destroy(LRE) end do ! LR(1) and LR(L+1) are now the new boundary environments ! save them for future use call copy(LLLE, LR(1)) call copy(LRE, LR(Psi%ll + 1)) ! Shift MPOs back call shift(Ham%Wl, -energy / (q * 1.0_rKind)) call shift(Ham%Wb, -energy / (q * 1.0_rKind)) call shift(Ham%Wr, -energy / (q * 1.0_rKind)) call destroy(Psi) ! 2nd step: iMPS with environment (iterative part) ! ================================================ ! ! * uses LR, LLLE, LLR from last part ! Run iMPS with this fixed environment call IMPSWithEnvironment(Psi, Ham, q, LR, Cps(1), errst=errst) !if(prop_error('InfiniteMPS_mps : impswithenv failed.', & ! 'iMPSOps_include.f90:2007', errst=errst)) return ! Refine with a finite-size calculation? (min_num_sweeps sweeps) CALL TIGS(psi, Ham, LR, Cps(1), energy, err) !IF(Verbose.gt.0) PRINT *, 'energy density from tigs',energy/(q*1.0_rKind) call prepare(Psi, LR, LLLE, LRE, Ham, energy, Nextlam, Lastlam, numleft, & fl, Cps(1)%max_bond_dimension, errst=errst) !if(prop_error('InfiniteMPS_mps : prepare failed.', & ! 'iMPSOps_include.f90:2016', errst=errst)) return nbelow = 0 do while(whichchi <= nchis) ifail = .true. nbelow = 0 conver = .false. do ninner = 1, Cps(whichchi)%max_imps_iter call tigs(Psi, Ham, LR, Cps(whichchi), energy, err, errst=errst) !if(prop_error('InfiniteMPS_mps : tigs failed.', & ! 'iMPSOps_include.f90:2027', errst=errst)) return call orthogonalityFidelity(Psi, of, Lastlam) if(verbose > 0) write(slog, *) 'energy density', & energy / (q * 1.0_rKind) if(verbose > 0) write(slog, *) 'iteration #, '//& '1-Orthogonality fidelity, truncation density, bd', & ninner, 1.0_rKind - of, err / (q * 1.0_rKind), & Psi%Aa(1)%dl(1) if(err > numzero) then oftol = err / (q * 1.0_rKind) else oftol = variance_tol end if if(abs(1.0_rKind-of) < oftol) then if(verbose > 0) write(slog, *) 'iMPS converged with'//& ' bond dimension, 1-Orthogonality fidelity, '//& 'truncation density', Cps(whichchi)%max_bond_dimension, & 1.0_rKind - of, err / (q * 1.0_rKind) nbelow = nbelow + 1 if(nbelow > 10) then ifail = .false. conver = .true. exit end if end if if(ninner == Cps(whichchi)%max_imps_iter) exit call prepare(Psi, LR, LLLE, LRE, Ham, energy, Nextlam, Lastlam, & numleft, fl, Cps(whichchi)%max_bond_dimension, & errst=errst) !if(prop_error('InfiniteMPS_mps : prepare failed.', & ! 'iMPSOps_include.f90:2064', errst=errst)) return end do oftol = max(oftol, abs(1.0_rKind - of)) CALL Orthogonalize(Psi, Cps(whichchi)%max_bond_dimension, ndeg, & Xs, Ys, LambdaRs, lambdaRinvs, errcode, lastlam, & MyObs%correlationLengths, errst=errst) !if(prop_error('InfiniteMPS_mps : ortho'//& ! 'gonalize failed.', 'iMPSOps_include.f90:2073', & ! errst=errst)) return if(errcode == 0) then call leftorthogonalize(Psi, Psic, Xs, Ys, LambdaRinvs, & errst=errst) !if(prop_error('InfiniteMPS_mps : leftortho'//& ! 'gonalize failed.', 'iMPSOps_include.f90:2080', & ! errst=errst)) return obsname = io_get_obs(IOObj, 0, whichchi) call observe(Psic, ndeg, LambdaRs, Operators, MyObs, & obsname, obsunit, energy, of, & conver, Imapper, Cps(whichchi), errcode, & err, oftol, errst=errst) !if(prop_error('InfiniteMPS_mps : observe '//& ! 'failed.', 'iMPSOps_include.f90:2089', & ! errst=errst)) return do nbelow = 1, size(Psic) call destroy(Psic(nbelow)) call destroy(Xs(nbelow)) call destroy(Ys(nbelow)) call destroy(LambdaRs(nbelow)) call destroy(LambdaRinvs(nbelow)) end do deallocate(Psic, Xs, Ys, LambdaRs, LambdaRinvs) else obsname = io_get_obs(IOObj, 0, whichchi) call observe(Psic, ndeg, LambdaRs, Operators, MyObs, & obsname, obsunit, energy, of, & conver, Imapper, Cps(whichchi), errcode, & err, oftol, errst=errst) !if(prop_error('InfiniteMPS_mps : observe '//& ! 'failed.', 'iMPSOps_include.f90:2108', & ! errst=errst)) return end if whichchi = whichchi + 1 if(whichchi > nchis) exit ! If continuing on, construct the next guess call prepare(Psi, LR, LLLE, LRE, Ham, energy, Nextlam, Lastlam, & numleft, fl, Cps(whichchi)%max_bond_dimension, & errst=errst) !if(prop_error('InfiniteMPS_mps: prepare failed', & ! 'iMPSOps_include.f90:2120', errst=errst)) return end do call destroy(LLLE) call destroy(LRE) call destroy(Psi) call destroy(Lastlam) deallocate(MyObs%correlationLengths) call delete_file(IOObj%convname, cpunit) end subroutine InfiniteMPS_mps
- iMPSOps_f90.InfiniteMPS_mpsc()[source]¶
fortran-subroutine - ?? () Use the infinite size algorithm to find the fixed point in the infinite size limit.
Arguments
- HTYPE(MPO), inout
containing the Hamiltonian of the system.
- qINTEGER, inout
Most probably the length of the unit cell
- OperatorsTYPE(matrixList), inout
List of all the operators used in the Hamiltonian and measurements
- MyObsTYPE(obsc), inout
Settings with the observables to be measured
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
The infinite MPS algorithm is described in I.P. McCulloch’s paper “Infinite size density renormalization group, revisited”, arXiv0804.2509
Source Code
show / hide f90 codesubroutine InfiniteMPS_mpsc(Ham, q, Operators, MyObs, & IOObj, Imapper, pbc, errst) use ioops, only : cpunit, obsunit type(mpoc), intent(inout) :: Ham integer, intent(in) :: q type(tensorlistc) :: Operators type(obsc) :: MyObs type(IOObject), intent(in) :: IOObj type(imap), intent(in) :: Imapper logical, intent(in) :: pbc integer, intent(out), optional :: errst ! Local variables ! --------------- ! for looping integer :: ii ! local convergence parameter warmup chi integer :: warmup_bond_dimension ! arrays for quantum numbers integer, dimension(2) :: nqs integer, dimension(0) :: qs ! local convergence parameter variance tol / warmup_tol real(KIND=rKind) :: variance_tol, warmup_tol ! Filename for measurement character(len=132) :: obsname REAL(KIND=rKind) :: gmrestol TYPE(mpsc) :: psi TYPE(mpsc), POINTER :: psic(:) TYPE(tensorlistc) :: LLLE, LRE TYPE(tensorlistc), dimension(:), allocatable :: LR ! In the basis we work this contains only real values on the diagonal. ! If you choose to work in another basis, this would be a dense matrix. ! Using complex one is as well the most general case. Allover there is ! some overhead here. TYPE(tensorc) :: lastlam ! Since nextlam is a copy of lastlam, the same arguments apply here TYPE(tensorc) :: nextlam TYPE(tensorc), POINTER :: XS(:), Ys(:), lambdaRs(:), lambdaRinvs(:) REAL(KIND=rKind) :: zip, energy, err, of, oftol, variance, vtsave INTEGER :: nchis, whichchi INTEGER :: i INTEGER :: ninner, errcode LOGICAL :: ifail, conver,converged, fl INTEGER :: nbelow, numleft, ndeg ! Two-site tensor type(tensorc) :: Theta ! convergence parameters type(ConvParam), dimension(:), allocatable :: Cps ! All two-site MPO matrices type(sr_matrix_tensorc), dimension(:), allocatable :: Hts !if(present(errst)) errst = 0 ! Tolerance of GMRES gmrestol = 10.0_rKind**(-12) ! Read in convergence parameters call read(Cps, IOObj%infname, unit=cpunit) nchis = size(Cps, 1) whichchi = 1 allocate(MyObs%correlationLengths(1)) ! First representation of the iMPS / initialization of the MPS ! ============================================================ ! Get a representation of the first unit cell via iMPS. warmup_bond_dimension = Cps(1)%max_bond_dimension warmup_tol = Cps(1)%local_tol vtsave = Cps(1)%conv_tol if(Cps(1)%local_tol < 0.0_rKind) then variance_tol = 0.0_rKind else variance_tol = Cps(1)%conv_tol end if ! Never have quantum numbers here nqs = 0 ! LR are compatible with finite-size algorithms call grow_system(Psi, q, Ham, LR, nqs, qs, IOObj, Cps(1), & errst=errst) !if(prop_error('InfiniteMPS_mpsc: grow_system failed', & ! 'iMPSOps_include.f90:1884', errst=errst)) return ! Refine guess from iMPS with a fMPS calculation ! ----------------------------------------------- ! Build the two site MPO matrices allocate(Hts(q - 1)) do ii = 1, (q - 1) call sdot(Hts(ii), Ham%Ws(ii), Ham%Ws(ii + 1)) end do ! Calculate ground state call find_groundstate_two(Psi, Hts, Ham, LR, Cps(1), energy, & converged, variance, pbc, errst=errst) !if(prop_error('InfiniteMPS_mpsc : find_groundstate_two '//& ! 'failed.', 'iMPSOps_include.f90:1899', errst=errst)) return ! Delete LR from finite-size do ii = 1, Psi%ll call destroy(LR(ii)) end do deallocate(LR) do ii = 1, (Psi%ll - 1) call destroy(Hts(ii)) end do deallocate(Hts) variance_tol = vtsave if(verbose > 0) write(slog, *) 'energy density from gs', & energy / (q * 1.0_rKind) ! The output from Ground state is in mixed canonical form at site floor(q/2). ! We now extract the orthogonality center into a diagonal matrix \Lambda with ! no (new) error call contr(Theta, Psi%Aa(Psi%oc), Psi%Aa(Psi%oc + 1), [3], [1], & errst=errst) !if(prop_error('InfiniteMPS_mpsc : contr failed.', & ! 'iMPSOps_include.f90:1923', errst=errst)) return call destroy(Psi%Aa(Psi%oc)) call destroy(Psi%Aa(Psi%oc + 1)) if(Psi%haslambda(Psi%oc + 1)) call destroy(Psi%Lambda(Psi%oc + 1)) ! To-Do: set chi call svd(Psi%Aa(Psi%oc), Psi%Lambda(Psi%oc + 1), Psi%Aa(Psi%oc + 1), & Theta, [1, 2], [3, 4], errst=errst) !if(prop_error('InfiniteMPS_mpsc : svd failed.', & ! 'iMPSOps_include.f90:1933', errst=errst)) return call destroy(Theta) call create_diag(Lastlam, Psi%Lambda(Psi%oc + 1), errst=errst) !if(prop_error('InfiniteMPS_mpsc : svd failed.', & ! 'iMPSOps_include.f90:1939', errst=errst)) return ! Shift the zero of energy call shift(Ham%Wl, energy / (q * 1.0_rKind)) call shift(Ham%Wb, energy / (q * 1.0_rKind)) call shift(Ham%Wr, energy / (q * 1.0_rKind)) ! initial environments and new LR overlap allocate(LLLE%Li(1), LRE%Li(1), LR(Psi%ll + 1)) call create(LLLE%Li(1), [1, 1], init='1') call create(LRE%Li(1), [1, 1], init='1') ! Set up LR(1) call ptm_right_mpo(LR(1), Psi%Aa(1), Ham%Wl, Psi%Aa(1), .false., & Matin=LLLE, errst=errst) !if(prop_error('InfiniteMPS_mpsc : ptm_right_mpo failed.', & ! 'iMPSOps_include.f90:1955', errst=errst)) return call destroy(LLLE) do ii = 2, Psi%oc call ptm_right_mpo(LLLE, Psi%Aa(ii), Ham%Wb, Psi%Aa(ii), .false., & Matin=LR(1), errst=errst) !if(prop_error('InfiniteMPS_mpsc : ptm_right_mpo '//& ! 'failed.', 'iMPSOps_include.f90:1963', errst=errst)) return call destroy(LR(1)) call copy(LR(1), LLLE) call destroy(LLLE) end do call ptm_left_mpo(LR(Psi%ll + 1), Psi%Aa(Psi%ll), Ham%Wr, Psi%Aa(Psi%ll), & .false., Matin=LRE, errst=errst) !if(prop_error('InfiniteMPS_mpsc ptm_left_mpo failed.', & ! 'iMPSOps_include.f90:1973', errst=errst)) return call destroy(LRE) do ii = (Psi%ll - 1), (Psi%oc + 1), (-1) call ptm_left_mpo(LRE, Psi%Aa(ii), Ham%Wb, Psi%Aa(ii), & .false., Matin=LR(Psi%ll + 1), errst=errst) !if(prop_error('InfiniteMPS_mpsc : ptm_left_mpo '//& ! 'failed.', 'iMPSOps_include.f90:1981', errst=errst)) return call destroy(LR(Psi%ll + 1)) call copy(LR(Psi%ll + 1), LRE) call destroy(LRE) end do ! LR(1) and LR(L+1) are now the new boundary environments ! save them for future use call copy(LLLE, LR(1)) call copy(LRE, LR(Psi%ll + 1)) ! Shift MPOs back call shift(Ham%Wl, -energy / (q * 1.0_rKind)) call shift(Ham%Wb, -energy / (q * 1.0_rKind)) call shift(Ham%Wr, -energy / (q * 1.0_rKind)) call destroy(Psi) ! 2nd step: iMPS with environment (iterative part) ! ================================================ ! ! * uses LR, LLLE, LLR from last part ! Run iMPS with this fixed environment call IMPSWithEnvironment(Psi, Ham, q, LR, Cps(1), errst=errst) !if(prop_error('InfiniteMPS_mpsc : impswithenv failed.', & ! 'iMPSOps_include.f90:2007', errst=errst)) return ! Refine with a finite-size calculation? (min_num_sweeps sweeps) CALL TIGS(psi, Ham, LR, Cps(1), energy, err) !IF(Verbose.gt.0) PRINT *, 'energy density from tigs',energy/(q*1.0_rKind) call prepare(Psi, LR, LLLE, LRE, Ham, energy, Nextlam, Lastlam, numleft, & fl, Cps(1)%max_bond_dimension, errst=errst) !if(prop_error('InfiniteMPS_mpsc : prepare failed.', & ! 'iMPSOps_include.f90:2016', errst=errst)) return nbelow = 0 do while(whichchi <= nchis) ifail = .true. nbelow = 0 conver = .false. do ninner = 1, Cps(whichchi)%max_imps_iter call tigs(Psi, Ham, LR, Cps(whichchi), energy, err, errst=errst) !if(prop_error('InfiniteMPS_mpsc : tigs failed.', & ! 'iMPSOps_include.f90:2027', errst=errst)) return call orthogonalityFidelity(Psi, of, Lastlam) if(verbose > 0) write(slog, *) 'energy density', & energy / (q * 1.0_rKind) if(verbose > 0) write(slog, *) 'iteration #, '//& '1-Orthogonality fidelity, truncation density, bd', & ninner, 1.0_rKind - of, err / (q * 1.0_rKind), & Psi%Aa(1)%dl(1) if(err > numzero) then oftol = err / (q * 1.0_rKind) else oftol = variance_tol end if if(abs(1.0_rKind-of) < oftol) then if(verbose > 0) write(slog, *) 'iMPS converged with'//& ' bond dimension, 1-Orthogonality fidelity, '//& 'truncation density', Cps(whichchi)%max_bond_dimension, & 1.0_rKind - of, err / (q * 1.0_rKind) nbelow = nbelow + 1 if(nbelow > 10) then ifail = .false. conver = .true. exit end if end if if(ninner == Cps(whichchi)%max_imps_iter) exit call prepare(Psi, LR, LLLE, LRE, Ham, energy, Nextlam, Lastlam, & numleft, fl, Cps(whichchi)%max_bond_dimension, & errst=errst) !if(prop_error('InfiniteMPS_mpsc : prepare failed.', & ! 'iMPSOps_include.f90:2064', errst=errst)) return end do oftol = max(oftol, abs(1.0_rKind - of)) CALL Orthogonalize(Psi, Cps(whichchi)%max_bond_dimension, ndeg, & Xs, Ys, LambdaRs, lambdaRinvs, errcode, lastlam, & MyObs%correlationLengths, errst=errst) !if(prop_error('InfiniteMPS_mpsc : ortho'//& ! 'gonalize failed.', 'iMPSOps_include.f90:2073', & ! errst=errst)) return if(errcode == 0) then call leftorthogonalize(Psi, Psic, Xs, Ys, LambdaRinvs, & errst=errst) !if(prop_error('InfiniteMPS_mpsc : leftortho'//& ! 'gonalize failed.', 'iMPSOps_include.f90:2080', & ! errst=errst)) return obsname = io_get_obs(IOObj, 0, whichchi) call observe(Psic, ndeg, LambdaRs, Operators, MyObs, & obsname, obsunit, energy, of, & conver, Imapper, Cps(whichchi), errcode, & err, oftol, errst=errst) !if(prop_error('InfiniteMPS_mpsc : observe '//& ! 'failed.', 'iMPSOps_include.f90:2089', & ! errst=errst)) return do nbelow = 1, size(Psic) call destroy(Psic(nbelow)) call destroy(Xs(nbelow)) call destroy(Ys(nbelow)) call destroy(LambdaRs(nbelow)) call destroy(LambdaRinvs(nbelow)) end do deallocate(Psic, Xs, Ys, LambdaRs, LambdaRinvs) else obsname = io_get_obs(IOObj, 0, whichchi) call observe(Psic, ndeg, LambdaRs, Operators, MyObs, & obsname, obsunit, energy, of, & conver, Imapper, Cps(whichchi), errcode, & err, oftol, errst=errst) !if(prop_error('InfiniteMPS_mpsc : observe '//& ! 'failed.', 'iMPSOps_include.f90:2108', & ! errst=errst)) return end if whichchi = whichchi + 1 if(whichchi > nchis) exit ! If continuing on, construct the next guess call prepare(Psi, LR, LLLE, LRE, Ham, energy, Nextlam, Lastlam, & numleft, fl, Cps(whichchi)%max_bond_dimension, & errst=errst) !if(prop_error('InfiniteMPS_mpsc: prepare failed', & ! 'iMPSOps_include.f90:2120', errst=errst)) return end do call destroy(LLLE) call destroy(LRE) call destroy(Psi) call destroy(Lastlam) deallocate(MyObs%correlationLengths) call delete_file(IOObj%convname, cpunit) end subroutine InfiniteMPS_mpsc
- iMPSOps_f90.ansatz_left_tensor()[source]¶
fortran-subroutine - June 2018 (dj, extracted from larger subroutine) Creating an educated guess for one of the new inner sites using McCulloch’s prediction algorithm.
Arguments
- PsiTYPE(tensor), inout
On exit, the educated guess.
- LamTYPE(tensor), in
Singular values.
- PhiTYPE(tensor), in
Existing tensor required to construct initial guess.
Details
The initial guess construct is A-> Lambda[n-1] B[n-1].
Source Code
show / hide f90 codesubroutine ansatz_left_tensor(Psi, Lam, Phi, errst) type(tensor), intent(inout) :: Psi type(tensor), intent(in) :: Lam type(tensor), intent(in) :: Phi integer, intent(out), optional :: errst ! No local variables ! ------------------ !if(present(errst)) errst = 0 call copy(Psi, Phi) call contr_diag(Psi, Lam, 1, errst=errst) !if(prop_error('ansatz_left_tensor: '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:2186', & ! errst=errst)) return end subroutine ansatz_left_tensor
- iMPSOps_f90.ansatz_right_tensor()[source]¶
fortran-subroutine - June 2018 (dj, extracted from larger subroutine) Creating an educated guess for one of the new inner sites using McCulloch’s prediction algorithm.
Arguments
- PsiTYPE(tensor), inout
On exit, the educated guess.
- LamTYPE(tensor), in
Singular values.
- PhiTYPE(tensor), in
Existing tensor required to construct initial guess.
Details
The initial guess construct is B-> Lambda[n-2]^{-1} A[n-1] Lambda[N-1]
Source Code
show / hide f90 codesubroutine ansatz_right_tensor(Psi, Lam, Laminv, Phi, errst) type(tensor), intent(inout) :: Psi type(tensor), intent(in) :: Lam, Laminv type(tensor), intent(inout) :: Phi integer, intent(out), optional :: errst ! Local variables ! --------------- type(tensor) :: Vec call copy(Psi, Phi) call copy(Vec, Laminv) Vec%elem = 1.0_rKind / Vec%elem call contr_diag(Psi, Lam, 3, errst=errst) !if(prop_error('ansatz_right_tensor: '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:2244', & ! errst=errst)) return call contr_diag(Psi, Vec, 1, errst=errst) !if(prop_error('ansatz_right_tensor: '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:2249', & ! errst=errst)) return call destroy(Vec) end subroutine ansatz_right_tensor
- iMPSOps_f90.ansatz_left_tensorc()[source]¶
fortran-subroutine - June 2018 (dj, extracted from larger subroutine) Creating an educated guess for one of the new inner sites using McCulloch’s prediction algorithm.
Arguments
- PsiTYPE(tensorc), inout
On exit, the educated guess.
- LamTYPE(tensor), in
Singular values.
- PhiTYPE(tensorc), in
Existing tensor required to construct initial guess.
Details
The initial guess construct is A-> Lambda[n-1] B[n-1].
Source Code
show / hide f90 codesubroutine ansatz_left_tensorc(Psi, Lam, Phi, errst) type(tensorc), intent(inout) :: Psi type(tensor), intent(in) :: Lam type(tensorc), intent(in) :: Phi integer, intent(out), optional :: errst ! No local variables ! ------------------ !if(present(errst)) errst = 0 call copy(Psi, Phi) call contr_diag(Psi, Lam, 1, errst=errst) !if(prop_error('ansatz_left_tensorc: '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:2186', & ! errst=errst)) return end subroutine ansatz_left_tensorc
- iMPSOps_f90.ansatz_right_tensorc()[source]¶
fortran-subroutine - June 2018 (dj, extracted from larger subroutine) Creating an educated guess for one of the new inner sites using McCulloch’s prediction algorithm.
Arguments
- PsiTYPE(tensorc), inout
On exit, the educated guess.
- LamTYPE(tensor), in
Singular values.
- PhiTYPE(tensorc), in
Existing tensor required to construct initial guess.
Details
The initial guess construct is B-> Lambda[n-2]^{-1} A[n-1] Lambda[N-1]
Source Code
show / hide f90 codesubroutine ansatz_right_tensorc(Psi, Lam, Laminv, Phi, errst) type(tensorc), intent(inout) :: Psi type(tensor), intent(in) :: Lam, Laminv type(tensorc), intent(inout) :: Phi integer, intent(out), optional :: errst ! Local variables ! --------------- type(tensor) :: Vec call copy(Psi, Phi) call copy(Vec, Laminv) Vec%elem = 1.0_rKind / Vec%elem call contr_diag(Psi, Lam, 3, errst=errst) !if(prop_error('ansatz_right_tensorc: '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:2244', & ! errst=errst)) return call contr_diag(Psi, Vec, 1, errst=errst) !if(prop_error('ansatz_right_tensorc: '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:2249', & ! errst=errst)) return call destroy(Vec) end subroutine ansatz_right_tensorc
- iMPSOps_f90.IMPSWithEnvironment_mps()[source]¶
fortran-subroutine - ?? () Use iMPS to solve a system with a fixed enviroment.
Arguments
- psiTYPE(mps), out
on exit MPS
- HTYPE(mpo), inout
Hamiltonian
- LINTEGER, in
Number of sites in the MPS
- maxbondDINTEGER, in
maximal bond dimension for the MPS
- LRTYPE(tensorlist), inout
??
Source Code
show / hide f90 codesubroutine IMPSWithEnvironment_mps(Psi, H, ll, LR, Cp, errst) type(mps), intent(out) :: Psi type(mpo) :: H integer, intent(in) :: ll type(tensorlist), dimension(:), intent(inout) :: LR type(ConvParam), intent(in) :: Cp integer, intent(out), optional :: errst ! Local variables ! --------------- ! bond dimension of theta two-site tensor integer, dimension(4) :: thetadl type(sr_matrix_tensor) :: TW ! For storing eigenvalues values type(tensor) :: Eigvals ! short-cut maximal bond dimension integer :: maxbondd real(KIND=rKind) :: err, tolin logical :: singlesite integer :: n, niter, counter, i, dl, d, dr, alpha, beta, effBD ! Two-site tensor type(tensor) :: Theta ! Singular values type(tensor) :: Lam singlesite = .not. (mod(ll, 2) == 0) if(singlesite) then niter = floor(0.5_rKind * ll) call create(Eigvals, [niter + 1]) else niter = floor(0.5_rKind * ll) call create(Eigvals, [niter]) end if maxbondd = Cp%max_bond_dimension if(Cp%local_tol < 0.0_rKind) then tolin = 0.0_rKind else tolin = Cp%local_tol end if Psi%ll = ll allocate(Psi%Aa(ll), Psi%haslambda(ll + 1), Psi%Lambda(ll + 1), & Psi%can(ll)) Psi%haslambda = .false. Psi%can = 'o' effbd = 1 ! Two-site Hamiltonian for complete subroutine call sdot(TW, H%Wb, H%Wb) ! 1) Initialization of the iMPS ! ----------------------------- n = 0 ! Create a random guess at the two-site MPS dl = LR(1)%Li(1)%dl(2) d = H%Wb%Row(1)%Op(1)%dl(1) dr = LR(ll + 1)%Li(1)%dl(1) call create(Theta, [dl, d, d, dr], init='R') call scale(1.0_rKind / sqrt(norm(Theta)), Theta) call lanczos(LR(n + 1), TW, LR(ll - n + 1), Eigvals%elem(n + 1), & Theta, .false., .false., Cp%max_num_lanczos_iter, & Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mps : lanczos failed.', & ! 'iMPSOps_include.f90:2384', errst=errst)) return call split(Psi%Aa(n + 1), Psi%Lambda(n + 2), Psi%Aa(ll - n), Theta, & [1, 2], [3, 4], trunc=tolin, ncut=maxbondd, err=err, & method='Y', errst=errst) !if(prop_error('IMPSWithEnvironment_mps : split failed.', & ! 'iMPSOps_include.f90:2390', errst=errst)) return if(ll - n /= n + 2) then call copy(Psi%Lambda(ll - n), Psi%Lambda(n + 2)) end if Psi%haslambda(n + 2) = .true. Psi%haslambda(ll - n) = .true. Psi%can(n + 1) = 'l' Psi%can(ll - n) = 'r' call destroy(Theta) ! find effective bond dimension effbd = max(effbd, Psi%Aa(n + 1)%dl(3)) if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & Eigvals%elem(n + 1) / (2 * (n + 1)) ! 2) Second iteration ! ------------------- n = 1 if(ll > 3) then dl = effBd dr = dl * d ! Add optimized sites to overlaps call ptm_right_mpo(LR(n + 1), Psi%Aa(n), H%Wb, Psi%Aa(n), & .false., Matin=LR(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ptm_right'//& ! '_mpo failed.', 'iMPSOps_include.f90:2421', errst=errst)) return call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 1), H%Wb, & Psi%Aa(ll - n + 1), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2427', errst=errst)) return ! Create a random guess at the two-site MPS thetadl = [min(dl, effbd), d, d, min(dl, effbd)] call create(Theta, thetadl, init='R') call scale(1.0_rKind / sqrt(norm(Theta)), Theta) call lanczos(LR(n + 1), TW, LR(ll - n + 1), Eigvals%elem(n + 1), & Theta, .false., .false., Cp%max_num_lanczos_iter, & Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mps : lanczos '//& ! 'failed.', 'iMPSOps_include.f90:2438', errst=errst)) return call split(Psi%Aa(n + 1), Psi%Lambda(n + 2), Psi%Aa(ll - n), & Theta, [1, 2], [3, 4], trunc=tolin, ncut=maxbondd, & err=err, method='Y', errst=errst) !if(prop_error('IMPSWithEnvironment_mps : split '//& ! 'failed.', 'iMPSOps_include.f90:2444', errst=errst)) return if(n + 2 /= ll - n) call copy(Psi%Lambda(ll - n), Psi%Lambda(n + 2)) Psi%haslambda(n + 2) = .true. Psi%haslambda(ll - n) = .true. Psi%can(n + 1) = 'l' Psi%can(ll - n) = 'r' call destroy(Theta) ! find effective bond dimension effbd = max(effbd, Psi%Aa(n + 1)%dl(3)) if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & Eigvals%elem(n + 1) / (2 * (n + 1)) end if ! 3) Iterative part of the algorithm ! ---------------------------------- do n = 2, (niter - 1) ! Add optimized sites to overlaps call ptm_right_mpo(LR(n + 1), Psi%Aa(n), H%Wb, Psi%Aa(n), & .false., Matin=LR(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ptm_right'//& ! '_mpo failed.', 'iMPSOps_include.f90:2472', errst=errst)) return call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 2), H%Wb, & Psi%Aa(ll - n + 2), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2478', errst=errst)) return ! Create an educated guess for the two inner sites using ! McCulloch's prediction algorithm call ansatz_left(Psi%Aa(n + 1), Psi%Lambda(ll - n + 1), & Psi%Aa(ll - n + 1), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ansatz'//& ! '_left failed.', 'iMPSOps_include.f90:2485', & ! errst=errst)) return call ansatz_right(Psi%Aa(ll - n), Psi%Lambda(n), Psi%Lambda(n-1), & Psi%Aa(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ansatz'//& ! '_right failed.', 'iMPSOps_include.f90:2491', & ! errst=errst)) return call contr(Theta, Psi%Aa(n + 1), Psi%Aa(ll - n), [3], [1], & errst=errst) !if(prop_error('IMPSWithEnvironment_mps : contr '//& ! 'failed.', 'iMPSOps_include.f90:2497', errst=errst)) return call scale(1.0_rKind / sqrt(norm(Theta)), Theta) call lanczos(LR(n + 1), TW, LR(ll - n + 1), Eigvals%elem(n + 1), & Theta, .false., .false., Cp%max_num_lanczos_iter, & Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mps : lanczos '//& ! 'failed.', 'iMPSOps_include.f90:2505', errst=errst)) return call split(Psi%Aa(n + 1), Psi%Lambda(n + 2), Psi%Aa(ll - n), & Theta, [1, 2], [3, 4], trunc=tolin, ncut=maxbondd, & err=err, method='Y', errst=errst) !if(prop_error('IMPSWithEnvironment_mps : split '//& ! 'failed.', 'iMPSOps_include.f90:2511', errst=errst)) return if(n /= niter - 1) call copy(Psi%Lambda(ll - n), Psi%Lambda(n + 2)) Psi%haslambda(n + 2) = .true. Psi%haslambda(ll - n) = .true. Psi%can(n + 1) = 'l' Psi%can(ll - n) = 'r' call destroy(Theta) ! find effective bond dimension effbd = max(effbd, Psi%Aa(n + 1)%dl(3)) if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & Eigvals%elem(n + 1) / (2 * (n + 1)) end do n = niter if(singlesite) then ! Add optimized sites to overlaps call ptm_right_mpo(LR(n + 1), Psi%Aa(n), H%Wb, Psi%Aa(n), & .false., Matin=LR(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ptm_right'//& ! '_mpo failed.', 'iMPSOps_include.f90:2537', errst=errst)) return call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 1), H%Wb, & Psi%Aa(ll - n + 1), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2543', errst=errst)) return dl = Psi%Aa(n)%dl(3) dr = Psi%Aa(ll-n+1)%dl(1) call create(Psi%Aa(n + 1), [dl, d, dr], init='R') call scale(1.0_rKind / sqrt(norm(Psi%Aa(n + 1))), Psi%Aa(n + 1)) call lanczos(LR(n + 1), H%Wb, LR(ll - n + 1), Eigvals%elem(n + 1), & Psi%Aa(n + 1), .false., .false., & Cp%max_num_lanczos_iter, Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mps : lanczos '//& ! 'failed.', 'iMPSOps_include.f90:2555', errst=errst)) return Psi%can(n + 1) = 'c' Psi%oc = n + 1 if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & eigvals%elem(n + 1) / (2 * n + 1) else ! We begin on the left of the two MPS, and so we only ! add the right overlap call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 1), H%Wb, & Psi%Aa(ll - n + 1), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mps : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2571', errst=errst)) return call contr_diag(Psi%Aa(ll / 2), Psi%Lambda(ll / 2 + 1), 3, & errst=errst) !if(prop_error('IMPSWithEnvironment_mps : contr_diag'//& ! ' failed.', 'iMPSOps_include.f90:2576', errst=errst)) return Psi%can(ll / 2) = 'c' Psi%oc = ll / 2 end if call destroy(Eigvals) call destroy(TW) end subroutine IMPSWithEnvironment_mps
- iMPSOps_f90.IMPSWithEnvironment_mpsc()[source]¶
fortran-subroutine - ?? () Use iMPS to solve a system with a fixed enviroment.
Arguments
- psiTYPE(mpsc), out
on exit MPS
- HTYPE(mpoc), inout
Hamiltonian
- LINTEGER, in
Number of sites in the MPS
- maxbondDINTEGER, in
maximal bond dimension for the MPS
- LRTYPE(tensorlistc), inout
??
Source Code
show / hide f90 codesubroutine IMPSWithEnvironment_mpsc(Psi, H, ll, LR, Cp, errst) type(mpsc), intent(out) :: Psi type(mpoc) :: H integer, intent(in) :: ll type(tensorlistc), dimension(:), intent(inout) :: LR type(ConvParam), intent(in) :: Cp integer, intent(out), optional :: errst ! Local variables ! --------------- ! bond dimension of theta two-site tensor integer, dimension(4) :: thetadl type(sr_matrix_tensorc) :: TW ! For storing eigenvalues values type(tensor) :: Eigvals ! short-cut maximal bond dimension integer :: maxbondd real(KIND=rKind) :: err, tolin logical :: singlesite integer :: n, niter, counter, i, dl, d, dr, alpha, beta, effBD ! Two-site tensor type(tensorc) :: Theta ! Singular values type(tensor) :: Lam singlesite = .not. (mod(ll, 2) == 0) if(singlesite) then niter = floor(0.5_rKind * ll) call create(Eigvals, [niter + 1]) else niter = floor(0.5_rKind * ll) call create(Eigvals, [niter]) end if maxbondd = Cp%max_bond_dimension if(Cp%local_tol < 0.0_rKind) then tolin = 0.0_rKind else tolin = Cp%local_tol end if Psi%ll = ll allocate(Psi%Aa(ll), Psi%haslambda(ll + 1), Psi%Lambda(ll + 1), & Psi%can(ll)) Psi%haslambda = .false. Psi%can = 'o' effbd = 1 ! Two-site Hamiltonian for complete subroutine call sdot(TW, H%Wb, H%Wb) ! 1) Initialization of the iMPS ! ----------------------------- n = 0 ! Create a random guess at the two-site MPS dl = LR(1)%Li(1)%dl(2) d = H%Wb%Row(1)%Op(1)%dl(1) dr = LR(ll + 1)%Li(1)%dl(1) call create(Theta, [dl, d, d, dr], init='R') call scale(1.0_rKind / sqrt(norm(Theta)), Theta) call lanczos(LR(n + 1), TW, LR(ll - n + 1), Eigvals%elem(n + 1), & Theta, .false., .false., Cp%max_num_lanczos_iter, & Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : lanczos failed.', & ! 'iMPSOps_include.f90:2384', errst=errst)) return call split(Psi%Aa(n + 1), Psi%Lambda(n + 2), Psi%Aa(ll - n), Theta, & [1, 2], [3, 4], trunc=tolin, ncut=maxbondd, err=err, & method='Y', errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : split failed.', & ! 'iMPSOps_include.f90:2390', errst=errst)) return if(ll - n /= n + 2) then call copy(Psi%Lambda(ll - n), Psi%Lambda(n + 2)) end if Psi%haslambda(n + 2) = .true. Psi%haslambda(ll - n) = .true. Psi%can(n + 1) = 'l' Psi%can(ll - n) = 'r' call destroy(Theta) ! find effective bond dimension effbd = max(effbd, Psi%Aa(n + 1)%dl(3)) if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & Eigvals%elem(n + 1) / (2 * (n + 1)) ! 2) Second iteration ! ------------------- n = 1 if(ll > 3) then dl = effBd dr = dl * d ! Add optimized sites to overlaps call ptm_right_mpo(LR(n + 1), Psi%Aa(n), H%Wb, Psi%Aa(n), & .false., Matin=LR(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ptm_right'//& ! '_mpo failed.', 'iMPSOps_include.f90:2421', errst=errst)) return call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 1), H%Wb, & Psi%Aa(ll - n + 1), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2427', errst=errst)) return ! Create a random guess at the two-site MPS thetadl = [min(dl, effbd), d, d, min(dl, effbd)] call create(Theta, thetadl, init='R') call scale(1.0_rKind / sqrt(norm(Theta)), Theta) call lanczos(LR(n + 1), TW, LR(ll - n + 1), Eigvals%elem(n + 1), & Theta, .false., .false., Cp%max_num_lanczos_iter, & Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : lanczos '//& ! 'failed.', 'iMPSOps_include.f90:2438', errst=errst)) return call split(Psi%Aa(n + 1), Psi%Lambda(n + 2), Psi%Aa(ll - n), & Theta, [1, 2], [3, 4], trunc=tolin, ncut=maxbondd, & err=err, method='Y', errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : split '//& ! 'failed.', 'iMPSOps_include.f90:2444', errst=errst)) return if(n + 2 /= ll - n) call copy(Psi%Lambda(ll - n), Psi%Lambda(n + 2)) Psi%haslambda(n + 2) = .true. Psi%haslambda(ll - n) = .true. Psi%can(n + 1) = 'l' Psi%can(ll - n) = 'r' call destroy(Theta) ! find effective bond dimension effbd = max(effbd, Psi%Aa(n + 1)%dl(3)) if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & Eigvals%elem(n + 1) / (2 * (n + 1)) end if ! 3) Iterative part of the algorithm ! ---------------------------------- do n = 2, (niter - 1) ! Add optimized sites to overlaps call ptm_right_mpo(LR(n + 1), Psi%Aa(n), H%Wb, Psi%Aa(n), & .false., Matin=LR(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ptm_right'//& ! '_mpo failed.', 'iMPSOps_include.f90:2472', errst=errst)) return call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 2), H%Wb, & Psi%Aa(ll - n + 2), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2478', errst=errst)) return ! Create an educated guess for the two inner sites using ! McCulloch's prediction algorithm call ansatz_left(Psi%Aa(n + 1), Psi%Lambda(ll - n + 1), & Psi%Aa(ll - n + 1), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ansatz'//& ! '_left failed.', 'iMPSOps_include.f90:2485', & ! errst=errst)) return call ansatz_right(Psi%Aa(ll - n), Psi%Lambda(n), Psi%Lambda(n-1), & Psi%Aa(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ansatz'//& ! '_right failed.', 'iMPSOps_include.f90:2491', & ! errst=errst)) return call contr(Theta, Psi%Aa(n + 1), Psi%Aa(ll - n), [3], [1], & errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : contr '//& ! 'failed.', 'iMPSOps_include.f90:2497', errst=errst)) return call scale(1.0_rKind / sqrt(norm(Theta)), Theta) call lanczos(LR(n + 1), TW, LR(ll - n + 1), Eigvals%elem(n + 1), & Theta, .false., .false., Cp%max_num_lanczos_iter, & Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : lanczos '//& ! 'failed.', 'iMPSOps_include.f90:2505', errst=errst)) return call split(Psi%Aa(n + 1), Psi%Lambda(n + 2), Psi%Aa(ll - n), & Theta, [1, 2], [3, 4], trunc=tolin, ncut=maxbondd, & err=err, method='Y', errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : split '//& ! 'failed.', 'iMPSOps_include.f90:2511', errst=errst)) return if(n /= niter - 1) call copy(Psi%Lambda(ll - n), Psi%Lambda(n + 2)) Psi%haslambda(n + 2) = .true. Psi%haslambda(ll - n) = .true. Psi%can(n + 1) = 'l' Psi%can(ll - n) = 'r' call destroy(Theta) ! find effective bond dimension effbd = max(effbd, Psi%Aa(n + 1)%dl(3)) if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & Eigvals%elem(n + 1) / (2 * (n + 1)) end do n = niter if(singlesite) then ! Add optimized sites to overlaps call ptm_right_mpo(LR(n + 1), Psi%Aa(n), H%Wb, Psi%Aa(n), & .false., Matin=LR(n), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ptm_right'//& ! '_mpo failed.', 'iMPSOps_include.f90:2537', errst=errst)) return call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 1), H%Wb, & Psi%Aa(ll - n + 1), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2543', errst=errst)) return dl = Psi%Aa(n)%dl(3) dr = Psi%Aa(ll-n+1)%dl(1) call create(Psi%Aa(n + 1), [dl, d, dr], init='R') call scale(1.0_rKind / sqrt(norm(Psi%Aa(n + 1))), Psi%Aa(n + 1)) call lanczos(LR(n + 1), H%Wb, LR(ll - n + 1), Eigvals%elem(n + 1), & Psi%Aa(n + 1), .false., .false., & Cp%max_num_lanczos_iter, Cp%lanczos_tol, errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : lanczos '//& ! 'failed.', 'iMPSOps_include.f90:2555', errst=errst)) return Psi%can(n + 1) = 'c' Psi%oc = n + 1 if(verbose > 0) write(slog, *) 'energy and energy density at '//& 'nth iteration of IMPS=', n, Eigvals%elem(n + 1), & eigvals%elem(n + 1) / (2 * n + 1) else ! We begin on the left of the two MPS, and so we only ! add the right overlap call ptm_left_mpo(LR(ll - n + 1), Psi%Aa(ll - n + 1), H%Wb, & Psi%Aa(ll - n + 1), .false., & Matin=LR(ll - n + 2), errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : ptm_left'//& ! '_mpo failed.', 'iMPSOps_include.f90:2571', errst=errst)) return call contr_diag(Psi%Aa(ll / 2), Psi%Lambda(ll / 2 + 1), 3, & errst=errst) !if(prop_error('IMPSWithEnvironment_mpsc : contr_diag'//& ! ' failed.', 'iMPSOps_include.f90:2576', errst=errst)) return Psi%can(ll / 2) = 'c' Psi%oc = ll / 2 end if call destroy(Eigvals) call destroy(TW) end subroutine IMPSWithEnvironment_mpsc
- iMPSOps_f90.orthogonalize_mps()[source]¶
fortran-subroutine - ?? () Find the set of Xs(i) and Ys(i) corresponding to the dominant left (right) eigenvectors of the left-canonical (right-canonical) unit cells.
Arguments
- LambdaRsTYPE(matrix)(*), out
??? (normalized)
- LambdaRinvsTYPE(matrix)(*), out
unnormalized pseudo-inverse of LambdaRs
- errcodeINTEGER, out
possibly error code from ARPACK, otherwise 1000: ndegL and ndegR are not the same after 10 tries (-400): no hermitian orthnormormal set (-300): problem in conversion from complex to real
Details
The following steps are performed 1) MISSING DESCRIPTION 2) MISSING DESCRIPTION 3) Mark all hermitian matrices with
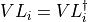 as well
as well
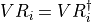 . Assert that these matrices have a
positive trace, so:
. Assert that these matrices have a
positive trace, so:
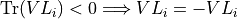 4) Check for all hermitian matrices in an eigenvalue decomposition that
they are positive.
5) Trying to fix situation if there is no pair
4) Check for all hermitian matrices in an eigenvalue decomposition that
they are positive.
5) Trying to fix situation if there is no pair 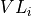 and
and
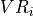 with both hermitian and positive:
with both hermitian and positive:MISSING DESCRIPTION
6) Calculate the overlap matrix of the Frobenius norm
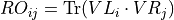 and decompose the
matrix in a SVD
and decompose the
matrix in a SVD 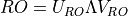 .
TO-DO: THIS IS SYMMETRIC DUE TO TRACE, BUT NOT USED IN CODE (sum possible,
better not replace SVD with eigenvalue until knowing what happens to
negative eigenvalues.
7) Transform to final basis. Assuming all matrices are hermitian positive
the i-th final matrix
.
TO-DO: THIS IS SYMMETRIC DUE TO TRACE, BUT NOT USED IN CODE (sum possible,
better not replace SVD with eigenvalue until knowing what happens to
negative eigenvalues.
7) Transform to final basis. Assuming all matrices are hermitian positive
the i-th final matrix 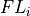 reads like
reads like
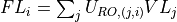 and respectively
and respectively
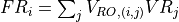 .
8) Assure that all FL, FR have positive trace and assert this if necessary
by multiplying with
.
8) Assure that all FL, FR have positive trace and assert this if necessary
by multiplying with  .
9) Convert back to original type, so real or complex. For the real case we
take
.
9) Convert back to original type, so real or complex. For the real case we
take 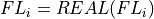 if
if 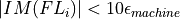 . Analogue for
. Analogue for 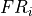 .
.MISSING DESCRIPTION FOR COMPLEX (NOT IMPLEMENTED)
10) Quasi-Cholesky decomposition. For the left side we start with the following step: the eigenvalue decomposition is calculate, such that
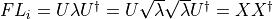 . In general the Cholesky deomposition
would work in this step as well, but in case close to singularity the
eigenvalue decomposition are more stable. The eigenvalue decomposition
on
. In general the Cholesky deomposition
would work in this step as well, but in case close to singularity the
eigenvalue decomposition are more stable. The eigenvalue decomposition
on 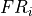 leads to
leads to 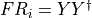 .
Calculate
.
Calculate 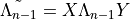 . This
matrix is inverted via the pseudo-inverse defined over the SVD. (A
general matrix
. This
matrix is inverted via the pseudo-inverse defined over the SVD. (A
general matrix 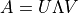 has the pseudo-inverse
has the pseudo-inverse
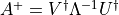 where only
numerical non-zero singular values are considered.)
Finally a normalization is executed
where only
numerical non-zero singular values are considered.)
Finally a normalization is executed 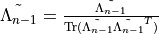 WHY IS PSEUDO-INVERSE NOT NORMALIZED?
WHY IS PSEUDO-INVERSE NOT NORMALIZED?Source Code
show / hide f90 codesubroutine orthogonalize_mps(Psi, maxbondd, ndeg, Xs, Ys, LambdaRs, & lambdaRinvs, errcode, lastlam, correlationLengths, errst) TYPE(mps) :: psi INTEGER :: maxbondD ! unused integer :: ndeg TYPE(tensor), INTENT(OUT), POINTER :: Xs(:), Ys(:) TYPE(tensor), INTENT(OUT), POINTER :: LambdaRs(:), LambdaRinvs(:) INTEGER, INTENT(OUT) :: errcode TYPE(tensor), INTENT(inout) :: lastlam REAL(KIND=rKind), INTENT(OUT) :: correlationLengths(:) integer, intent(out), optional :: errst ! Local variables ! --------------- ! record try for forming a hermitian orthonormal set from the ! degenerate matrices logical :: alreadytried = .false. ! for looping integer :: ii, jj, i, j ! for indexing integer :: kk ! looping/counter for the hermitian positive matrices integer :: lok, rok ! number of tensors in the MPS integer :: q ! number of hermitian and positive pairs of matrices in VL, VR integer :: numok ! check if matrices have positive trace (only local use inside loop) ! Also abused as norm real(KIND=rKind) :: trc ! i-th entry indicates if VL(i) is hermitian and positive (respectively VR(i)) ! .false. is as well set if other R/Liamok is not hermitian positive logical, allocatable :: Liamok(:), Riamok(:) ! logical :: lflag, rflag integer :: ncorr, ndegL, ndegR, lerrcode, rerrcode, k, chi, tried ! temporary scalar real(KIND=rKind) :: sctmp ! working copy of the MPS type(mps) :: psit ! Singular values for all SVDs type(tensor) :: S ! Temporary vector type(tensor) :: Tmpvec ! Unitary matrices for the SVD of the eigenmatrix (always complex) type(tensorc) :: U, V ! Unitary matrices for the SVD of the (real-valued) overlap matrix type(tensor) :: Ur, Vre ! Unitary matrix for remaining type-dependent SVD at the end type(tensor) :: U2, V2 type(tensor), POINTER :: RealVl(:), RealVr(:) type(tensorc), POINTER :: VL(:), VR(:), TransXs(:), TransYs(:) type(tensor) :: roverlapmat ! Temporary tensor type(tensor) :: Rev ! Mixed-canonical state type(tensor) :: E type(tensor) :: evs type(tensor) :: Atmp real(KIND=rKind) :: maxLev, subLev, maxRev, tol, zip, nrm1,nrm2 integer, allocatable :: indx(:) real(KIND=rKind), allocatable :: xis(:), eigw(:), tmp(:) type(tensor), pointer :: VLR(:) !if(present(errst)) errst = 0 q = Psi%ll ! \chi=1 states cause issues, but we know exactly what everything is... if(Psi%Aa(q)%dl(3) == 1) then write(slog, *) 'chi=1 used!' errcode = 0 ndeg = 1 allocate(Xs(ndeg), Ys(ndeg), LambdaRs(ndeg), LambdaRinvs(ndeg)) call create(Xs(1), [1, 1], init='1') call create(Ys(1), [1, 1], init='1') call create(LambdaRs(1), [1, 1], init='1') call create(LambdaRinvs(1), [1, 1], init='1') correlationlengths = 0.0_rKind return end if ncorr = 20 ndegL = 0 ndegR = 1 tried = 0 do while(ndegL .ne. ndegR) ! Take care of left unit cell ! =========================== ! Form left-canonical unit cell call copy(Psit, Psi) ! Append \Lambda^{-1}_{n-1} to form TI unit cell ! Use pseudoinverse for stability tol = Psit%Aa(q)%dl(3) * maxval(real(Lastlam%elem(:Lastlam%dim))) & * numzero call create(Tmpvec, [Lastlam%dl(1)]) kk = 1 do ii = 1, Lastlam%dl(1) if(real(Lastlam%elem(kk)) > tol) then Tmpvec%elem(ii) = 1.0_rKind / Lastlam%elem(kk) else Tmpvec%elem(ii) = 0.0_rKind end if kk = kk + Lastlam%dl(1) + 1 end do call contr_diag(Psit%Aa(q), Tmpvec, 3, errst=errst) !if(prop_error('orthogonalize_mps: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:2840', errst=errst)) return !call destroy(Tmpvec) Will be destroyed later, better keep ! Bring into canonical form call canonize_svd(Psit, Psit%ll, 1, Psit%ll) call canonize_svd(Psit, 1, 1, Psit%ll) Psit%can = 'l' ! Calculate maximal left-eigenmatrices V_L of left-orthogonalized unit cell ! ------------------------------------------------------------------------- allocate(xis(min(ncorr + 1, Psit%Aa(2)%dl(3)**2 - 2))) call TransferMatrixWrapper_mps(Psit, xis, VL, 'l', lflag, & lerrcode) if(lerrcode /= 0) write(slog, *) 'error code ', lerrcode, & 'L returned from arpack' maxLev = xis(1) if(lerrcode /= 0) then ndegL = 0 else ndegL = size(VL) if(xis(2) / xis(1) < 0.999999999_rKind) then correlationlengths = -1.0_rKind / log(xis(2) / xis(1)) else correlationlengths = -1.0_rKind end if call create(Evs, [ndegL]) Evs%elem = xis(1:ndegL) end if deallocate(xis) call destroy(Psit) ! Take care of right unit cell ! ============================ ! Form right-canonical unit cell call copy(Psit, Psi) ! Append \Lambda^{-1}_{n-1} to form TI unit cell ! Use pseudoinverse for stability tol = Psit%Aa(1)%dl(1) * maxval(real(Lastlam%elem(:Lastlam%dim))) & * numzero call contr_diag(Psit%Aa(1), Tmpvec, 1, errst=errst) !if(prop_error('orthogonalize_mps: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:2891', errst=errst)) return call destroy(Tmpvec) ! Bring into canonical form call canonize_svd(Psit, 1, 1, Psit%ll) call canonize_svd(Psit, psit%ll, 1, Psit%ll) Psit%can = 'r' ! Calculate maximal right-eigenmatrices V_R of right-orthogonalized unit cell ! --------------------------------------------------------------------------- allocate(xis(min(ncorr + 1, Psit%Aa(2)%dl(3)**2 - 2))) call TransferMatrixWrapper_mps(Psit, xis, VR, 'r', rflag, & rerrcode) if(rerrcode /= 0) write(slog, *) 'error code ', rerrcode, & ' returned from R arpack' maxRev = xis(1) if(lerrcode /= 0) then errcode = lerrcode else errcode = 0 end if if(rerrcode /= 0) then errcode = rerrcode else errcode = 0 end if if((lerrcode /= 0) .and. (rerrcode /= 0)) then return end if if(rerrcode /= 0) then ndegR = 0 else ndegR = size(VR) end if deallocate(xis) call destroy(Psit) ! Next part of the algorithm ! ========================== if(ndegL /= ndegR) then if(lerrcode == 0) then do i = 1, size(VL) call destroy(VL(i)) end do deallocate(VL) call destroy(Evs) end if if(rerrcode == 0) then do i = 1, size(VR) call destroy(VR(i)) end do deallocate(VR) end if tried = tried + 1 if(tried == 10) then errcode = 1000 write(slog, *) 'ndegL and ndegR are not the same after 10 tries' return end if end if end do call destroy(Evs) ndeg = ndegL allocate(Liamok(ndeg), Riamok(ndeg)) Liamok = .false. Riamok = .false. numok = 0 do while(numok == 0) ! 3) Check them for Hermiticity (and invert for positive trace) ! ----------------------------- ! ! * VL(i) hermitian ==> Liamok(i) = true ! * if Tr(VL(i)) < 0 ==> VL(i) = - VL(i) ! * analogue VR do i = 1, ndeg ! left side: VL ! ............. call copy(U, VL(i), scalar=-zone, trans='H', errst=errst) !if(prop_error('orthogonalize_mps: copy '//& ! 'failed.', 'iMPSOps_include.f90:2988', errst=errst)) return call gaxpy(U, 1.0_rKind, VL(i), errst=errst) !if(prop_error('orthogonalize_mps: gaxpy '//& ! 'failed.', 'iMPSOps_include.f90:2992', errst=errst)) return trc = norm(U) if(abs(trc) <= 10.0_rKind * numzero) Liamok(i) = .true. call destroy(U) ! If accepted, fix trace to be positive if(Liamok(i)) then trc = real(trace(VL(i)), KIND=rKind) if(trc < 0.0_rKind) then call scale(-1.0_rKind, VL(i)) end if end if ! right side: VR ! .............. call copy(U, VR(i), scalar=-zone, trans='H', errst=errst) !if(prop_error('orthogonalize_mps: copy '//& ! 'failed.', 'iMPSOps_include.f90:3014', errst=errst)) return call gaxpy(U, 1.0_rKind, VR(i), errst=errst) !if(prop_error('orthogonalize_mps: gaxpy '//& ! 'failed.', 'iMPSOps_include.f90:3018', errst=errst)) return trc = norm(U) if(abs(trc) <= 10.0_rKind * numzero) Riamok(i) = .true. call destroy(U) ! If accepted, fix trace to be positive if(Riamok(i)) then trc = real(trace(VR(i)), KIND=rKind) if(trc < 0.0_rKind) then call scale(-1.0_rKind, VR(i)) end if end if end do ! 4) Check for positive definiteness ! ---------------------------------- ! ! * do i = 1, ndeg ! left side: VL ! ............. if(Liamok(i)) then call copy(U, VL(i)) call create(S, [VL(i)%dl(1)]) call eigd_symm_complex(U%elem, S%elem, VL(i)%dl(1), & errst=errst) !if(prop_error('orthogonalize_mps: eigd_'//& ! 'symm_complex failed.', 'iMPSOps_include.f90:3052', & ! errst=errst)) return ! Are the failed eigenvalues just -epsilon? if(any(S%elem < - 100.0_rKind * numzero)) then write(slog, *) 'it is not ok ...' write(slog, *) 'L failed i', i, S%elem Liamok(i) = .false. else write(slog, *) 'it is ok' end if call destroy(U) call destroy(S) end if ! right side: VR ! .............. if(Riamok(i)) then call copy(U, VR(i)) call create(S, [VR(i)%dl(1)]) call eigd_symm_complex(U%elem, S%elem, VR(i)%dl(1), & errst=errst) !if(prop_error('orthogonalize_mps: eigd_'//& ! 'symm_complex failed.', 'iMPSOps_include.f90:3078', & ! errst=errst)) return if(any(S%elem < - 100.0_rKind * numzero)) then write(slog, *) 'it is not ok...' write(slog, *) 'R failed i', i, S%elem Riamok(i) = .false. else write(slog, *) 'it is ok' end if call destroy(U) call destroy(S) end if ! Count the pairs of hermitian positive matrices if(Liamok(i) .and. Riamok(i)) then numok = numok + 1 else Liamok(i) = .false. Riamok(i) = .false. end if end do ! Some of them are Hermitian and positive definite ! exit the DO-loop with condition (numok == 0) if(numok /= 0) exit ! 5) Forming degenerate matrices into a hermitian and orthonormal set ! ------------------------------------------------------------------- if(alreadytried) then ! Forming was not successful write(slog, *) 'WARNING Orthogonalize_mps: '//& 'no herm. orthnorm. set!' errcode = -400 return else ! Warn the user about the degenerate matrices write(slog, *) 'Orthogonalize_mps: try '//& 'installing herm. orthn. set.' alreadytried = .true. end if ! Form the degenerate matrices into a Hermitian and orthonormal set call stabilize(VL) call stabilize(VR) ! Project onto the well-conditioned subspace call create(Roverlapmat, [ndeg, ndeg]) kk = 1 do j = 1, ndeg do i = 1, ndeg sctmp = real(tracematmul_complex(VL(i)%elem, VR(j)%elem, & VL(i)%dl(1)), KIND=rKind) Roverlapmat%elem(kk) = sctmp kk = kk + 1 end do end do write(slog, *) 'overlaps bf' call write(Roverlapmat, slog, "6") call svd(Ur, S, Vre, Roverlapmat, [1], [2]) write(slog, *) 'singular values of overlap matrix', S%elem allocate(TransXs(S%dl(1)), TransYs(S%dl(1))) do ii = 1, S%dl(1) call create(TransXs(ii), VL(ii)%dl, init='0') call create(TransYs(ii), VR(ii)%dl, init='0') do jj = 1, ndeg kk = jj + (ii - 1) * Ur%dl(1) TransXs(ii)%elem = TransXs(ii)%elem + Ur%elem(kk) * VL(jj)%elem kk = ii + (jj - 1) * Vre%dl(1) TransYs(ii)%elem = TransYs(ii)%elem + Vre%elem(kk) * VR(jj)%elem end do end do do i = 1, S%dl(1) VL(i)%elem = TransXs(i)%elem call destroy(TransXs(i)) VR(i)%elem = TransYs(i)%elem call destroy(TransYs(i)) end do do i = S%dl(1) + 1, ndeg VL(i)%elem = 0.0_rKind VR(i)%elem = 0.0_rKind end do deallocate(TransXs,TransYs) call destroy(Ur) call destroy(S) call destroy(Vre) call destroy(Roverlapmat) end do ! Make the matrices Hermitian and orthonormal in the Frobenius norm. ! ! The overlap-matrix element (ii, jj) is: Tr( VL(ii) * VR(jj)) call create(Roverlapmat, [numok, numok]) lok = 1 do i = 1, ndeg if(.not. Liamok(i)) cycle rok = 1 do j = 1, ndeg if(.not. Riamok(j)) cycle kk = (rok - 1) * numok + lok Roverlapmat%elem(kk) = real(tracematmul_complex(VL(i)%elem, & VR(j)%elem, VR(j)%dl(1)), KIND=rKind) rok = rok + 1 end do lok = lok + 1 end do call svd(Ur, S, Vre, Roverlapmat, [1], [2]) call destroy(Roverlapmat) ! 7) Transform to final basis ! --------------------------- allocate(TransXs(numok), TransYs(numok)) do i = 1, numok call Create(TransXs(i), VL(i)%dl, init='0') call Create(TransYs(i), VR(i)%dl, init='0') lok = 1 do j = 1, ndeg if(.not. Liamok(j)) cycle kk = lok + (i - 1) * Ur%dl(1) TransXs(i)%elem = TransXs(i)%elem + Ur%elem(kk) * VL(j)%elem lok = lok + 1 end do rok = 1 do j = 1, ndeg if(.not. Riamok(j)) cycle kk = i + (rok - 1) * Vre%dl(1) TransYs(i)%elem = TransYs(i)%elem + Vre%elem(kk) * VR(j)%elem rok = rok + 1 end do end do call destroy(Ur) call destroy(Vre) call destroy(S) ! 8) Fix trace ! ------------ do i = 1, numOK trc = real(trace(TransXs(i)), KIND=rKind) if(trc < 0.0_rKind) TransXs(i)%elem = -TransXs(i)%elem trc = real(trace(TransYs(i)), KIND=rKind) if(trc < 0.0_rKind) TransYs(i)%elem = -TransYs(i)%elem end do do i = 1, ndeg call destroy(VL(i)) call destroy(VR(i)) end do deallocate(VL, VR) ! 9) Convert back to original type (real/complex) ! -------------------------------- IF(.true.) THEN ! Real-valued output ! .................. allocate(RealVl(numOk), RealVR(numok)) do i = 1, numOK call copy(U, TransXs(i)) U%elem = aimag(TransXs(i)%elem) trc = norm(U) if(abs(trc) > 10.0_rKind * numzero) then write(slog, *) 'imag part of TransXs(i)', trc errcode = -300 return end if call destroy(U) call create(RealVl(i), TransXs(i)%dl) RealVl(i)%elem = REAL(TransXs(i)%elem, KIND=rKind) call destroy(TransXs(i)) call copy(U, TransYs(i)) U%elem = aimag(TransYs(i)%elem) trc = norm(U) if(abs(trc) > 10.0_rKind * numzero) then write(slog, *) 'imag part of TransYs(i)', trc errcode = -300 return end if call destroy(U) call create(RealVR(i), TransYs(i)%dl) RealVR(i)%elem = real(TransYs(i)%elem, KIND=rKind) call destroy(TransYs(i)) end do else ! Complex-valued output ! ..................... allocate(Realvl(numok), Realvr(numok)) do ii = 1, numok ! Copy VL ! To-Do : Do we need complex Realvl? call create(Realvl(ii), TransXs(ii)%dl) Realvl(ii)%elem = real(TransXs(ii)%elem, KIND=rKind) ! To-Do : Do we need complex Realvr? call create(Realvr(ii), TransYs(ii)%dl) Realvr(ii)%elem = real(TransYs(ii)%elem, KIND=rKind) call destroy(Transxs(i)) call destroy(Transys(i)) end do end if deallocate(TransXs, TransYs) ! 10) Quasi-Cholesky decomposition ! -------------------------------- allocate(Xs(numok), Ys(numOk), LambdaRs(numOK), LambdaRinvs(numok)) do i = 1, numOK ! Quasi-Cholesky decompose the matrices in the proper subspace. ! Decompose this left-eigenmatrix as V_L=X^{\dagger}X ! Using its eigendecomposition rather than Cholesky to avoid difficulties ! near singularity ! To wit, using the spectral decomposition A=Q\Lambda Q^{\dagger} with ! Q the matrix with the eigenvectors of A as columns, X=\sqrt{\Lambda}Q^{\dagger} call create(S, [RealVl(i)%dl(1)]) call eigd_symm_real(RealVl(i)%elem, S%elem, S%dl(1), errst=errst) !if(prop_error('orthogonalize_mps: eigd_'//& ! 'symm_real failed.', 'iMPSOps_include.f90:3339', & ! errst=errst)) return S%elem = sqrt(abs(S%elem)) call copy(Xs(i), RealVl(i), trans='T') call contr_diag(Xs(i), S, 1, errst=errst) !if(prop_error('orthogonalize_mps: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:3347', errst=errst)) return ! Decompose this right-eigenmatrix as V_R=YY^{\dagger} ! Using its eigendecomposition rather than Cholesky to avoid difficulties ! near singularity ! To wit, using the spectral decomposition A=Q\Lambda Q^{\dagger} with ! Q the matrix with the eigenvectors of A as columns, Y=Q\sqrt{\Lambda} call eigd_symm_real(RealVR(i)%elem, S%elem, S%dl(1), errst=errst) !if(prop_error('orthogonalize_mps: eigd_'//& ! 'symm_real failed.', 'iMPSOps_include.f90:3356', & ! errst=errst)) return S%elem = sqrt(abs(S%elem)) call copy(Ys(i), RealVR(i)) call contr_diag(Ys(i), S, 2, errst=errst) !if(prop_error('orthogonalize_mps: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:3364', errst=errst)) return call destroy(RealVL(i)) call destroy(RealVR(i)) call destroy(S) ! Compute ilde{\Lambda_{n-1}}=X\Lambda_{n-1} Y ! and (pseudo-)invert ! To-Do: diagonal matrix - dense contraction is overhead call contr(Rev, Lastlam, Ys(i), [2], [1], errst=errst) !if(prop_error('orthogonalize_mps: contr '//& ! 'failed.', 'iMPSOps_include.f90:3376', errst=errst)) return call contr(LambdaRs(i), Xs(i), Rev, [2], [1], errst=errst) !if(prop_error('orthogonalize_mps: contr '//& ! 'failed.', 'iMPSOps_include.f90:3380', errst=errst)) return call destroy(Rev) ! Pseudoinvert ! (SVD destroys original array, therefore copy) call copy(LambdaRinvs(i), LambdaRs(i)) call svd(U2, S, V2, LambdaRinvs(i), [1], [2]) call destroy(LambdaRinvs(i)) tol = S%dl(1) * maxvalue(S) * numzero do j = 1, S%dl(1) if(S%elem(j) > tol) then S%elem(j) = 1.0_rKind / S%elem(j) else S%elem(j) = 0.0_rKind end if end do call contr_diag(U2, S, 2, errst=errst) !if(prop_error('orthogonalize_mps: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:3404', errst=errst)) return call contr(LambdaRinvs(i), V2, U2, [1], [2], & alpha=done * sqrt(maxlev), errst=errst) !if(prop_error('orthogonalize_mps: contr '//& ! 'failed.', 'iMPSOps_include.f90:3410', errst=errst)) return call destroy(U2) call destroy(V2) call destroy(S) ! To-Do : complex conjugate in contraction? call contr(E, LambdaRs(i), LambdaRs(i), [2], [2], errst=errst) !if(prop_error('orthogonalize_mps: contr '//& ! 'failed.', 'iMPSOps_include.f90:3419', errst=errst)) return ! Normalize the mixed-canonical state trc = real(trace(E), KIND=rKind) call scale(1.0_rKind / sqrt(trc), LambdaRs(i)) call destroy(E) end do deallocate(RealVl, RealVR) end subroutine Orthogonalize_mps
- iMPSOps_f90.orthogonalize_mpsc()[source]¶
fortran-subroutine - ?? () Find the set of Xs(i) and Ys(i) corresponding to the dominant left (right) eigenvectors of the left-canonical (right-canonical) unit cells.
Arguments
- LambdaRsTYPE(matrix)(*), out
??? (normalized)
- LambdaRinvsTYPE(matrix)(*), out
unnormalized pseudo-inverse of LambdaRs
- errcodeINTEGER, out
possibly error code from ARPACK, otherwise 1000: ndegL and ndegR are not the same after 10 tries (-400): no hermitian orthnormormal set (-300): problem in conversion from complex to real
Details
The following steps are performed 1) MISSING DESCRIPTION 2) MISSING DESCRIPTION 3) Mark all hermitian matrices with
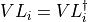 as well
as well
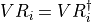 . Assert that these matrices have a
positive trace, so:
. Assert that these matrices have a
positive trace, so:
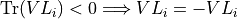 4) Check for all hermitian matrices in an eigenvalue decomposition that
they are positive.
5) Trying to fix situation if there is no pair
4) Check for all hermitian matrices in an eigenvalue decomposition that
they are positive.
5) Trying to fix situation if there is no pair 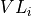 and
and
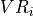 with both hermitian and positive:
with both hermitian and positive:MISSING DESCRIPTION
6) Calculate the overlap matrix of the Frobenius norm
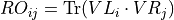 and decompose the
matrix in a SVD
and decompose the
matrix in a SVD 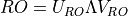 .
TO-DO: THIS IS SYMMETRIC DUE TO TRACE, BUT NOT USED IN CODE (sum possible,
better not replace SVD with eigenvalue until knowing what happens to
negative eigenvalues.
7) Transform to final basis. Assuming all matrices are hermitian positive
the i-th final matrix
.
TO-DO: THIS IS SYMMETRIC DUE TO TRACE, BUT NOT USED IN CODE (sum possible,
better not replace SVD with eigenvalue until knowing what happens to
negative eigenvalues.
7) Transform to final basis. Assuming all matrices are hermitian positive
the i-th final matrix 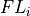 reads like
reads like
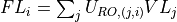 and respectively
and respectively
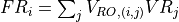 .
8) Assure that all FL, FR have positive trace and assert this if necessary
by multiplying with
.
8) Assure that all FL, FR have positive trace and assert this if necessary
by multiplying with 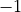 .
9) Convert back to original type, so real or complex. For the real case we
take
.
9) Convert back to original type, so real or complex. For the real case we
take 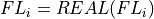 if
if 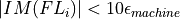 . Analogue for
. Analogue for  .
.MISSING DESCRIPTION FOR COMPLEX (NOT IMPLEMENTED)
10) Quasi-Cholesky decomposition. For the left side we start with the following step: the eigenvalue decomposition is calculate, such that
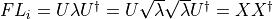 . In general the Cholesky deomposition
would work in this step as well, but in case close to singularity the
eigenvalue decomposition are more stable. The eigenvalue decomposition
on
. In general the Cholesky deomposition
would work in this step as well, but in case close to singularity the
eigenvalue decomposition are more stable. The eigenvalue decomposition
on 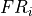 leads to
leads to 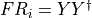 .
Calculate
.
Calculate  . This
matrix is inverted via the pseudo-inverse defined over the SVD. (A
general matrix
. This
matrix is inverted via the pseudo-inverse defined over the SVD. (A
general matrix  has the pseudo-inverse
has the pseudo-inverse
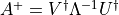 where only
numerical non-zero singular values are considered.)
Finally a normalization is executed
where only
numerical non-zero singular values are considered.)
Finally a normalization is executed 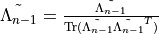 WHY IS PSEUDO-INVERSE NOT NORMALIZED?
WHY IS PSEUDO-INVERSE NOT NORMALIZED?Source Code
show / hide f90 codesubroutine orthogonalize_mpsc(Psi, maxbondd, ndeg, Xs, Ys, LambdaRs, & lambdaRinvs, errcode, lastlam, correlationLengths, errst) TYPE(mpsc) :: psi INTEGER :: maxbondD ! unused integer :: ndeg TYPE(tensorc), INTENT(OUT), POINTER :: Xs(:), Ys(:) TYPE(tensorc), INTENT(OUT), POINTER :: LambdaRs(:), LambdaRinvs(:) INTEGER, INTENT(OUT) :: errcode TYPE(tensorc), INTENT(inout) :: lastlam REAL(KIND=rKind), INTENT(OUT) :: correlationLengths(:) integer, intent(out), optional :: errst ! Local variables ! --------------- ! record try for forming a hermitian orthonormal set from the ! degenerate matrices logical :: alreadytried = .false. ! for looping integer :: ii, jj, i, j ! for indexing integer :: kk ! looping/counter for the hermitian positive matrices integer :: lok, rok ! number of tensors in the MPS integer :: q ! number of hermitian and positive pairs of matrices in VL, VR integer :: numok ! check if matrices have positive trace (only local use inside loop) ! Also abused as norm real(KIND=rKind) :: trc ! i-th entry indicates if VL(i) is hermitian and positive (respectively VR(i)) ! .false. is as well set if other R/Liamok is not hermitian positive logical, allocatable :: Liamok(:), Riamok(:) ! logical :: lflag, rflag integer :: ncorr, ndegL, ndegR, lerrcode, rerrcode, k, chi, tried ! temporary scalar real(KIND=rKind) :: sctmp ! working copy of the MPS type(mpsc) :: psit ! Singular values for all SVDs type(tensor) :: S ! Temporary vector type(tensorc) :: Tmpvec ! Unitary matrices for the SVD of the eigenmatrix (always complex) type(tensorc) :: U, V ! Unitary matrices for the SVD of the (real-valued) overlap matrix type(tensor) :: Ur, Vre ! Unitary matrix for remaining type-dependent SVD at the end type(tensorc) :: U2, V2 type(tensor), POINTER :: RealVl(:), RealVr(:) type(tensorc), POINTER :: VL(:), VR(:), TransXs(:), TransYs(:) type(tensor) :: roverlapmat ! Temporary tensor type(tensorc) :: Rev ! Mixed-canonical state type(tensorc) :: E type(tensor) :: evs type(tensor) :: Atmp real(KIND=rKind) :: maxLev, subLev, maxRev, tol, zip, nrm1,nrm2 integer, allocatable :: indx(:) real(KIND=rKind), allocatable :: xis(:), eigw(:), tmp(:) type(tensor), pointer :: VLR(:) !if(present(errst)) errst = 0 q = Psi%ll ! \chi=1 states cause issues, but we know exactly what everything is... if(Psi%Aa(q)%dl(3) == 1) then write(slog, *) 'chi=1 used!' errcode = 0 ndeg = 1 allocate(Xs(ndeg), Ys(ndeg), LambdaRs(ndeg), LambdaRinvs(ndeg)) call create(Xs(1), [1, 1], init='1') call create(Ys(1), [1, 1], init='1') call create(LambdaRs(1), [1, 1], init='1') call create(LambdaRinvs(1), [1, 1], init='1') correlationlengths = 0.0_rKind return end if ncorr = 20 ndegL = 0 ndegR = 1 tried = 0 do while(ndegL .ne. ndegR) ! Take care of left unit cell ! =========================== ! Form left-canonical unit cell call copy(Psit, Psi) ! Append \Lambda^{-1}_{n-1} to form TI unit cell ! Use pseudoinverse for stability tol = Psit%Aa(q)%dl(3) * maxval(real(Lastlam%elem(:Lastlam%dim))) & * numzero call create(Tmpvec, [Lastlam%dl(1)]) kk = 1 do ii = 1, Lastlam%dl(1) if(real(Lastlam%elem(kk)) > tol) then Tmpvec%elem(ii) = 1.0_rKind / Lastlam%elem(kk) else Tmpvec%elem(ii) = 0.0_rKind end if kk = kk + Lastlam%dl(1) + 1 end do call contr_diag(Psit%Aa(q), Tmpvec, 3, errst=errst) !if(prop_error('orthogonalize_mpsc: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:2840', errst=errst)) return !call destroy(Tmpvec) Will be destroyed later, better keep ! Bring into canonical form call canonize_svd(Psit, Psit%ll, 1, Psit%ll) call canonize_svd(Psit, 1, 1, Psit%ll) Psit%can = 'l' ! Calculate maximal left-eigenmatrices V_L of left-orthogonalized unit cell ! ------------------------------------------------------------------------- allocate(xis(min(ncorr + 1, Psit%Aa(2)%dl(3)**2 - 2))) call TransferMatrixWrapper_mpsc(Psit, xis, VL, 'l', lflag, & lerrcode) if(lerrcode /= 0) write(slog, *) 'error code ', lerrcode, & 'L returned from arpack' maxLev = xis(1) if(lerrcode /= 0) then ndegL = 0 else ndegL = size(VL) if(xis(2) / xis(1) < 0.999999999_rKind) then correlationlengths = -1.0_rKind / log(xis(2) / xis(1)) else correlationlengths = -1.0_rKind end if call create(Evs, [ndegL]) Evs%elem = xis(1:ndegL) end if deallocate(xis) call destroy(Psit) ! Take care of right unit cell ! ============================ ! Form right-canonical unit cell call copy(Psit, Psi) ! Append \Lambda^{-1}_{n-1} to form TI unit cell ! Use pseudoinverse for stability tol = Psit%Aa(1)%dl(1) * maxval(real(Lastlam%elem(:Lastlam%dim))) & * numzero call contr_diag(Psit%Aa(1), Tmpvec, 1, errst=errst) !if(prop_error('orthogonalize_mpsc: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:2891', errst=errst)) return call destroy(Tmpvec) ! Bring into canonical form call canonize_svd(Psit, 1, 1, Psit%ll) call canonize_svd(Psit, psit%ll, 1, Psit%ll) Psit%can = 'r' ! Calculate maximal right-eigenmatrices V_R of right-orthogonalized unit cell ! --------------------------------------------------------------------------- allocate(xis(min(ncorr + 1, Psit%Aa(2)%dl(3)**2 - 2))) call TransferMatrixWrapper_mpsc(Psit, xis, VR, 'r', rflag, & rerrcode) if(rerrcode /= 0) write(slog, *) 'error code ', rerrcode, & ' returned from R arpack' maxRev = xis(1) if(lerrcode /= 0) then errcode = lerrcode else errcode = 0 end if if(rerrcode /= 0) then errcode = rerrcode else errcode = 0 end if if((lerrcode /= 0) .and. (rerrcode /= 0)) then return end if if(rerrcode /= 0) then ndegR = 0 else ndegR = size(VR) end if deallocate(xis) call destroy(Psit) ! Next part of the algorithm ! ========================== if(ndegL /= ndegR) then if(lerrcode == 0) then do i = 1, size(VL) call destroy(VL(i)) end do deallocate(VL) call destroy(Evs) end if if(rerrcode == 0) then do i = 1, size(VR) call destroy(VR(i)) end do deallocate(VR) end if tried = tried + 1 if(tried == 10) then errcode = 1000 write(slog, *) 'ndegL and ndegR are not the same after 10 tries' return end if end if end do call destroy(Evs) ndeg = ndegL allocate(Liamok(ndeg), Riamok(ndeg)) Liamok = .false. Riamok = .false. numok = 0 do while(numok == 0) ! 3) Check them for Hermiticity (and invert for positive trace) ! ----------------------------- ! ! * VL(i) hermitian ==> Liamok(i) = true ! * if Tr(VL(i)) < 0 ==> VL(i) = - VL(i) ! * analogue VR do i = 1, ndeg ! left side: VL ! ............. call copy(U, VL(i), scalar=-zone, trans='H', errst=errst) !if(prop_error('orthogonalize_mpsc: copy '//& ! 'failed.', 'iMPSOps_include.f90:2988', errst=errst)) return call gaxpy(U, 1.0_rKind, VL(i), errst=errst) !if(prop_error('orthogonalize_mpsc: gaxpy '//& ! 'failed.', 'iMPSOps_include.f90:2992', errst=errst)) return trc = norm(U) if(abs(trc) <= 10.0_rKind * numzero) Liamok(i) = .true. call destroy(U) ! If accepted, fix trace to be positive if(Liamok(i)) then trc = real(trace(VL(i)), KIND=rKind) if(trc < 0.0_rKind) then call scale(-1.0_rKind, VL(i)) end if end if ! right side: VR ! .............. call copy(U, VR(i), scalar=-zone, trans='H', errst=errst) !if(prop_error('orthogonalize_mpsc: copy '//& ! 'failed.', 'iMPSOps_include.f90:3014', errst=errst)) return call gaxpy(U, 1.0_rKind, VR(i), errst=errst) !if(prop_error('orthogonalize_mpsc: gaxpy '//& ! 'failed.', 'iMPSOps_include.f90:3018', errst=errst)) return trc = norm(U) if(abs(trc) <= 10.0_rKind * numzero) Riamok(i) = .true. call destroy(U) ! If accepted, fix trace to be positive if(Riamok(i)) then trc = real(trace(VR(i)), KIND=rKind) if(trc < 0.0_rKind) then call scale(-1.0_rKind, VR(i)) end if end if end do ! 4) Check for positive definiteness ! ---------------------------------- ! ! * do i = 1, ndeg ! left side: VL ! ............. if(Liamok(i)) then call copy(U, VL(i)) call create(S, [VL(i)%dl(1)]) call eigd_symm_complex(U%elem, S%elem, VL(i)%dl(1), & errst=errst) !if(prop_error('orthogonalize_mpsc: eigd_'//& ! 'symm_complex failed.', 'iMPSOps_include.f90:3052', & ! errst=errst)) return ! Are the failed eigenvalues just -epsilon? if(any(S%elem < - 100.0_rKind * numzero)) then write(slog, *) 'it is not ok ...' write(slog, *) 'L failed i', i, S%elem Liamok(i) = .false. else write(slog, *) 'it is ok' end if call destroy(U) call destroy(S) end if ! right side: VR ! .............. if(Riamok(i)) then call copy(U, VR(i)) call create(S, [VR(i)%dl(1)]) call eigd_symm_complex(U%elem, S%elem, VR(i)%dl(1), & errst=errst) !if(prop_error('orthogonalize_mpsc: eigd_'//& ! 'symm_complex failed.', 'iMPSOps_include.f90:3078', & ! errst=errst)) return if(any(S%elem < - 100.0_rKind * numzero)) then write(slog, *) 'it is not ok...' write(slog, *) 'R failed i', i, S%elem Riamok(i) = .false. else write(slog, *) 'it is ok' end if call destroy(U) call destroy(S) end if ! Count the pairs of hermitian positive matrices if(Liamok(i) .and. Riamok(i)) then numok = numok + 1 else Liamok(i) = .false. Riamok(i) = .false. end if end do ! Some of them are Hermitian and positive definite ! exit the DO-loop with condition (numok == 0) if(numok /= 0) exit ! 5) Forming degenerate matrices into a hermitian and orthonormal set ! ------------------------------------------------------------------- if(alreadytried) then ! Forming was not successful write(slog, *) 'WARNING Orthogonalize_mpsc: '//& 'no herm. orthnorm. set!' errcode = -400 return else ! Warn the user about the degenerate matrices write(slog, *) 'Orthogonalize_mpsc: try '//& 'installing herm. orthn. set.' alreadytried = .true. end if ! Form the degenerate matrices into a Hermitian and orthonormal set call stabilize(VL) call stabilize(VR) ! Project onto the well-conditioned subspace call create(Roverlapmat, [ndeg, ndeg]) kk = 1 do j = 1, ndeg do i = 1, ndeg sctmp = real(tracematmul_complex(VL(i)%elem, VR(j)%elem, & VL(i)%dl(1)), KIND=rKind) Roverlapmat%elem(kk) = sctmp kk = kk + 1 end do end do write(slog, *) 'overlaps bf' call write(Roverlapmat, slog, "6") call svd(Ur, S, Vre, Roverlapmat, [1], [2]) write(slog, *) 'singular values of overlap matrix', S%elem allocate(TransXs(S%dl(1)), TransYs(S%dl(1))) do ii = 1, S%dl(1) call create(TransXs(ii), VL(ii)%dl, init='0') call create(TransYs(ii), VR(ii)%dl, init='0') do jj = 1, ndeg kk = jj + (ii - 1) * Ur%dl(1) TransXs(ii)%elem = TransXs(ii)%elem + Ur%elem(kk) * VL(jj)%elem kk = ii + (jj - 1) * Vre%dl(1) TransYs(ii)%elem = TransYs(ii)%elem + Vre%elem(kk) * VR(jj)%elem end do end do do i = 1, S%dl(1) VL(i)%elem = TransXs(i)%elem call destroy(TransXs(i)) VR(i)%elem = TransYs(i)%elem call destroy(TransYs(i)) end do do i = S%dl(1) + 1, ndeg VL(i)%elem = 0.0_rKind VR(i)%elem = 0.0_rKind end do deallocate(TransXs,TransYs) call destroy(Ur) call destroy(S) call destroy(Vre) call destroy(Roverlapmat) end do ! Make the matrices Hermitian and orthonormal in the Frobenius norm. ! ! The overlap-matrix element (ii, jj) is: Tr( VL(ii) * VR(jj)) call create(Roverlapmat, [numok, numok]) lok = 1 do i = 1, ndeg if(.not. Liamok(i)) cycle rok = 1 do j = 1, ndeg if(.not. Riamok(j)) cycle kk = (rok - 1) * numok + lok Roverlapmat%elem(kk) = real(tracematmul_complex(VL(i)%elem, & VR(j)%elem, VR(j)%dl(1)), KIND=rKind) rok = rok + 1 end do lok = lok + 1 end do call svd(Ur, S, Vre, Roverlapmat, [1], [2]) call destroy(Roverlapmat) ! 7) Transform to final basis ! --------------------------- allocate(TransXs(numok), TransYs(numok)) do i = 1, numok call Create(TransXs(i), VL(i)%dl, init='0') call Create(TransYs(i), VR(i)%dl, init='0') lok = 1 do j = 1, ndeg if(.not. Liamok(j)) cycle kk = lok + (i - 1) * Ur%dl(1) TransXs(i)%elem = TransXs(i)%elem + Ur%elem(kk) * VL(j)%elem lok = lok + 1 end do rok = 1 do j = 1, ndeg if(.not. Riamok(j)) cycle kk = i + (rok - 1) * Vre%dl(1) TransYs(i)%elem = TransYs(i)%elem + Vre%elem(kk) * VR(j)%elem rok = rok + 1 end do end do call destroy(Ur) call destroy(Vre) call destroy(S) ! 8) Fix trace ! ------------ do i = 1, numOK trc = real(trace(TransXs(i)), KIND=rKind) if(trc < 0.0_rKind) TransXs(i)%elem = -TransXs(i)%elem trc = real(trace(TransYs(i)), KIND=rKind) if(trc < 0.0_rKind) TransYs(i)%elem = -TransYs(i)%elem end do do i = 1, ndeg call destroy(VL(i)) call destroy(VR(i)) end do deallocate(VL, VR) ! 9) Convert back to original type (real/complex) ! -------------------------------- IF(.false.) THEN ! Real-valued output ! .................. allocate(RealVl(numOk), RealVR(numok)) do i = 1, numOK call copy(U, TransXs(i)) U%elem = aimag(TransXs(i)%elem) trc = norm(U) if(abs(trc) > 10.0_rKind * numzero) then write(slog, *) 'imag part of TransXs(i)', trc errcode = -300 return end if call destroy(U) call create(RealVl(i), TransXs(i)%dl) RealVl(i)%elem = REAL(TransXs(i)%elem, KIND=rKind) call destroy(TransXs(i)) call copy(U, TransYs(i)) U%elem = aimag(TransYs(i)%elem) trc = norm(U) if(abs(trc) > 10.0_rKind * numzero) then write(slog, *) 'imag part of TransYs(i)', trc errcode = -300 return end if call destroy(U) call create(RealVR(i), TransYs(i)%dl) RealVR(i)%elem = real(TransYs(i)%elem, KIND=rKind) call destroy(TransYs(i)) end do else ! Complex-valued output ! ..................... allocate(Realvl(numok), Realvr(numok)) do ii = 1, numok ! Copy VL ! To-Do : Do we need complex Realvl? call create(Realvl(ii), TransXs(ii)%dl) Realvl(ii)%elem = real(TransXs(ii)%elem, KIND=rKind) ! To-Do : Do we need complex Realvr? call create(Realvr(ii), TransYs(ii)%dl) Realvr(ii)%elem = real(TransYs(ii)%elem, KIND=rKind) call destroy(Transxs(i)) call destroy(Transys(i)) end do end if deallocate(TransXs, TransYs) ! 10) Quasi-Cholesky decomposition ! -------------------------------- allocate(Xs(numok), Ys(numOk), LambdaRs(numOK), LambdaRinvs(numok)) do i = 1, numOK ! Quasi-Cholesky decompose the matrices in the proper subspace. ! Decompose this left-eigenmatrix as V_L=X^{\dagger}X ! Using its eigendecomposition rather than Cholesky to avoid difficulties ! near singularity ! To wit, using the spectral decomposition A=Q\Lambda Q^{\dagger} with ! Q the matrix with the eigenvectors of A as columns, X=\sqrt{\Lambda}Q^{\dagger} call create(S, [RealVl(i)%dl(1)]) call eigd_symm_real(RealVl(i)%elem, S%elem, S%dl(1), errst=errst) !if(prop_error('orthogonalize_mpsc: eigd_'//& ! 'symm_real failed.', 'iMPSOps_include.f90:3339', & ! errst=errst)) return S%elem = sqrt(abs(S%elem)) call copy(Xs(i), RealVl(i), trans='T') call contr_diag(Xs(i), S, 1, errst=errst) !if(prop_error('orthogonalize_mpsc: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:3347', errst=errst)) return ! Decompose this right-eigenmatrix as V_R=YY^{\dagger} ! Using its eigendecomposition rather than Cholesky to avoid difficulties ! near singularity ! To wit, using the spectral decomposition A=Q\Lambda Q^{\dagger} with ! Q the matrix with the eigenvectors of A as columns, Y=Q\sqrt{\Lambda} call eigd_symm_real(RealVR(i)%elem, S%elem, S%dl(1), errst=errst) !if(prop_error('orthogonalize_mpsc: eigd_'//& ! 'symm_real failed.', 'iMPSOps_include.f90:3356', & ! errst=errst)) return S%elem = sqrt(abs(S%elem)) call copy(Ys(i), RealVR(i)) call contr_diag(Ys(i), S, 2, errst=errst) !if(prop_error('orthogonalize_mpsc: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:3364', errst=errst)) return call destroy(RealVL(i)) call destroy(RealVR(i)) call destroy(S) ! Compute ilde{\Lambda_{n-1}}=X\Lambda_{n-1} Y ! and (pseudo-)invert ! To-Do: diagonal matrix - dense contraction is overhead call contr(Rev, Lastlam, Ys(i), [2], [1], errst=errst) !if(prop_error('orthogonalize_mpsc: contr '//& ! 'failed.', 'iMPSOps_include.f90:3376', errst=errst)) return call contr(LambdaRs(i), Xs(i), Rev, [2], [1], errst=errst) !if(prop_error('orthogonalize_mpsc: contr '//& ! 'failed.', 'iMPSOps_include.f90:3380', errst=errst)) return call destroy(Rev) ! Pseudoinvert ! (SVD destroys original array, therefore copy) call copy(LambdaRinvs(i), LambdaRs(i)) call svd(U2, S, V2, LambdaRinvs(i), [1], [2]) call destroy(LambdaRinvs(i)) tol = S%dl(1) * maxvalue(S) * numzero do j = 1, S%dl(1) if(S%elem(j) > tol) then S%elem(j) = 1.0_rKind / S%elem(j) else S%elem(j) = 0.0_rKind end if end do call contr_diag(U2, S, 2, errst=errst) !if(prop_error('orthogonalize_mpsc: contr_diag '//& ! 'failed.', 'iMPSOps_include.f90:3404', errst=errst)) return call contr(LambdaRinvs(i), V2, U2, [1], [2], & alpha=zone * sqrt(maxlev), errst=errst) !if(prop_error('orthogonalize_mpsc: contr '//& ! 'failed.', 'iMPSOps_include.f90:3410', errst=errst)) return call destroy(U2) call destroy(V2) call destroy(S) ! To-Do : complex conjugate in contraction? call contr(E, LambdaRs(i), LambdaRs(i), [2], [2], errst=errst) !if(prop_error('orthogonalize_mpsc: contr '//& ! 'failed.', 'iMPSOps_include.f90:3419', errst=errst)) return ! Normalize the mixed-canonical state trc = real(trace(E), KIND=rKind) call scale(1.0_rKind / sqrt(trc), LambdaRs(i)) call destroy(E) end do deallocate(RealVl, RealVR) end subroutine Orthogonalize_mpsc
- iMPSOps_f90.observe_infinite_mps()[source]¶
fortran-subroutine - June 2018 (dj, updated) Measurements on an infinite MPS
Arguments
- errcodeINTEGER, in
error flag from preceeding subroutines. If not equal to zero dummy results are written.
Source Code
show / hide f90 codesubroutine observe_infinite_mps(Psit, ndeg, LambdaRs, Operators, & MyObs, obsname, obsunit, energy, of, converged, Imapper, & Cp, errcode, err, oftol, errst) type(mps), dimension(:), pointer, intent(inout) :: Psit integer, intent(in) :: ndeg type(tensor), dimension(:), pointer :: LambdaRs type(tensorlist), intent(inout) :: Operators type(obs_r), intent(inout) :: MyObs character(len=*), intent(in) :: obsname integer, intent(in) :: obsunit real(KIND=rKind), intent(in) :: energy, of logical, intent(in) :: converged type(imap), intent(in) :: Imapper type(ConvParam), intent(in) :: Cp integer, intent(in) :: errcode real(KIND=rKind), intent(in) :: err, oftol integer, intent(out), optional :: errst ! Local variables ! --------------- ! for looping integer :: ii, jj, kk, pp ! index in array integer :: idx ! next index in terms of unit cell integer :: next ! bond dimension integer :: bd ! number of sites in unit cell (short-cut) integer :: qq ! Correlation results (corr, fermi-corr, string-corr) real(KIND=rKind) :: sc real(KIND=rKind), dimension(:, :), allocatable :: corr, fcorr, & scorr ! Format strings for write(*, *) character(16) :: iwstring, specstring ! Reduced density matrix type(tensor) :: Rho type(tensorlist) :: Rhos ! Tensor for singular values type(tensor) :: Tlam ! Singular values type(tensor) :: Lambda ! temporary tensors type(tensor) :: Tmp, Tmpb, Tmpc ! Left transfer matrix for correlation measures type(tensor) :: Ltheta ! Temporary operators type(tensor) :: Tmpo ! Copy of MPS unit cell for mixed-canonical unit cell type(mps) :: Phi !if(present(errst)) errst = 0 qq = Psit(1)%ll bd = maxchi(Psit(1)) open(unit=obsunit, file=trim(obsname), status='replace', action='write') ! Write out correlation lengths - header of results write(obsunit, '(1I16)') errcode if(errcode /= 0) then close(obsunit) return end if write(obsunit, '(1I16)') ndeg write(obsunit, '(1I16)') size(Psit,1) write(obsunit, '(1I16)') bd write(obsunit, '(1E30.15)') MyObs%CorrelationLengths(1) write(obsunit, '(3E30.15)') of, err, oftol write(obsunit, '(1E30.15)') energy / (qq * 1.0_rKind) ! Allocate memory for correlators if(MyObs%CO%ncorr > 0) then allocate(corr(MyObs%CO%ncorr, 0:MyObs%corr_range)) end if if(MyObs%FCO%ncorr > 0) then allocate(fcorr(MyObs%FCO%ncorr, 0:MyObs%corr_range)) end if if(MyObs%STO%nstring > 0) then allocate(scorr(MyObs%STO%nstring, 0:MyObs%corr_range)) end if do pp = 1, size(Psit, 1) ! Generate mixed-canonical unit cell in Phi call copy(Phi, Psit(pp)) call contr(Tmp, Phi%Aa(qq), LambdaRs(pp), [3], [1], errst=errst) !if(prop_error('observe_infinite_mps : contr failed.', & ! 'iMPSOps_include.f90:3570', errst=errst)) return call destroy(Phi%Aa(qq)) call copy(Phi%Aa(qq), Tmp) if(MyObs%BE%bondentr) then ! Bond entropy - data point to the right ! ............ call svd(Tmpb, Tlam, Tmpc, Tmp, [1, 2], [3], errst=errst) !if(prop_error('observe_infinite_mps : svd '//& ! 'failed.', 'iMPSOps_include.f90:3581', errst=errst)) return call destroy(Tmpb) call destroy(Tmpc) call destroy(Tmp) Phi%haslambda(qq + 1) = .true. call copy(Phi%Lambda(qq + 1), Tlam) call lambdas_to_vec(Lambda, Tlam) call destroy(Tlam) Lambda%elem = Lambda%elem**2 do jj = 1, Lambda%dl(1) if(Lambda%elem(jj) > numzero) then MyObs%BE%elem(qq + 1) = MyObs%BE%elem(qq + 1) & - Lambda%elem(jj) & * log(Lambda%elem(jj)) end if end do call destroy(Lambda) else call destroy(Tmp) end if Phi%can(qq) = 'c' Phi%oc = qq ! Allocate list to store reduced density matrices call create(Rhos, qq) ! Reset correlation results (they are added to exising array) if(MyObs%CO%ncorr > 0) corr = 0.0_rKind if(MyObs%FCO%ncorr > 0) fcorr = 0.0_rKind if(MyObs%STO%nstring > 0) scorr = 0.0_rKind sites: do ii = qq, 1, (-1) if(ii /= Phi%oc) call canonize_svd(Phi, ii) if((ii < qq) .and. MyObs%BE%bondentr) then ! Bond entropy - data points in the bulk ! ............ call lambdas_to_vec(Lambda, Phi%Lambda(ii + 1)) Lambda%elem = Lambda%elem**2 do jj = 1, Lambda%dl(1) if(Lambda%elem(jj) > numzero) then MyObs%BE%elem(ii + 1) = MyObs%BE%elem(ii + 1) & - Lambda%elem(jj) & * log(Lambda%elem(jj)) end if end do call destroy(Lambda) end if call rho_kk(Rho, Phi, ii, errst=errst) !if(prop_error('observe_infinite_mps : rho_kk '//& ! 'failed.', 'iMPSOps_include.f90:3643', errst=errst)) return call copy(Rhos%Li(ii), Rho) if(MyObs%Ri%hasrho_i) then ! Single site density matrices ! ............................ idx = findtagindex(ii, MyObs%Ri%rho_i_i) if(idx > 0) call qmattomat(MyObs%Ri%Elem(ii), Rho, Imapper) end if ! Single-site observables ! ....................... local: do jj = 1, MyObs%SO%nsite MyObs%SO%elem(ii, jj) = MyObs%SO%Si(jj)%w & * real(trace_rho_x_mat(Rho, & Operators%Li(MyObs%SO%Si(jj)%o))) end do local ! Correlators (two-site) ! ...................... do jj = 1, MyObs%CO%ncorr idx = MyObs%CO%corrid(jj) ! Diagonal element call contr(Tmpo, Operators%Li(MyObs%CO%Corr(jj)%ol), & Operators%Li(MyObs%CO%Corr(jj)%or), [2], [1], & errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'contr failed.', 'iMPSOps_include.f90:3676', & ! errst=errst)) return call set_hash(Tmpo, [2], errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'set_hash failed.', 'iMPSOps_include.f90:3681', & ! errst=errst)) return corr(idx, 0) = corr(idx, 0) & + trace_rho_x_mat(Rhos%Li(ii), Tmpo) & * MyObs%CO%Corr(jj)%w call destroy(Tmpo) ! Propagate through the tensor network ! . . . . . . . . . . . . . . . . . . call copy(Tmp, Phi%Aa(ii)) call corr_init_l_mps(Tmp, Ltheta, & Operators%Li(MyObs%CO%Corr(jj)%or)) call destroy(Tmp) next = ii do kk = 1, MyObs%corr_range next = next - 1 if(next == 0) next = qq call corr_meas_l_mps(sc, Psit(pp)%Aa(next), & MyObs%corr_range + 1 - kk, Ltheta, & Operators%Li(MyObs%CO%Corr(jj)%ol), & Operators%Li(1), .false., errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:3709', & ! errst=errst)) return corr(idx, kk) = corr(idx, kk) & + sc * MyObs%CO%Corr(jj)%w end do end do ! Fermi correlation functions ! ........................... do jj = 1, MyObs%FCO%ncorr idx = MyObs%FCO%corrid(jj) ! Diagonal element call contr(Tmpo, Operators%Li(MyObs%FCO%Corr(jj)%ol), & Operators%Li(MyObs%FCO%Corr(jj)%or), [2], [1], & errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'contr failed.', 'iMPSOps_include.f90:3728', & ! errst=errst)) return call set_hash(Tmpo, [2], errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'set_hash failed.', 'iMPSOps_include.f90:3733', & ! errst=errst)) return fcorr(idx, 0) = fcorr(idx, 0) & + trace_rho_x_mat(Rhos%Li(ii), Tmpo) & * MyObs%FCO%Corr(jj)%w call destroy(Tmpo) ! Propagate through the tensor network ! . . . . . . . . . . . . . . . . . . call copy(Tmp, Phi%Aa(ii)) call corr_init_l_mps(Tmp, Ltheta, & Operators%Li(MyObs%FCO%Corr(jj)%or)) call destroy(Tmp) next = ii do kk = 1, MyObs%corr_range next = next - 1 if(next == 0) next = qq call corr_meas_l_mps(sc, Psit(pp)%Aa(next), & MyObs%corr_range + 1 - kk, Ltheta, & Operators%Li(MyObs%FCO%Corr(jj)%ol), & Operators%Li(MyObs%FCO%fop), .true., errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'corr_meas failed.', 'iMPSOps_include.f90:3761', & ! errst=errst)) return fcorr(idx, kk) = fcorr(idx, kk) & + sc * MyObs%FCO%Corr(jj)%w end do end do ! String correlator functions ! ........................... do jj = 1, MyObs%STO%nstring ! Diagonal element call contr(Tmpo, Operators%Li(MyObs%STO%String(jj)%ol), & Operators%Li(MyObs%STO%String(jj)%or), & [2], [1], errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'contr failed.', 'iMPSOps_include.f90:3778', & ! errst=errst)) return call set_hash(Tmpo, [2], errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'set_hash failed.', 'iMPSOps_include.f90:3783', & ! errst=errst)) return scorr(idx, 0) = scorr(idx, 0) & + trace_rho_x_mat(Rhos%Li(ii), Tmpo) & * MyObs%STO%String(jj)%w call destroy(Tmpo) ! Propagate through the tensor network ! . . . . . . . . . . . . . . . . . . call copy(Tmp, Phi%Aa(ii)) call corr_init_l_mps(Tmp, Ltheta, & Operators%Li(MyObs%STO%String(jj)%or)) call destroy(Tmp) next = ii do kk = 1, MyObs%corr_range next = next - 1 if(next == 0) next = qq call corr_meas_l_mps(sc, Psit(pp)%Aa(next), & MyObs%corr_range + 1 - kk, Ltheta, & Operators%Li(MyObs%STO%String(jj)%ol), & Operators%Li(MyObs%STO%String(jj)%od), .true., & errst=errst) !if(prop_error('observe_infinite_mps : '//& ! 'corr_meas failed.', 'iMPSOps_include.f90:3812', & ! errst=errst)) return scorr(idx, kk) = scorr(idx, kk) & + sc * MyObs%STO%String(jj)%w end do end do ! Entropy single site (density matrix replaced with eigenvectors) ! ................... if(MyObs%SE%siteentr) then call entropy_rho_kk(MyObs%SE%elem(ii), Rho, errst=errst) end if call destroy(Rho) end do sites if(MyObs%BE%bondentr) then ! Bond entropy - data point to the left ! ............ call svd(Tmpb, Tlam, Tmpc, Phi%Aa(1), [1], [2, 3], errst=errst) !if(prop_error('observe_infinite_mps : svd '//& ! 'failed.', 'iMPSOps_include.f90:3837', errst=errst)) return call destroy(Tmpb) call destroy(Tmpc) call lambdas_to_vec(Lambda, Tlam) call destroy(Tlam) Lambda%elem = Lambda%elem**2 do jj = 1, Lambda%dl(1) if(Lambda%elem(jj) > numzero) then MyObs%BE%elem(1) = MyObs%BE%elem(1) & - Lambda%elem(jj) & * log(Lambda%elem(jj)) end if end do call destroy(Lambda) end if ! Deallocate list of all reduced single-site density matrices call destroy(Rhos) call destroy(Phi) ! Have to write all those results by hand ! --------------------------------------- ! Divide correlations by length of unit cell if(MyObs%CO%ncorr > 0) corr = corr / real(qq, KIND=rKind) if(MyObs%FCO%ncorr > 0) fcorr = fcorr / real(qq, KIND=rKind) if(MyObs%STO%nstring > 0) scorr = scorr / real(qq, KIND=rKind) ! Default string specifier for size of unit cell write(iwstring, '(I4)') qq specstring = "("//trim(adjustl(iwstring))//"E30.15E3)" call write(MyObs%SO, obsunit, specstring) call write(MyObs%SE, obsunit, specstring) call write(MyObs%BE, obsunit) ! Default string specifier for corr_range write(iwstring, '(I4)') MyObs%corr_range + 1 specstring = "("//trim(adjustl(iwstring))//"E30.15E3)" do jj = 1, MyObs%CO%ncorr if(MyObs%CO%isherm(jj)) then write(obsunit, '(1A1)') 'R' else write(obsunit, '(1A1)') 'R' end if write(obsunit, specstring) real(corr(jj, :), KIND=rKind) !if(.not. MyObs%CO%isherm(jj)) then ! write(obsunit, specstring) aimag(corr(jj, :)) !end if end do do jj = 1, MyObs%FCO%ncorr if(MyObs%FCO%isherm(jj)) then write(obsunit, '(1A1)') 'R' else write(obsunit, '(1A1)') 'R' end if write(obsunit, specstring) real(fcorr(jj, :), KIND=rKind) !if(.not. MyObs%FCO%isherm(jj)) then ! write(obsunit, specstring) aimag(fcorr(jj, :)) !end if end do do jj = 1, MyObs%STO%nstring write(obsunit, specstring) real(scorr(jj, :), KIND=rKind) end do end do ! Deallocate space for correlation measurements if(MyObs%CO%ncorr > 0) deallocate(corr) if(MyObs%FCO%ncorr > 0) deallocate(fcorr) if(MyObs%STO%nstring > 0) deallocate(scorr) close(obsunit) end subroutine observe_infinite_mps
- iMPSOps_f90.observe_infinite_mpsc()[source]¶
fortran-subroutine - June 2018 (dj, updated) Measurements on an infinite MPS
Arguments
- errcodeINTEGER, in
error flag from preceeding subroutines. If not equal to zero dummy results are written.
Source Code
show / hide f90 codesubroutine observe_infinite_mpsc(Psit, ndeg, LambdaRs, Operators, & MyObs, obsname, obsunit, energy, of, converged, Imapper, & Cp, errcode, err, oftol, errst) type(mpsc), dimension(:), pointer, intent(inout) :: Psit integer, intent(in) :: ndeg type(tensorc), dimension(:), pointer :: LambdaRs type(tensorlistc), intent(inout) :: Operators type(obsc), intent(inout) :: MyObs character(len=*), intent(in) :: obsname integer, intent(in) :: obsunit real(KIND=rKind), intent(in) :: energy, of logical, intent(in) :: converged type(imap), intent(in) :: Imapper type(ConvParam), intent(in) :: Cp integer, intent(in) :: errcode real(KIND=rKind), intent(in) :: err, oftol integer, intent(out), optional :: errst ! Local variables ! --------------- ! for looping integer :: ii, jj, kk, pp ! index in array integer :: idx ! next index in terms of unit cell integer :: next ! bond dimension integer :: bd ! number of sites in unit cell (short-cut) integer :: qq ! Correlation results (corr, fermi-corr, string-corr) complex(KIND=rKind) :: sc complex(KIND=rKind), dimension(:, :), allocatable :: corr, fcorr, & scorr ! Format strings for write(*, *) character(16) :: iwstring, specstring ! Reduced density matrix type(tensorc) :: Rho type(tensorlistc) :: Rhos ! Tensor for singular values type(tensor) :: Tlam ! Singular values type(tensor) :: Lambda ! temporary tensors type(tensorc) :: Tmp, Tmpb, Tmpc ! Left transfer matrix for correlation measures type(tensorc) :: Ltheta ! Temporary operators type(tensorc) :: Tmpo ! Copy of MPS unit cell for mixed-canonical unit cell type(mpsc) :: Phi !if(present(errst)) errst = 0 qq = Psit(1)%ll bd = maxchi(Psit(1)) open(unit=obsunit, file=trim(obsname), status='replace', action='write') ! Write out correlation lengths - header of results write(obsunit, '(1I16)') errcode if(errcode /= 0) then close(obsunit) return end if write(obsunit, '(1I16)') ndeg write(obsunit, '(1I16)') size(Psit,1) write(obsunit, '(1I16)') bd write(obsunit, '(1E30.15)') MyObs%CorrelationLengths(1) write(obsunit, '(3E30.15)') of, err, oftol write(obsunit, '(1E30.15)') energy / (qq * 1.0_rKind) ! Allocate memory for correlators if(MyObs%CO%ncorr > 0) then allocate(corr(MyObs%CO%ncorr, 0:MyObs%corr_range)) end if if(MyObs%FCO%ncorr > 0) then allocate(fcorr(MyObs%FCO%ncorr, 0:MyObs%corr_range)) end if if(MyObs%STO%nstring > 0) then allocate(scorr(MyObs%STO%nstring, 0:MyObs%corr_range)) end if do pp = 1, size(Psit, 1) ! Generate mixed-canonical unit cell in Phi call copy(Phi, Psit(pp)) call contr(Tmp, Phi%Aa(qq), LambdaRs(pp), [3], [1], errst=errst) !if(prop_error('observe_infinite_mpsc : contr failed.', & ! 'iMPSOps_include.f90:3570', errst=errst)) return call destroy(Phi%Aa(qq)) call copy(Phi%Aa(qq), Tmp) if(MyObs%BE%bondentr) then ! Bond entropy - data point to the right ! ............ call svd(Tmpb, Tlam, Tmpc, Tmp, [1, 2], [3], errst=errst) !if(prop_error('observe_infinite_mpsc : svd '//& ! 'failed.', 'iMPSOps_include.f90:3581', errst=errst)) return call destroy(Tmpb) call destroy(Tmpc) call destroy(Tmp) Phi%haslambda(qq + 1) = .true. call copy(Phi%Lambda(qq + 1), Tlam) call lambdas_to_vec(Lambda, Tlam) call destroy(Tlam) Lambda%elem = Lambda%elem**2 do jj = 1, Lambda%dl(1) if(Lambda%elem(jj) > numzero) then MyObs%BE%elem(qq + 1) = MyObs%BE%elem(qq + 1) & - Lambda%elem(jj) & * log(Lambda%elem(jj)) end if end do call destroy(Lambda) else call destroy(Tmp) end if Phi%can(qq) = 'c' Phi%oc = qq ! Allocate list to store reduced density matrices call create(Rhos, qq) ! Reset correlation results (they are added to exising array) if(MyObs%CO%ncorr > 0) corr = 0.0_rKind if(MyObs%FCO%ncorr > 0) fcorr = 0.0_rKind if(MyObs%STO%nstring > 0) scorr = 0.0_rKind sites: do ii = qq, 1, (-1) if(ii /= Phi%oc) call canonize_svd(Phi, ii) if((ii < qq) .and. MyObs%BE%bondentr) then ! Bond entropy - data points in the bulk ! ............ call lambdas_to_vec(Lambda, Phi%Lambda(ii + 1)) Lambda%elem = Lambda%elem**2 do jj = 1, Lambda%dl(1) if(Lambda%elem(jj) > numzero) then MyObs%BE%elem(ii + 1) = MyObs%BE%elem(ii + 1) & - Lambda%elem(jj) & * log(Lambda%elem(jj)) end if end do call destroy(Lambda) end if call rho_kk(Rho, Phi, ii, errst=errst) !if(prop_error('observe_infinite_mpsc : rho_kk '//& ! 'failed.', 'iMPSOps_include.f90:3643', errst=errst)) return call copy(Rhos%Li(ii), Rho) if(MyObs%Ri%hasrho_i) then ! Single site density matrices ! ............................ idx = findtagindex(ii, MyObs%Ri%rho_i_i) if(idx > 0) call qmattomat(MyObs%Ri%Elem(ii), Rho, Imapper) end if ! Single-site observables ! ....................... local: do jj = 1, MyObs%SO%nsite MyObs%SO%elem(ii, jj) = MyObs%SO%Si(jj)%w & * real(trace_rho_x_mat(Rho, & Operators%Li(MyObs%SO%Si(jj)%o))) end do local ! Correlators (two-site) ! ...................... do jj = 1, MyObs%CO%ncorr idx = MyObs%CO%corrid(jj) ! Diagonal element call contr(Tmpo, Operators%Li(MyObs%CO%Corr(jj)%ol), & Operators%Li(MyObs%CO%Corr(jj)%or), [2], [1], & errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'contr failed.', 'iMPSOps_include.f90:3676', & ! errst=errst)) return call set_hash(Tmpo, [2], errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'set_hash failed.', 'iMPSOps_include.f90:3681', & ! errst=errst)) return corr(idx, 0) = corr(idx, 0) & + trace_rho_x_mat(Rhos%Li(ii), Tmpo) & * MyObs%CO%Corr(jj)%w call destroy(Tmpo) ! Propagate through the tensor network ! . . . . . . . . . . . . . . . . . . call copy(Tmp, Phi%Aa(ii)) call corr_init_l_mps(Tmp, Ltheta, & Operators%Li(MyObs%CO%Corr(jj)%or)) call destroy(Tmp) next = ii do kk = 1, MyObs%corr_range next = next - 1 if(next == 0) next = qq call corr_meas_l_mps(sc, Psit(pp)%Aa(next), & MyObs%corr_range + 1 - kk, Ltheta, & Operators%Li(MyObs%CO%Corr(jj)%ol), & Operators%Li(1), .false., errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'contr_diag failed.', 'iMPSOps_include.f90:3709', & ! errst=errst)) return corr(idx, kk) = corr(idx, kk) & + sc * MyObs%CO%Corr(jj)%w end do end do ! Fermi correlation functions ! ........................... do jj = 1, MyObs%FCO%ncorr idx = MyObs%FCO%corrid(jj) ! Diagonal element call contr(Tmpo, Operators%Li(MyObs%FCO%Corr(jj)%ol), & Operators%Li(MyObs%FCO%Corr(jj)%or), [2], [1], & errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'contr failed.', 'iMPSOps_include.f90:3728', & ! errst=errst)) return call set_hash(Tmpo, [2], errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'set_hash failed.', 'iMPSOps_include.f90:3733', & ! errst=errst)) return fcorr(idx, 0) = fcorr(idx, 0) & + trace_rho_x_mat(Rhos%Li(ii), Tmpo) & * MyObs%FCO%Corr(jj)%w call destroy(Tmpo) ! Propagate through the tensor network ! . . . . . . . . . . . . . . . . . . call copy(Tmp, Phi%Aa(ii)) call corr_init_l_mps(Tmp, Ltheta, & Operators%Li(MyObs%FCO%Corr(jj)%or)) call destroy(Tmp) next = ii do kk = 1, MyObs%corr_range next = next - 1 if(next == 0) next = qq call corr_meas_l_mps(sc, Psit(pp)%Aa(next), & MyObs%corr_range + 1 - kk, Ltheta, & Operators%Li(MyObs%FCO%Corr(jj)%ol), & Operators%Li(MyObs%FCO%fop), .true., errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'corr_meas failed.', 'iMPSOps_include.f90:3761', & ! errst=errst)) return fcorr(idx, kk) = fcorr(idx, kk) & + sc * MyObs%FCO%Corr(jj)%w end do end do ! String correlator functions ! ........................... do jj = 1, MyObs%STO%nstring ! Diagonal element call contr(Tmpo, Operators%Li(MyObs%STO%String(jj)%ol), & Operators%Li(MyObs%STO%String(jj)%or), & [2], [1], errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'contr failed.', 'iMPSOps_include.f90:3778', & ! errst=errst)) return call set_hash(Tmpo, [2], errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'set_hash failed.', 'iMPSOps_include.f90:3783', & ! errst=errst)) return scorr(idx, 0) = scorr(idx, 0) & + trace_rho_x_mat(Rhos%Li(ii), Tmpo) & * MyObs%STO%String(jj)%w call destroy(Tmpo) ! Propagate through the tensor network ! . . . . . . . . . . . . . . . . . . call copy(Tmp, Phi%Aa(ii)) call corr_init_l_mps(Tmp, Ltheta, & Operators%Li(MyObs%STO%String(jj)%or)) call destroy(Tmp) next = ii do kk = 1, MyObs%corr_range next = next - 1 if(next == 0) next = qq call corr_meas_l_mps(sc, Psit(pp)%Aa(next), & MyObs%corr_range + 1 - kk, Ltheta, & Operators%Li(MyObs%STO%String(jj)%ol), & Operators%Li(MyObs%STO%String(jj)%od), .true., & errst=errst) !if(prop_error('observe_infinite_mpsc : '//& ! 'corr_meas failed.', 'iMPSOps_include.f90:3812', & ! errst=errst)) return scorr(idx, kk) = scorr(idx, kk) & + sc * MyObs%STO%String(jj)%w end do end do ! Entropy single site (density matrix replaced with eigenvectors) ! ................... if(MyObs%SE%siteentr) then call entropy_rho_kk(MyObs%SE%elem(ii), Rho, errst=errst) end if call destroy(Rho) end do sites if(MyObs%BE%bondentr) then ! Bond entropy - data point to the left ! ............ call svd(Tmpb, Tlam, Tmpc, Phi%Aa(1), [1], [2, 3], errst=errst) !if(prop_error('observe_infinite_mpsc : svd '//& ! 'failed.', 'iMPSOps_include.f90:3837', errst=errst)) return call destroy(Tmpb) call destroy(Tmpc) call lambdas_to_vec(Lambda, Tlam) call destroy(Tlam) Lambda%elem = Lambda%elem**2 do jj = 1, Lambda%dl(1) if(Lambda%elem(jj) > numzero) then MyObs%BE%elem(1) = MyObs%BE%elem(1) & - Lambda%elem(jj) & * log(Lambda%elem(jj)) end if end do call destroy(Lambda) end if ! Deallocate list of all reduced single-site density matrices call destroy(Rhos) call destroy(Phi) ! Have to write all those results by hand ! --------------------------------------- ! Divide correlations by length of unit cell if(MyObs%CO%ncorr > 0) corr = corr / real(qq, KIND=rKind) if(MyObs%FCO%ncorr > 0) fcorr = fcorr / real(qq, KIND=rKind) if(MyObs%STO%nstring > 0) scorr = scorr / real(qq, KIND=rKind) ! Default string specifier for size of unit cell write(iwstring, '(I4)') qq specstring = "("//trim(adjustl(iwstring))//"E30.15E3)" call write(MyObs%SO, obsunit, specstring) call write(MyObs%SE, obsunit, specstring) call write(MyObs%BE, obsunit) ! Default string specifier for corr_range write(iwstring, '(I4)') MyObs%corr_range + 1 specstring = "("//trim(adjustl(iwstring))//"E30.15E3)" do jj = 1, MyObs%CO%ncorr if(MyObs%CO%isherm(jj)) then write(obsunit, '(1A1)') 'R' else write(obsunit, '(1A1)') 'C' end if write(obsunit, specstring) real(corr(jj, :), KIND=rKind) if(.not. MyObs%CO%isherm(jj)) then write(obsunit, specstring) aimag(corr(jj, :)) end if end do do jj = 1, MyObs%FCO%ncorr if(MyObs%FCO%isherm(jj)) then write(obsunit, '(1A1)') 'R' else write(obsunit, '(1A1)') 'C' end if write(obsunit, specstring) real(fcorr(jj, :), KIND=rKind) if(.not. MyObs%FCO%isherm(jj)) then write(obsunit, specstring) aimag(fcorr(jj, :)) end if end do do jj = 1, MyObs%STO%nstring write(obsunit, specstring) real(scorr(jj, :), KIND=rKind) end do end do ! Deallocate space for correlation measurements if(MyObs%CO%ncorr > 0) deallocate(corr) if(MyObs%FCO%ncorr > 0) deallocate(fcorr) if(MyObs%STO%nstring > 0) deallocate(scorr) close(obsunit) end subroutine observe_infinite_mpsc