KrylovOps¶
Fortran module KrylovOps: August 2017 (dj)
Contains the subroutines for propagating globally or locally the wave-function with the Krylov algorithm.
Authors
Jaschke
Wall
Details
Contains algorithms for Lanczos approach (Hamiltonians) and Arnoldi (Liouville operator for Lindblad master equation).
The following subroutines / functions are defined for the applicable data type
procedure |
include.f90 |
mpi.f90 |
|---|---|---|
krylov_method |
X |
- KrylovOps_f90.krylov_method_mpo_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(mpsc), inout
This is the wave function to be propagated.
- deltatcomplex, in
The time step for the evolution.
- HamTYPE(mpo), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_method_mpoc_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(mpsc), inout
This is the wave function to be propagated.
- deltatcomplex, in
The time step for the evolution.
- HamTYPE(mpoc), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_method_qmpo_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(qmpsc), inout
This is the wave function to be propagated.
- deltatcomplex, in
The time step for the evolution.
- HamTYPE(qmpo), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_method_qmpoc_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(qmpsc), inout
This is the wave function to be propagated.
- deltatcomplex, in
The time step for the evolution.
- HamTYPE(qmpoc), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_method_mpo_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(mps), inout
This is the wave function to be propagated.
- deltatreal, in
The time step for the evolution.
- HamTYPE(mpo), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_method_mpoc_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(mpsc), inout
This is the wave function to be propagated.
- deltatreal, in
The time step for the evolution.
- HamTYPE(mpoc), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_method_qmpo_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(qmps), inout
This is the wave function to be propagated.
- deltatreal, in
The time step for the evolution.
- HamTYPE(qmpo), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_method_qmpoc_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate the wave function Psi with the Krylov/Lanczos algorithm.
Arguments
- PsiTYPE(qmpsc), inout
This is the wave function to be propagated.
- deltatreal, in
The time step for the evolution.
- HamTYPE(qmpoc), inout
Evolve the wave function under this Hamiltonian.
- convergedLOGICAL, out
On exit, it indicates if the algorithm is converged within then given tolerances.
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- CpTYPE(ConvParam), inout
Stores all the convergence parameters necessary for the algorithm.
- init_randomCHARACTER, inout
Determines the initialization in the fit of H | psi >.
- renormLOGICAL, in
Flag if state vector should be renormalized to 1 (true). ‘N’ : do not normalize (default); ‘M’ : normalize for MPS 1 / sqrt(norm);
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_mpoc()[source]¶
fortran-subroutine - August 2017 (dj) Propagate Psi, possibly representing an MPDO, with the Arnoldi algorithm.
Arguments
- PsiTYPE(mpsc), inout
Propagate this MPS under the Hamiltonian passed as MPO and its parameters.
- deltatCOMPLEX, in
Time step for the evolution step (including -i)
- HTYPE(mpoc), inout
MPO representing the Hamiltonian.
- maxbonddINTEGER, inout
Maximal bond dimension
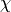 .
.- convergedLOGICAL, inout
Convergence flag of last subroutine called (FitMPS).
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- random_initCHARACTER, in
Flag for initial state of Fit_Hpsi.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability. (defined in TimeEvolutionOps_include.f90)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_qmpoc()[source]¶
fortran-subroutine - August 2017 (dj) Propagate Psi, possibly representing an MPDO, with the Arnoldi algorithm.
Arguments
- PsiTYPE(qmpsc), inout
Propagate this MPS under the Hamiltonian passed as MPO and its parameters.
- deltatCOMPLEX, in
Time step for the evolution step (including -i)
- HTYPE(qmpoc), inout
MPO representing the Hamiltonian.
- maxbonddINTEGER, inout
Maximal bond dimension
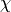 .
.- convergedLOGICAL, inout
Convergence flag of last subroutine called (FitMPS).
- cerrREAL, inout
The cumulated error. The error done during this subroutine is added to the incoming value.
- random_initCHARACTER, in
Flag for initial state of Fit_Hpsi.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
Currently uses complete reorthogonalization for stability. (defined in TimeEvolutionOps_include.f90)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_tensor_complex()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(tensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_tensor), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(tensorlistc), inout
Right overlap of MPS and MPO.
- deltatcomplex, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_tensorc_complex()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(tensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_tensorc), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(tensorlistc), inout
Right overlap of MPS and MPO.
- deltatcomplex, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_qtensor_complex()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(qtensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_qtensor), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(qtensorclist), inout
Right overlap of MPS and MPO.
- deltatcomplex, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_qtensorc_complex()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(qtensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_qtensorc), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(qtensorclist), inout
Right overlap of MPS and MPO.
- deltatcomplex, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_tensor_real()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(tensor), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_tensor), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(tensorlist), inout
Right overlap of MPS and MPO.
- deltatreal, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_tensorc_real()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(tensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_tensorc), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(tensorlistc), inout
Right overlap of MPS and MPO.
- deltatreal, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_qtensor_real()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(qtensor), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_qtensor), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(qtensorlist), inout
Right overlap of MPS and MPO.
- deltatreal, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_full_local_qtensorc_real()[source]¶
fortran-subroutine - September 2017 (dj, updated) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov.
Arguments
- PsiTYPE(qtensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_qtensorc), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(qtensorclist), inout
Right overlap of MPS and MPO.
- deltatreal, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Lanczos algorithm for hermitian Hamiltonians building the tridiagonal matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_full_local_tensor()[source]¶
fortran-subroutine - November 2017 (dj) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov-Arnoldi.
Arguments
- PsiTYPE(tensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_tensor), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(tensorlistc), inout
Right overlap of MPS and MPO.
- deltatDT_TYPE, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Arnoldi algorithm for general operators building the upper Hessenberg matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_full_local_tensorc()[source]¶
fortran-subroutine - November 2017 (dj) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov-Arnoldi.
Arguments
- PsiTYPE(tensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_tensorc), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(tensorlistc), inout
Right overlap of MPS and MPO.
- deltatDT_TYPE, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Arnoldi algorithm for general operators building the upper Hessenberg matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_full_local_qtensor()[source]¶
fortran-subroutine - November 2017 (dj) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov-Arnoldi.
Arguments
- PsiTYPE(qtensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_qtensor), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(qtensorclist), inout
Right overlap of MPS and MPO.
- deltatDT_TYPE, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Arnoldi algorithm for general operators building the upper Hessenberg matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_full_local_qtensorc()[source]¶
fortran-subroutine - November 2017 (dj) Propagate 1 or 2 site Hamiltonian with LR-overlaps and Krylov-Arnoldi.
Arguments
- PsiTYPE(qtensorc), inout
Tensor representing one or two sites of the MPS. Tensors is evolved under the MPO plus left-right-overlap.
- LL, inout
Left overlap of MPS and MPO.
- WmTYPE(sr_matrix_qtensorc), inout
The MPO matrix for one or two sites represented as sparse matrix.
- RRTYPE(qtensorclist), inout
Right overlap of MPS and MPO.
- deltatDT_TYPE, inout
Time step for the evolution. Complex for real time evolution and real for imaginary time evolution.
- leftmostLOGICAL, inout
Flag if subroutine is acting on the leftmost site.
- rightmostLOGICAL, inout
Flag if subroutine is acting on the rightmost site.
- CpTYPE(ConvParam), inout
Convergence parameters for the algorithm.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the Krylov-Arnoldi algorithm for general operators building the upper Hessenberg matrix in the Krylov subspace.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_tensor_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_tensorc_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_qtensor_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_qtensorc_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_tensor_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_tensorc_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_qtensor_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_local_qtensorc_real()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate a local two-site Hamiltonian with the Krylov algorithm. This version does not consider the left-right overlap.
Arguments
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
This version uses the two-site Hamiltonian in its tensor representation. Scaling is chi^2 d^4 for each Krylov step, and an additional d^4 kappa to build the two site Hamiltonian for this subroutine. Using the MPO representation, might speed things up to 2 chi^2 d^2 kappa. (kappa bond dimension of the MPO.)
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_local_tensor_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate an MPDO with the two-site Krylov-Arnoldi algorithm.
Arguments
- PsiTYPE(tensorc), inout
Represents the wave function of the tensor network. Has to contain the orthogonality center.
- HamTYPE(tensor), inout
The operator of which the exponential should be applied to the state Psi. Must be two-site Hamiltonian.
- deltatCOMPLEX, in
Time step for the time evolution.
- CpTYPE(ConvParam), in
Contains the convergence parameters for the algorithm. Subroutine accesses lanczos_tol and max_num_lanczos_iter.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
The Krylov-Arnoldi algorithm allows to propagate with non-hermitian two-site operators.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_local_tensorc_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate an MPDO with the two-site Krylov-Arnoldi algorithm.
Arguments
- PsiTYPE(tensorc), inout
Represents the wave function of the tensor network. Has to contain the orthogonality center.
- HamTYPE(tensorc), inout
The operator of which the exponential should be applied to the state Psi. Must be two-site Hamiltonian.
- deltatCOMPLEX, in
Time step for the time evolution.
- CpTYPE(ConvParam), in
Contains the convergence parameters for the algorithm. Subroutine accesses lanczos_tol and max_num_lanczos_iter.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
The Krylov-Arnoldi algorithm allows to propagate with non-hermitian two-site operators.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_local_qtensor_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate an MPDO with the two-site Krylov-Arnoldi algorithm.
Arguments
- PsiTYPE(qtensorc), inout
Represents the wave function of the tensor network. Has to contain the orthogonality center.
- HamTYPE(qtensor), inout
The operator of which the exponential should be applied to the state Psi. Must be two-site Hamiltonian.
- deltatCOMPLEX, in
Time step for the time evolution.
- CpTYPE(ConvParam), in
Contains the convergence parameters for the algorithm. Subroutine accesses lanczos_tol and max_num_lanczos_iter.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
The Krylov-Arnoldi algorithm allows to propagate with non-hermitian two-site operators.
Source Code
show / hide f90 code
- KrylovOps_f90.krylov_arnoldi_local_qtensorc_complex()[source]¶
fortran-subroutine - August 2017 (dj, updated) Propagate an MPDO with the two-site Krylov-Arnoldi algorithm.
Arguments
- PsiTYPE(qtensorc), inout
Represents the wave function of the tensor network. Has to contain the orthogonality center.
- HamTYPE(qtensorc), inout
The operator of which the exponential should be applied to the state Psi. Must be two-site Hamiltonian.
- deltatCOMPLEX, in
Time step for the time evolution.
- CpTYPE(ConvParam), in
Contains the convergence parameters for the algorithm. Subroutine accesses lanczos_tol and max_num_lanczos_iter.
- pbcLOGICAL, in
If PBC are used in any rule set. There is a check before, but the debugging mode should ensure for now that there are no calls with such a check.
Details
The Krylov-Arnoldi algorithm allows to propagate with non-hermitian two-site operators.
Source Code
show / hide f90 code