LinearAlgebra¶
Fortran module LinearAlgebra: May 2017 (dj)
Containing basic linear algebra operators defined for arrays.
Authors
Jaschke
Wall
Details
The following subroutines / functions are defined in the linear algebra module as interfaces.
Procedure |
|---|
diag_times_mat |
mat_times_diag |
diag_contr_tensor |
eigd |
eigsvd |
expm |
expmh |
kron |
trace_rho_x_mat |
tracematmul |
Various QR, RQ, and SVD are defined in addition.
- LinearAlgebra_f90.diag_times_mat_real_real()[source]¶
fortran-subroutine - November 2016 (dj) Multiplication of diagonal matrix with matrix.
Arguments
- matreal(nrow, ncol), inout
Matrix to be multiplied with diagonal matrix in vector form.
- diagreal(nrow), in
Diagonal matrix in vector form.
- nrowINTEGER, in
Number of rows in matrix and length of vector for diagonal matrix.
- ncolINTEGER, in
Number of columns in matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.diag_times_mat_complex_real()[source]¶
fortran-subroutine - November 2016 (dj) Multiplication of diagonal matrix with matrix.
Arguments
- matcomplex(nrow, ncol), inout
Matrix to be multiplied with diagonal matrix in vector form.
- diagreal(nrow), in
Diagonal matrix in vector form.
- nrowINTEGER, in
Number of rows in matrix and length of vector for diagonal matrix.
- ncolINTEGER, in
Number of columns in matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.diag_times_mat_complex_complex()[source]¶
fortran-subroutine - November 2016 (dj) Multiplication of diagonal matrix with matrix.
Arguments
- matcomplex(nrow, ncol), inout
Matrix to be multiplied with diagonal matrix in vector form.
- diagcomplex(nrow), in
Diagonal matrix in vector form.
- nrowINTEGER, in
Number of rows in matrix and length of vector for diagonal matrix.
- ncolINTEGER, in
Number of columns in matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.mat_times_diag_real_real()[source]¶
fortran-subroutine - November 2016 (dj) Multiplication of matrix with diagonal matrix.
Arguments
- matreal(nrow, ncol), inout
Matrix to be multiplied with diagonal matrix in vector form.
- diagreal(nrow), in
Diagonal matrix in vector form.
- nrowINTEGER, in
Number of rows in matrix.
- ncolINTEGER, in
Number of columns in matrix and length of vector for diagonal matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.mat_times_diag_complex_real()[source]¶
fortran-subroutine - November 2016 (dj) Multiplication of matrix with diagonal matrix.
Arguments
- matcomplex(nrow, ncol), inout
Matrix to be multiplied with diagonal matrix in vector form.
- diagreal(nrow), in
Diagonal matrix in vector form.
- nrowINTEGER, in
Number of rows in matrix.
- ncolINTEGER, in
Number of columns in matrix and length of vector for diagonal matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.mat_times_diag_complex_complex()[source]¶
fortran-subroutine - November 2016 (dj) Multiplication of matrix with diagonal matrix.
Arguments
- matcomplex(nrow, ncol), inout
Matrix to be multiplied with diagonal matrix in vector form.
- diagcomplex(nrow), in
Diagonal matrix in vector form.
- nrowINTEGER, in
Number of rows in matrix.
- ncolINTEGER, in
Number of columns in matrix and length of vector for diagonal matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.diag_contr_tensor_real_real()[source]¶
fortran-subroutine - November 2016 (dj) Contract a rank-three tensor with a diagonal matrix. Together with the diagonal matrix times matrix this covers all cases for contraction one index with a diagonal matrix.
Arguments
- tensreal(n1, n2, n3), inout
Rank three tensor to be contracted with diagonal matrix in vector form over second index.
- diagreal(n2), in
Diagonal matrix in vector form.
- n1INTEGER, in
Dimension of the first index of the tensor.
- n2INTEGER, in
Dimension of the second index of the tensor and the diagonal matrix.
- n3INTEGER, in
Dimension of the third index of the tensor.
Source Code
show / hide f90 code
- LinearAlgebra_f90.diag_contr_tensor_complex_real()[source]¶
fortran-subroutine - November 2016 (dj) Contract a rank-three tensor with a diagonal matrix. Together with the diagonal matrix times matrix this covers all cases for contraction one index with a diagonal matrix.
Arguments
- tenscomplex(n1, n2, n3), inout
Rank three tensor to be contracted with diagonal matrix in vector form over second index.
- diagreal(n2), in
Diagonal matrix in vector form.
- n1INTEGER, in
Dimension of the first index of the tensor.
- n2INTEGER, in
Dimension of the second index of the tensor and the diagonal matrix.
- n3INTEGER, in
Dimension of the third index of the tensor.
Source Code
show / hide f90 code
- LinearAlgebra_f90.diag_contr_tensor_complex_complex()[source]¶
fortran-subroutine - November 2016 (dj) Contract a rank-three tensor with a diagonal matrix. Together with the diagonal matrix times matrix this covers all cases for contraction one index with a diagonal matrix.
Arguments
- tenscomplex(n1, n2, n3), inout
Rank three tensor to be contracted with diagonal matrix in vector form over second index.
- diagcomplex(n2), in
Diagonal matrix in vector form.
- n1INTEGER, in
Dimension of the first index of the tensor.
- n2INTEGER, in
Dimension of the second index of the tensor and the diagonal matrix.
- n3INTEGER, in
Dimension of the third index of the tensor.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigd_symm_real()[source]¶
fortran-subroutine - April 2016 (dj) Diagonalize symmetric mata using LAPACK’s DSYEVD. Return the eigenvectors in mata, eigenvalues in ev.
Arguments
- mataREAL(,), inout
Diagonalize this matrix. On exit overwritten with eigenvectors.
- evREAL(*), out
Eigenvalues of diagonlization are stored in this vector.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigd_symm_complex()[source]¶
fortran-subroutine - April 2016 (dj) Diagonalize hermitian mata using LAPACK’s ZHEEV. Return the eigenvectors in mata, eigenvalues in ev.
Arguments
- mataCOMPLEX(,), inout
Diagonalize this matrix. On exit overwritten with eigenvectors.
- evREAL(*), out
Eigenvalues of diagonlization are stored in this vector.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigd_real()[source]¶
fortran-subroutine - November 2014 (dj) Diagonalization of a general real matrix
Arguments
- matREAL(,), inout
on input containing the matrix to be diagonalized on exit right eigenvectors of the matrix
- eivalCOMPLEX(*), out
containing on exit the (possibly complex) eigenvalues
- dimINTEGER, in
dimension of the eigenvalue problem.
- matinvREAL(,), OPTIONAL, out
containing on exit the inverse matrix of the right eigenvectors.
Details
The original matrix is regained with mat * eival * matinv (template defined in LinearAlgebra_template)
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigd_complex()[source]¶
fortran-subroutine - November 2014 (dj) Diagonalization of a general complex matrix
Arguments
- matCOMPLEX(,), inout
on input containing the matrix to be diagonalized on exit right eigenvectors of the matrix
- eivalCOMPLEX(*), out
containing on exit the (possibly complex) eigenvalues
- dimINTEGER, in
dimension of the eigenvalue problem.
- matinvCOMPLEX(,), OPTIONAL, out
containing on exit the inverse matrix of the right eigenvectors.
Details
The original matrix is regained with mat * eival * matinv (template defined in LinearAlgebra_template)
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigd_tri_symm_real()[source]¶
fortran-subroutine - April 2016 (dj) Diagonalize symmetric tridiagonal matrix with LAPACKs DSTEQR.
Arguments
- mataREAL(*, *), out
Contains on exit the eigenvectors of the symmetric tridiagonal matrix.
- diagREAL(*), inout
On entry the diagonal elements of the symmetric matrix, on exit the eigenvalues in ascending order.
- supdiagREAL(*), inout
Super-diagonal of the symmetric matrix. Destroyed on exit.
- dimINTEGER, in
Dimension of the square matrix
Details
(Template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigd_tri_symm_complex()[source]¶
fortran-subroutine - April 2016 (dj) Diagonalize hermitian tridiagonal matrix using LAPACKS dense method ZHEEV.
Arguments
- mataCOMPLEX(*, *), out
Contains on exit the eigenvectors of the symmetric tridiagonal matrix.
- diagREAL(*), inout
On entry the diagonal elements of the hermitian matrix, on exit the eigenvalues in ascending order.
- supdiagCOMPLEX(*), in
Super-diagonal of the hermitian matrix.
- dimINTEGER, in
Dimension of the square matrix
Details
(Template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigd_symm_tri_first_real()[source]¶
fortran-subroutine - July 2017 (dj, updated) Get the first eigenvalue and vector of a tridiagonal and real matrix.
Arguments
- diagsREAL(*), inout
The diagonal entries in the tridiagonal matrix.
- odiagsREAL(*), inout
The first off-diagonal entries in the triadiagonal matrix.
- eigvalREAL, out
The first eigenvalue.
- eigvecREAL(*), inout
The first eigenvector.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_lu_real()[source]¶
fortran-subroutine - Eigenvalue decomposition as singular value decomposition. ?? (dj, updated)
Arguments
- umreal(a_row, a_row), out
Unitary matrix for decomposition.
- singreal(a_row), out
Singular values (squared?)
- rmreal(a_row, a_col), out
Right matrix in decomposition, i.e., singular values times right unitary matrix.
- matinreal(a_row, a_col), in
Input matrix to be decomposed.
- a_rowINTEGER, in
Number of row in the original matrix.
- a_colINTEGER, in
Number of columns in the original matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_lu_complex()[source]¶
fortran-subroutine - Eigenvalue decomposition as singular value decomposition. ?? (dj, updated)
Arguments
- umcomplex(a_row, a_row), out
Unitary matrix for decomposition.
- singreal(a_row), out
Singular values (squared?)
- rmcomplex(a_row, a_col), out
Right matrix in decomposition, i.e., singular values times right unitary matrix.
- matincomplex(a_row, a_col), in
Input matrix to be decomposed.
- a_rowINTEGER, in
Number of row in the original matrix.
- a_colINTEGER, in
Number of columns in the original matrix.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_lu_step1_real()[source]¶
fortran-subroutine - ?? (dj, updated) First step of eigenvalue decomposition as singular value decomposition. This subroutine has the unitary matrix on the left.
Arguments
- umreal(a_row, a_row), out
Unitary matrix on the left of the decomposition on exit.
- singreal(a_row), out
Singular values squared on exit.
- matinreal(a_row, a_col), in
Input matrix to be decomposed.
- a_rowINTEGER, in
Number of rows in matrix to be decomposed
- a_colINTEGER, in
Number of columns in matrix to be decomposed.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_lu_step1_complex()[source]¶
fortran-subroutine - ?? (dj, updated) First step of eigenvalue decomposition as singular value decomposition. This subroutine has the unitary matrix on the left.
Arguments
- umcomplex(a_row, a_row), out
Unitary matrix on the left of the decomposition on exit.
- singreal(a_row), out
Singular values squared on exit.
- matincomplex(a_row, a_col), in
Input matrix to be decomposed.
- a_rowINTEGER, in
Number of rows in matrix to be decomposed
- a_colINTEGER, in
Number of columns in matrix to be decomposed.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_lu_step2_real()[source]¶
fortran-subroutine - ?? (dj, updated) Second step of eigenvalue decomposition as singular value decomposition. This subroutine has the unitary matrix on the left.
Arguments
- umreal(a_row, a_row), inout
Unitary matrix, modified in case of truncation.
- rtreal(nkeep, a_col), out
On exit, singular values times right unitary matrix.
- matinreal(a_row, a_col), in
Original matrix to be decomposed.
- a_rowINTEGER, in
Number of rows in original matrix.
- a_colINTEGER, in
Number of columns in original matrix.
- nkeepINTEGER, in
Number of singular values to be kept.
- renormREAL, OPTIONAL, in
Renormalization for decomposition (or scaling). Default to 1.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_lu_step2_complex()[source]¶
fortran-subroutine - ?? (dj, updated) Second step of eigenvalue decomposition as singular value decomposition. This subroutine has the unitary matrix on the left.
Arguments
- umcomplex(a_row, a_row), inout
Unitary matrix, modified in case of truncation.
- rtcomplex(nkeep, a_col), out
On exit, singular values times right unitary matrix.
- matincomplex(a_row, a_col), in
Original matrix to be decomposed.
- a_rowINTEGER, in
Number of rows in original matrix.
- a_colINTEGER, in
Number of columns in original matrix.
- nkeepINTEGER, in
Number of singular values to be kept.
- renormREAL, OPTIONAL, in
Renormalization for decomposition (or scaling). Default to 1.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_ru_step2_real()[source]¶
fortran-subroutine - Second step of eigenvalue decomposition as singular value decomposition. The unitary tensor is on the right.
Arguments
- umreal(*, *), in
Contains on exit the eigenvectors.
Source Code
show / hide f90 code
- LinearAlgebra_f90.eigsvd_ru_step2_complex()[source]¶
fortran-subroutine - Second step of eigenvalue decomposition as singular value decomposition. The unitary tensor is on the right.
Arguments
- umcomplex(*, *), in
Contains on exit the eigenvectors.
Source Code
show / hide f90 code
- LinearAlgebra_f90.expm_real_real()[source]¶
fortran-subroutine - April 2016 (dj) Take the exponential of a general matrix returning a complex matrix.
Arguments
- mexpcomplex(dim, dim), in
Exponential of the matrix sc * mat
- screal, in
Additional scalar inside exp-function.
- matreal(dim, dim), inout
On entry containing the matrix to be exponentiated. On exit destroyed (and filled with right eigenvectors).
- dimINTEGER, in
Dimension of the square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expm_complex_real()[source]¶
fortran-subroutine - April 2016 (dj) Take the exponential of a general matrix returning a complex matrix.
Arguments
- mexpcomplex(dim, dim), in
Exponential of the matrix sc * mat
- sccomplex, in
Additional scalar inside exp-function.
- matreal(dim, dim), inout
On entry containing the matrix to be exponentiated. On exit destroyed (and filled with right eigenvectors).
- dimINTEGER, in
Dimension of the square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expm_real_complex()[source]¶
fortran-subroutine - April 2016 (dj) Take the exponential of a general matrix returning a complex matrix.
Arguments
- mexpcomplex(dim, dim), in
Exponential of the matrix sc * mat
- screal, in
Additional scalar inside exp-function.
- matcomplex(dim, dim), inout
On entry containing the matrix to be exponentiated. On exit destroyed (and filled with right eigenvectors).
- dimINTEGER, in
Dimension of the square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expm_complex_complex()[source]¶
fortran-subroutine - April 2016 (dj) Take the exponential of a general matrix returning a complex matrix.
Arguments
- mexpcomplex(dim, dim), in
Exponential of the matrix sc * mat
- sccomplex, in
Additional scalar inside exp-function.
- matcomplex(dim, dim), inout
On entry containing the matrix to be exponentiated. On exit destroyed (and filled with right eigenvectors).
- dimINTEGER, in
Dimension of the square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_real_real()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc * math) for hermitian math.
Arguments
- mexpreal(dim, dim), out
Contains on exit exp(- eye * sc * math)
- screal, in
Weight in the exponential.
- matreal(*, *), inout
Take exponential of this hermitian matrix. On exit, overwritten with eigenvectors.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_complex_real()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc * math) for hermitian math.
Arguments
- mexpcomplex(dim, dim), out
Contains on exit exp(- eye * sc * math)
- sccomplex, in
Weight in the exponential.
- matreal(*, *), inout
Take exponential of this hermitian matrix. On exit, overwritten with eigenvectors.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_real_complex()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc * math) for hermitian math.
Arguments
- mexpcomplex(dim, dim), out
Contains on exit exp(- eye * sc * math)
- screal, in
Weight in the exponential.
- matcomplex(*, *), inout
Take exponential of this hermitian matrix. On exit, overwritten with eigenvectors.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_complex_complex()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc * math) for hermitian math.
Arguments
- mexpcomplex(dim, dim), out
Contains on exit exp(- eye * sc * math)
- sccomplex, in
Weight in the exponential.
- matcomplex(*, *), inout
Take exponential of this hermitian matrix. On exit, overwritten with eigenvectors.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_tri_real_real()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc* math) for hermitian tridiagonal matrix math.
Arguments
- mexpreal(dim, dim), out
Contains on exit exp(- eye * sc * mat)
- screal, in
Weight in the exponential.
- diagREAL(*), in
Diagonal entries of the matrix to be exponentiated.
- supdiagreal(*), in
Super-diagonal entries of the matrix to be exponentiated.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_tri_complex_real()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc* math) for hermitian tridiagonal matrix math.
Arguments
- mexpcomplex(dim, dim), out
Contains on exit exp(- eye * sc * mat)
- sccomplex, in
Weight in the exponential.
- diagREAL(*), in
Diagonal entries of the matrix to be exponentiated.
- supdiagreal(*), in
Super-diagonal entries of the matrix to be exponentiated.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_tri_real_complex()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc* math) for hermitian tridiagonal matrix math.
Arguments
- mexpcomplex(dim, dim), out
Contains on exit exp(- eye * sc * mat)
- screal, in
Weight in the exponential.
- diagREAL(*), in
Diagonal entries of the matrix to be exponentiated.
- supdiagcomplex(*), in
Super-diagonal entries of the matrix to be exponentiated.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.expmh_tri_complex_complex()[source]¶
fortran-subroutine - April 2016 (dj, updated) Exponentiate U=exp(sc* math) for hermitian tridiagonal matrix math.
Arguments
- mexpcomplex(dim, dim), out
Contains on exit exp(- eye * sc * mat)
- sccomplex, in
Weight in the exponential.
- diagREAL(*), in
Diagonal entries of the matrix to be exponentiated.
- supdiagcomplex(*), in
Super-diagonal entries of the matrix to be exponentiated.
- dimINTEGER, in
Dimension of the square matrix.
Details
(Template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
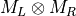 .
.Arguments
- Matreal(*, *), inout
On exit the tensor product between the two matrices. Has to be allocated on entry unless optional argument is set otherwise.
- Matl_real(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- Matrreal(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- translCHARACTER, in
Defines the transformation executed on the left matrix
 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).- transrCHARACTER, in
Defines the transformation executed on the left matrix
 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
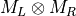 .
.Arguments
- Matcomplex(*, *), inout
On exit the tensor product between the two matrices. Has to be allocated on entry unless optional argument is set otherwise.
- Matl_complex(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- Matrcomplex(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- translCHARACTER, in
Defines the transformation executed on the left matrix
 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).- transrCHARACTER, in
Defines the transformation executed on the left matrix
 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
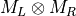 .
.Arguments
- Matcomplex(*, *), inout
On exit the tensor product between the two matrices. Has to be allocated on entry unless optional argument is set otherwise.
- Matl_real(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- Matrreal(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- translCHARACTER, in
Defines the transformation executed on the left matrix
 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).- transrCHARACTER, in
Defines the transformation executed on the left matrix
 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mm_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
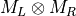 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mm_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
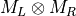 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mm_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
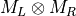 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mmt_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
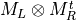 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is transposed while
taking tensor product.
in the tensor product. Is transposed while
taking tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mmt_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
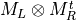 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product. Is transposed while
taking tensor product.
in the tensor product. Is transposed while
taking tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mmt_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
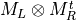 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is transposed while
taking tensor product.
in the tensor product. Is transposed while
taking tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mmd_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
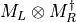 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is daggered while
taking tensor product.
in the tensor product. Is daggered while
taking tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mmd_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
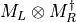 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product. Is daggered while
taking tensor product.
in the tensor product. Is daggered while
taking tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mmd_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
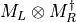 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is daggered while
taking tensor product.
in the tensor product. Is daggered while
taking tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtm_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
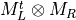 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is transposed while
taking the tensor product.
in the tensor product. Is transposed while
taking the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtm_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
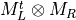 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product. Is transposed while
taking the tensor product.
in the tensor product. Is transposed while
taking the tensor product.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtm_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
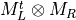 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is transposed while
taking the tensor product.
in the tensor product. Is transposed while
taking the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdm_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
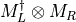 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is daggered while
taking the tensor product.
in the tensor product. Is daggered while
taking the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdm_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
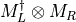 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product. Is daggered while
taking the tensor product.
in the tensor product. Is daggered while
taking the tensor product.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdm_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
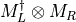 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. Is daggered while
taking the tensor product.
in the tensor product. Is daggered while
taking the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtmt_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
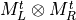 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtmt_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
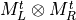 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtmt_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
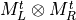 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product.
in the tensor product.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdmd_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
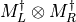 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered during the
subroutine.
in the tensor product. It is daggered during the
subroutine.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered during the
subroutine.
in the tensor product. It is daggered during the
subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdmd_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
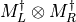 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product. It is daggered during the
subroutine.
in the tensor product. It is daggered during the
subroutine.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product. It is daggered during the
subroutine.
in the tensor product. It is daggered during the
subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdmd_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
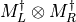 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered during the
subroutine.
in the tensor product. It is daggered during the
subroutine.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered during the
subroutine.
in the tensor product. It is daggered during the
subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdmt_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
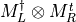 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered
during the subroutine.
in the tensor product. It is daggered
during the subroutine.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is transposed
during the subroutine.
in the tensor product. It is transposed
during the subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdmt_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
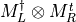 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product. It is daggered
during the subroutine.
in the tensor product. It is daggered
during the subroutine.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product. It is transposed
during the subroutine.
in the tensor product. It is transposed
during the subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdmt_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
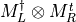 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered
during the subroutine.
in the tensor product. It is daggered
during the subroutine.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is transposed
during the subroutine.
in the tensor product. It is transposed
during the subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtmd_real_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
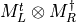 .
.Arguments
- matTYPE(real)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is transposed
during the subroutine.
in the tensor product. It is transposed
during the subroutine.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered
during the subroutine.
in the tensor product. It is daggered
during the subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtmd_complex_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
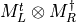 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(complex)(*, *), in
Left matrix
 in the tensor product. It is transposed
during the subroutine.
in the tensor product. It is transposed
during the subroutine.- mat2TYPE(complex)(*, *), in
Left matrix
 in the tensor product. It is daggered
during the subroutine.
in the tensor product. It is daggered
during the subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mtmd_complex_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between two matrices
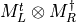 .
.Arguments
- matTYPE(complex)(*, *), inout
On exit the tensor product between the two matrices.
- mat1TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is transposed
during the subroutine.
in the tensor product. It is transposed
during the subroutine.- mat2TYPE(real)(*, *), in
Left matrix
 in the tensor product. It is daggered
during the subroutine.
in the tensor product. It is daggered
during the subroutine.- r1INTEGER, in
First dimension of

- c1INTEGER, in
Second dimension of

- r2INTEGER, in
First dimension of

- c2INTEGER, in
Second dimension of

- opCHARACTER, in
Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_id_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity, so either
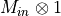 or
or 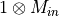 .
.Arguments
- matreal(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- matinreal(*, *), in
Matrix in the tensor product with the identity
- d1INTEGER, in
First dimension of matin.
- d2INTEGER, in
Second dimension of matin.
- didINTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- idCHARACTER, in
Defines the position of the identity matrix. Either ‘L’ for
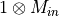 or ‘R’ for
or ‘R’ for 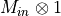 .
.- transCHARACTER, in
Defines the transformation executed on matrix
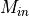 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_id_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity, so either
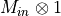 or
or 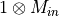 .
.Arguments
- matcomplex(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- matincomplex(*, *), in
Matrix in the tensor product with the identity
- d1INTEGER, in
First dimension of matin.
- d2INTEGER, in
Second dimension of matin.
- didINTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- idCHARACTER, in
Defines the position of the identity matrix. Either ‘L’ for
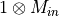 or ‘R’ for
or ‘R’ for 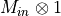 .
.- transCHARACTER, in
Defines the transformation executed on matrix
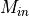 when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed),
or ‘D’ (dagger / conjugate transposed).
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mi_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
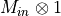 .
.Arguments
- matreal(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat1real(*, *), in
Matrix in the tensor product with the identity
- r1INTEGER, in
First dimension of the matrix.
- c1INTEGER, in
Second dimension of the matrix.
- d2INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mi_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
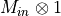 .
.Arguments
- matcomplex(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat1complex(*, *), in
Matrix in the tensor product with the identity
- r1INTEGER, in
First dimension of the matrix.
- c1INTEGER, in
Second dimension of the matrix.
- d2INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_im_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
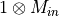 .
.Arguments
- matreal(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat2real(*, *), in
Matrix in the tensor product with the identity
- d1INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- r2INTEGER, in
First dimension of the matrix.
- c2INTEGER, in
Second dimension of the matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_im_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
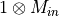 .
.Arguments
- matcomplex(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat2complex(*, *), in
Matrix in the tensor product with the identity
- d1INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- r2INTEGER, in
First dimension of the matrix.
- c2INTEGER, in
Second dimension of the matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mti_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
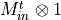 .
.Arguments
- matreal(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat1real(*, *), in
Matrix in the tensor product with the identity. Transposed while taking the tensor product.
- r1INTEGER, in
First dimension of the matrix.
- c1INTEGER, in
Second dimension of the matrix.
- d2INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mti_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
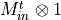 .
.Arguments
- matcomplex(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat1complex(*, *), in
Matrix in the tensor product with the identity. Transposed while taking the tensor product.
- r1INTEGER, in
First dimension of the matrix.
- c1INTEGER, in
Second dimension of the matrix.
- d2INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_imt_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
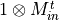 .
.Arguments
- matreal(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat2real(*, *), in
Matrix in the tensor product with the identity. Transposed while taking tensor product.
- d1INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- r2INTEGER, in
First dimension of the matrix.
- c2INTEGER, in
Second dimension of the matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_imt_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
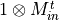 .
.Arguments
- matcomplex(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat2complex(*, *), in
Matrix in the tensor product with the identity. Transposed while taking tensor product.
- d1INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- r2INTEGER, in
First dimension of the matrix.
- c2INTEGER, in
Second dimension of the matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdi_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
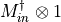 .
.Arguments
- matreal(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat1real(*, *), in
Matrix in the tensor product with the identity. Daggered while taking the tensor product.
- r1INTEGER, in
First dimension of the matrix.
- c1INTEGER, in
Second dimension of the matrix.
- d2INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_mdi_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
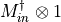 .
.Arguments
- matcomplex(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat1complex(*, *), in
Matrix in the tensor product with the identity. Daggered while taking the tensor product.
- r1INTEGER, in
First dimension of the matrix.
- c1INTEGER, in
Second dimension of the matrix.
- d2INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_imd_real()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
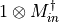 .
.Arguments
- matreal(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat2real(*, *), in
Matrix in the tensor product with the identity. Daggered while taking tensor product.
- d1INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- r2INTEGER, in
First dimension of the matrix.
- c2INTEGER, in
Second dimension of the matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.kron_imd_complex()[source]¶
fortran-subroutine - May 2016 (dj) Kronecker or tensor product between a matrix and the identity
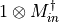 .
.Arguments
- matcomplex(*, *), in
On exit the tensor product between the two matrices. Has to be allocated on entry.
- mat2complex(*, *), in
Matrix in the tensor product with the identity. Daggered while taking tensor product.
- d1INTEGER, in
Specifies the dimension of the identity matrix. Alwyas square matrix.
- r2INTEGER, in
First dimension of the matrix.
- c2INTEGER, in
Second dimension of the matrix.
Details
(template defined in LinearAlgebra_include.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.qr_inplace_real()[source]¶
fortran-subroutine - September 2014 (dj) Compute thin QR-decomposition inplace for nxm-matrix with n >=m
Arguments
- matREAL(ld_mat, *), inout
Matrix to be deomposed in QR with nr >= nc. On exit matrix Q.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatREAL(nc, *), out
On exit triangular matrix R of QR-decomposition.
Details
(template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.qr_trapez_real()[source]¶
fortran-subroutine - April 2016 (dj) Compute thin QR-decomposition inplace for nxm-matrix with n < m
Arguments
- matREAL(ld_mat, *), inout
Matrix to be deomposed in QR with nr < nc. On exit entries are destroyed.
- qmatREAL(nr, nr), out
On exit, unitary matrix Q of QR-decomposition.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatREAL(nc, *), out
On exit triangular matrix R of QR-decomposition.
Details
(template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.qr_inplace_complex()[source]¶
fortran-subroutine - September 2014 (dj) Compute thin QR-decomposition inplace for nxm-matrix with n >=m
Arguments
- matCOMPLEX(ld_mat, *), inout
Matrix to be deomposed in QR with nr >= nc. On exit matrix Q.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatCOMPLEX(nc, *), out
On exit triangular matrix R of QR-decomposition.
Details
(template defined in LinearAlgebar_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.qr_trapez_complex()[source]¶
fortran-subroutine - April 2016 (dj) Compute thin QR-decomposition inplace for nxm-matrix with n >=m
Arguments
- matCOMPLEX(ld_mat, *), inout
Matrix to be deomposed in QR with nr < nc. On exit entries are destroyed.
- qmatCOMPLEX(nr, nr), out
On exit, unitary matrix Q of QR decomposition.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatCOMPLEX(nc, *), out
On exit triangular matrix R of QR-decomposition.
Details
(template defined in LinearAlgebar_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.rq_inplace_real()[source]¶
fortran-subroutine - September 2014 (dj) Compute thin RQ-decomposition inplace for nxm-matrix with n <= m
Arguments
- matREAL(ld_mat, *), inout
Matrix to be deomposed in RQ with nr <= nc. On exit matrix Q.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatREAL(nc, *), out
On exit triangular matrix R of RQ-decomposition.
Details
(template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.rq_trapez_real()[source]¶
fortran-subroutine - April 2016 (dj) Compute thin RQ-decomposition inplace for nxm-matrix with n > m
Arguments
- matREAL(ld_mat, *), inout
Matrix to be deomposed in RQ with nr > nc. On exit entries are destroyed.
- qmatREAL(nc, nc), out
On exit, qmat is unitary matrix Q or RQ-decomposition.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatREAL(nc, *), out
On exit triangular matrix R of RQ-decomposition.
Details
(template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.rq_inplace_complex()[source]¶
fortran-subroutine - September 2014 (dj) Compute thin RQ-decomposition inplace for nxm-matrix with n <= m
Arguments
- matCOMPLEX(ld_mat, *), inout
Matrix to be deomposed in RQ with nr <= nc. On exit matrix Q.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatCOMPLEX(nc, *), out
On exit triangular matrix R of RQ-decomposition.
Details
(template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.rq_trapez_complex()[source]¶
fortran-subroutine - April 2016 (dj) RQ-decomposition for the case that complex matrix has more rows than colums.
Arguments
- matCOMPLEX(ld_mat, *), inout
Matrix to be deomposed in RQ with nr > nc. On exit entries destroyed.
- qmatCOMPLEX(nc, nc), inout
On exit, unitary matrix Q of RQ decomposition.
- nrINTEGER, in
number of rows in mat
- ncINTEGER, in
number of columns in mat
- ld_matINTEGER, in
leading dimension of the array mat
- rmatCOMPLEX(nc, *), out
On exit triangular matrix R of RQ-decomposition.
Details
(template defined in LinearAlgebra_template.f90)
Source Code
show / hide f90 code
- LinearAlgebra_f90.svd_elem_real()[source]¶
fortran-subroutine - September 2014 (dj) Perform a SVD without truncation on real arrays with DGESVD
Arguments
- uleftREAL(*, *), out
on exit the left unitary matrix
- singREAL(*), out
contains on exit the singular values
- vrightREAL(*,*), out
on exit the right unitary matrix
- matinREAL(*,*), inout
contains the matrix to be decomposed in a SVD. On exit the entries are destroyed.
- a_rowINTEGER, in
number of rows in matrix matin
- a_colINTEGER, in
number of columns in matin
- infoINTEGER, inout
exit status of ZGESDD (0: sucessful, <0 : wrong argument, >0 : not converged)
Source Code
show / hide f90 code
- LinearAlgebra_f90.svdd_elem_real()[source]¶
fortran-subroutine - September 2014 (dj) Perform an SVD without truncation on real arrays with DGESDD.
Arguments
- uREAL(*, *), out
on exit the left unitary matrix
- sREAL(*), out
contains on exit the singular values
- vREAL(*,*), out
on exit the right unitary matrix
- aREAL(*,*), inout
contains the matrix to be decomposed in a SVD. On exit the entries are destroyed.
- a_rowINTEGER, in
number of rows in matrix a
- a_colINTEGER, in
number of columns in a
- jobzCHARACTER, in
‘O’ : either U or VT are written in input matrix a ‘S’ : economic SVD without overwritting ‘A’ : all rows/columns in U and VT are calculated ‘N’ : only singular values further see LAPACK description
- infoINTEGER, inout
exit status of ZGESDD (0: sucessful, <0: wrong argument, >0: not converged)
Source Code
show / hide f90 code
- LinearAlgebra_f90.svd_elem_complex()[source]¶
fortran-subroutine - September 2014 (dj) Perform a SVD without truncation on complex arrays with ZGESVD
Arguments
- uleftCOMPLEX(*, *), out
on exit the left unitary matrix
- singREAL(*), out
contains on exit the singular values
- vrightCOMPLEX(*,*), out
on exit the right unitary matrix
- matinCOMPLEX(*,*), inout
contains the matrix to be decomposed in a SVD. On exit the entries are destroyed.
- a_rowINTEGER, in
number of rows in matrix matin
- a_colINTEGER, in
number of columns in matin
- infoINTEGER, inout
exit status of ZGESDD (0: sucessful, <0: wrong argument, >0: not converged)
Source Code
show / hide f90 code
- LinearAlgebra_f90.svdd_elem_complex()[source]¶
fortran-subroutine - September 2014 (dj) Perform a SVD without truncation on complex arrays with ZGESDD
Arguments
- uCOMPLEX(*, *), out
on exit the left unitary matrix
- sREAL(*), out
contains on exit the singular values
- vCOMPLEX(*,*), out
on exit the right unitary matrix
- aCOMPLEX(*,*), inout
contains the matrix to be decomposed in a SVD. On exit the entries are destroyed.
- a_rowINTEGER, in
number of rows in matrix a
- a_colINTEGER, in
number of columns in a
- jobzCHARACTER, in
‘O’ : either U or VT are written in input matrix a ‘S’ : economic SVD without overwritting ‘A’ : all rows/columns in U and VT are calculated ‘N’ : only singular values further see LAPACK description
- infoINTEGER, inout
exit status of ZGESDD (0: sucessful, <0: wrong argument, >0: not converged)
Source Code
show / hide f90 code
- LinearAlgebra_f90.trace_rho_x_mat_real_real()[source]¶
fortran-function - November 2016 (dj) Trace of the matrix-matrix multiplication of a density matrix and a matrix.
Arguments
- rhoRHO_TYOE(*, *), in
Density matrix. Must be hermitian since this property is used.
- matreal(*, *), in
Operator matrix.
- dimINTEGER, in
Dimension of the two square matrices.
Source Code
show / hide f90 code
- LinearAlgebra_f90.trace_rho_x_mat_complex_real()[source]¶
fortran-function - November 2016 (dj) Trace of the matrix-matrix multiplication of a density matrix and a matrix.
Arguments
- rhoRHO_TYOE(*, *), in
Density matrix. Must be hermitian since this property is used.
- matreal(*, *), in
Operator matrix.
- dimINTEGER, in
Dimension of the two square matrices.
Source Code
show / hide f90 code
- LinearAlgebra_f90.trace_rho_x_mat_complex_complex()[source]¶
fortran-function - November 2016 (dj) Trace of the matrix-matrix multiplication of a density matrix and a matrix.
Arguments
- rhoRHO_TYOE(*, *), in
Density matrix. Must be hermitian since this property is used.
- matcomplex(*, *), in
Operator matrix.
- dimINTEGER, in
Dimension of the two square matrices.
Source Code
show / hide f90 code
- LinearAlgebra_f90.tracematmul_real()[source]¶
fortran-function - November 2017 (dj) Calculate the trace of a matrix multiplication without contructing the intermediate matrix.
Arguments
- matlreal(*, *), in
Left matrix in the multiplication.
- matrreal(*, *), in
Right matrix in the multuplication.
- dimINTEGER, in
Dimension of the square matrices (right now we restrict the function to square matrices).
- translCHARACTER, in
Transformation of the left matrix. ‘N’ for no transformation, ‘T’ for transposed, and ‘C’ for the hermitian conjugated.
- transrCHARACTER, in
Transformation of the right matrix. ‘N’ for no transformation, ‘T’ for transposed, and ‘C’ for the hermitian conjugated.
Source Code
show / hide f90 code
- LinearAlgebra_f90.tracematmul_complex()[source]¶
fortran-function - November 2017 (dj) Calculate the trace of a matrix multiplication without contructing the intermediate matrix.
Arguments
- matlcomplex(*, *), in
Left matrix in the multiplication.
- matrcomplex(*, *), in
Right matrix in the multuplication.
- dimINTEGER, in
Dimension of the square matrices (right now we restrict the function to square matrices).
- translCHARACTER, in
Transformation of the left matrix. ‘N’ for no transformation, ‘T’ for transposed, and ‘C’ for the hermitian conjugated.
- transrCHARACTER, in
Transformation of the right matrix. ‘N’ for no transformation, ‘T’ for transposed, and ‘C’ for the hermitian conjugated.
Source Code
show / hide f90 code