Tensors¶

Fortran module Tensors: June 2017 (dj)

Containing basic operations for tensors as allocation, reading writing.

Authors

1. Jaschke
1. 1. Wall

Details

The error status can be decoded the following way

1: allocation / deallocation problem
2: rank mismatch
3: dimension mismatch
4: unknown argument
5: argument not valid

The following subroutines / functions are defined for the applicable data type

procedure	include.f90	mpi.f90
addproject	X
add_dummylink	X
conj	X
copy	X
create	X
create_id	X
dagger	X
destroy	X
dot	X
equals	X
expm	X
expmh	X
finalize (splitlink)	X
fuse	X
gaxpy	X
get_scalar	X
has_nan	X
init (splitlink)	X
is_eye	X
is_set	X
kron	X
maxlineardim	X
maxvalue	X
norm	X
par_recv		X
par_send		X
permute	X
perturb	X
pointto	X
print	X
project	X
qmattomat	X
randomize	X
rank	X
read	X
scale	X
set_hash	X
split	X
trace	X
transposed	X
write	X
write_as_matrix	X

Tensors_f90.addProject_tensor()[source]¶

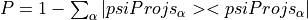fortran-subroutine - March 2016 (updated dj) Apply the projector P to A and add to B, where P is defined as $P = 1-\sum_{\alpha}|psiProjs_{\alpha}><psiProjs_{\alpha}|$ .

Arguments

BbTYPE(tensor), inout: Add projection of A to this tensor.
AaTYPE(tensor), in: Get projection of this tensor and add to Bb
PsiProjsTYPE(tensor)(*), in: Array of tensors defining the projector.

Details

Used in orthogonalizing an MPS against another set of MPSs.

Source Code

show / hide f90 code

Tensors_f90.addProject_tensorc()[source]¶

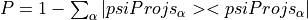fortran-subroutine - March 2016 (updated dj) Apply the projector P to A and add to B, where P is defined as $P = 1-\sum_{\alpha}|psiProjs_{\alpha}><psiProjs_{\alpha}|$ .

Arguments

BbTYPE(tensorc), inout: Add projection of A to this tensor.
AaTYPE(tensorc), in: Get projection of this tensor and add to Bb
PsiProjsTYPE(tensorc)(*), in: Array of tensors defining the projector.

Details

Used in orthogonalizing an MPS against another set of MPSs.

Source Code

show / hide f90 code

Tensors_f90.add_dummylink_tensor()[source]¶

fortran-subroutine - October 2017 (dj) Add a dummy link to a tensor.

Arguments

TensTYPE(tensor), inout: Add a dummy link of dimenions one to the tensor.
idxINTEGER, in: Position of the dummy link in the modified tensor.

Source Code

show / hide f90 code

Tensors_f90.add_dummylink_tensorc()[source]¶

fortran-subroutine - October 2017 (dj) Add a dummy link to a tensor.

Arguments

TensTYPE(tensorc), inout: Add a dummy link of dimenions one to the tensor.
idxINTEGER, in: Position of the dummy link in the modified tensor.

Source Code

show / hide f90 code

Tensors_f90.check_qnum_tensdim_tensor()[source]¶

fortran-subroutine - August 2018 (dj) Dummy routine to comply with qTensors.

Arguments

TensTYPE(Qtensor), in: Tensor to be checked. Nothing to check.

Source Code

show / hide f90 code

Tensors_f90.check_qnum_tensdim_tensorc()[source]¶

fortran-subroutine - August 2018 (dj) Dummy routine to comply with qTensors.

Arguments

TensTYPE(Qtensorc), in: Tensor to be checked. Nothing to check.

Source Code

show / hide f90 code

Tensors_f90.conj_tensor()[source]¶

fortran-subroutine - October 2016 (dj) Complex-conjugated elements in the tensor.

Arguments

TensTYPE(tensor), inout: Take the complex conjugate of each element

Source Code

show / hide f90 code

Tensors_f90.conj_tensorc()[source]¶

fortran-subroutine - October 2016 (dj) Complex-conjugated elements in the tensor.

Arguments

TensTYPE(tensorc), inout: Take the complex conjugate of each element

Source Code

show / hide f90 code

Tensors_f90.copy_tensor_tensor()[source]¶

fortran-subroutine - October 2016 (dj) Copy a tensor.

Arguments

TensoutTYPE(tensor), out: Store copy of Tensin in this tensor.
TensinTYPE(tensor), in: Copy this tensor to a new tensor Tensout.
scalarreal, OPTIONAL, in: Multiply input tensor with scalar during copying replacing a copy + scale action.
transCHARACTER, OPTIONAL, in: The following transformation can be applied: complex conjugate (‘C’), transposition (‘T’, simple transposition, no permutation), conjugate transposed (‘H’, simple transposition). No transformation is ‘N’. Default to ‘N’.

Source Code

show / hide f90 code

  subroutine copy_tensor_tensor(Tensout, Tensin, scalar, trans, &
                                           errst)
      type(tensor), intent(out) :: Tensout
      type(tensor), intent(in) :: Tensin
      real(KIND=rKind), intent(in), optional :: scalar
      character, intent(in), optional :: trans
      integer, intent(out), optional :: errst

      !if(Tensin%rank == -1) then
      !    errst = raise_error('copy_tensor_tensor: '//&
      !                        'Tensin empty.', 99, 'Tensors_include.f90:263', &
      !                        errst=errst)
      !    return
      !end if

      call create(Tensout, Tensin%dl, errst=errst)
      !if(prop_error('copy_tensor_tensor: create failed.', &
      !              'Tensors_include.f90:270', errst=errst)) return

      if(present(scalar)) then
          Tensout%elem(:Tensin%dim) = scalar * Tensin%elem(:Tensin%dim)
      else
          Tensout%elem(:Tensin%dim) = Tensin%elem(:Tensin%dim)
      end if

      ! No transformation
      if(.not. present(trans)) return

      ! Check which transformation is applied
      if(trans == 'C') then
          call conj(Tensout, errst)
          !if(prop_error('copy_tensor_tensor:'//&
          !              ' conjg failed.', 'Tensors_include.f90:285', &
          !              errst=errst)) return

      elseif(trans == 'T') then
          call transposed(Tensout, errst=errst)
          !if(prop_error('copy_tensor_tensor:'//&
          !              ' transpose failed.', 'Tensors_include.f90:291', &
          !              errst=errst)) return

      elseif(trans == 'H') then
          call dagger(Tensout, errst=errst)
          !if(prop_error('copy_tensor_tensor:'//&
          !              'dagger failed.', 'Tensors_include.f90:297', &
          !              errst=errst)) return

      elseif(trans /= 'N') then
          !errst = raise_error('copy_tensor_tensor:'//&
          !                    ' unknown argument trans.', 4, &
          !                    'Tensors_include.f90:303', errst=errst)
      end if

  end subroutine copy_tensor_tensor

Tensors_f90.copy_tensorc_tensor()[source]¶

fortran-subroutine - October 2016 (dj) Copy a tensor.

Arguments

TensoutTYPE(tensorc), out: Store copy of Tensin in this tensor.
TensinTYPE(tensor), in: Copy this tensor to a new tensor Tensout.
scalarcomplex, OPTIONAL, in: Multiply input tensor with scalar during copying replacing a copy + scale action.
transCHARACTER, OPTIONAL, in: The following transformation can be applied: complex conjugate (‘C’), transposition (‘T’, simple transposition, no permutation), conjugate transposed (‘H’, simple transposition). No transformation is ‘N’. Default to ‘N’.

Source Code

show / hide f90 code

  subroutine copy_tensorc_tensor(Tensout, Tensin, scalar, trans, &
                                           errst)
      type(tensorc), intent(out) :: Tensout
      type(tensor), intent(in) :: Tensin
      complex(KIND=rKind), intent(in), optional :: scalar
      character, intent(in), optional :: trans
      integer, intent(out), optional :: errst

      !if(Tensin%rank == -1) then
      !    errst = raise_error('copy_tensorc_tensor: '//&
      !                        'Tensin empty.', 99, 'Tensors_include.f90:263', &
      !                        errst=errst)
      !    return
      !end if

      call create(Tensout, Tensin%dl, errst=errst)
      !if(prop_error('copy_tensorc_tensor: create failed.', &
      !              'Tensors_include.f90:270', errst=errst)) return

      if(present(scalar)) then
          Tensout%elem(:Tensin%dim) = scalar * Tensin%elem(:Tensin%dim)
      else
          Tensout%elem(:Tensin%dim) = Tensin%elem(:Tensin%dim)
      end if

      ! No transformation
      if(.not. present(trans)) return

      ! Check which transformation is applied
      if(trans == 'C') then
          call conj(Tensout, errst)
          !if(prop_error('copy_tensorc_tensor:'//&
          !              ' conjg failed.', 'Tensors_include.f90:285', &
          !              errst=errst)) return

      elseif(trans == 'T') then
          call transposed(Tensout, errst=errst)
          !if(prop_error('copy_tensorc_tensor:'//&
          !              ' transpose failed.', 'Tensors_include.f90:291', &
          !              errst=errst)) return

      elseif(trans == 'H') then
          call dagger(Tensout, errst=errst)
          !if(prop_error('copy_tensorc_tensor:'//&
          !              'dagger failed.', 'Tensors_include.f90:297', &
          !              errst=errst)) return

      elseif(trans /= 'N') then
          !errst = raise_error('copy_tensorc_tensor:'//&
          !                    ' unknown argument trans.', 4, &
          !                    'Tensors_include.f90:303', errst=errst)
      end if

  end subroutine copy_tensorc_tensor

Tensors_f90.copy_tensorc_tensorc()[source]¶

fortran-subroutine - October 2016 (dj) Copy a tensor.

Arguments

TensoutTYPE(tensorc), out: Store copy of Tensin in this tensor.
TensinTYPE(tensorc), in: Copy this tensor to a new tensor Tensout.
scalarcomplex, OPTIONAL, in: Multiply input tensor with scalar during copying replacing a copy + scale action.
transCHARACTER, OPTIONAL, in: The following transformation can be applied: complex conjugate (‘C’), transposition (‘T’, simple transposition, no permutation), conjugate transposed (‘H’, simple transposition). No transformation is ‘N’. Default to ‘N’.

Source Code

show / hide f90 code

  subroutine copy_tensorc_tensorc(Tensout, Tensin, scalar, trans, &
                                           errst)
      type(tensorc), intent(out) :: Tensout
      type(tensorc), intent(in) :: Tensin
      complex(KIND=rKind), intent(in), optional :: scalar
      character, intent(in), optional :: trans
      integer, intent(out), optional :: errst

      !if(Tensin%rank == -1) then
      !    errst = raise_error('copy_tensorc_tensorc: '//&
      !                        'Tensin empty.', 99, 'Tensors_include.f90:263', &
      !                        errst=errst)
      !    return
      !end if

      call create(Tensout, Tensin%dl, errst=errst)
      !if(prop_error('copy_tensorc_tensorc: create failed.', &
      !              'Tensors_include.f90:270', errst=errst)) return

      if(present(scalar)) then
          Tensout%elem(:Tensin%dim) = scalar * Tensin%elem(:Tensin%dim)
      else
          Tensout%elem(:Tensin%dim) = Tensin%elem(:Tensin%dim)
      end if

      ! No transformation
      if(.not. present(trans)) return

      ! Check which transformation is applied
      if(trans == 'C') then
          call conj(Tensout, errst)
          !if(prop_error('copy_tensorc_tensorc:'//&
          !              ' conjg failed.', 'Tensors_include.f90:285', &
          !              errst=errst)) return

      elseif(trans == 'T') then
          call transposed(Tensout, errst=errst)
          !if(prop_error('copy_tensorc_tensorc:'//&
          !              ' transpose failed.', 'Tensors_include.f90:291', &
          !              errst=errst)) return

      elseif(trans == 'H') then
          call dagger(Tensout, errst=errst)
          !if(prop_error('copy_tensorc_tensorc:'//&
          !              'dagger failed.', 'Tensors_include.f90:297', &
          !              errst=errst)) return

      elseif(trans /= 'N') then
          !errst = raise_error('copy_tensorc_tensorc:'//&
          !                    ' unknown argument trans.', 4, &
          !                    'Tensors_include.f90:303', errst=errst)
      end if

  end subroutine copy_tensorc_tensorc

Tensors_f90.copy_tensorlist()[source]¶

fortran-subroutine - ?? () Copy a tensor list.

Arguments

ObjoutTYPE(tensorlist), out: Copy the entries of Objin here.
ObjinTYPE(tensorlist), in: source for copy into Dest.

Source Code

show / hide f90 code

Tensors_f90.copy_tensorlistc()[source]¶

fortran-subroutine - ?? () Copy a tensorc list.

Arguments

ObjoutTYPE(tensorlistc), out: Copy the entries of Objin here.
ObjinTYPE(tensorlistc), in: source for copy into Dest.

Source Code

show / hide f90 code

Tensors_f90.copy_tensorlistarray()[source]¶

fortran-subroutine - ?? () Copy an array of tensor lists.

Arguments

ObjoutTYPE(tensorlist)(*), out: Copy the entries of Objin here.
ObjinTYPE(tensorlist)(*), in: source for copy into Objout

Source Code

show / hide f90 code

Tensors_f90.copy_tensorlistarrayc()[source]¶

fortran-subroutine - ?? () Copy an array of tensorc lists.

Arguments

ObjoutTYPE(tensorlistc)(*), out: Copy the entries of Objin here.
ObjinTYPE(tensorlistc)(*), in: source for copy into Objout

Source Code

show / hide f90 code

Tensors_f90.create_tensor()[source]¶

fortran-subroutine - July 2016 (dj) Create a tensor of rank-k.

Arguments

TensTYPE(tensor), out: Allocate an rank-k tensor with certain dimensions.
dlINTEGER, in: Dimension of the vector to be allocated.
initCHARACTER, OPTIONAL, in: Options for initialization of the array. These are initialization with zeros (‘0’), ones (‘1’), no initialization (‘N’) and random numbers (‘R’). Default to ‘N’ (if not present).
mdlINTEGER(*), OPTIONAL, in: Maximal dimension of the tensor during its whole use in the algorithm. Allows to avoid deallocation/allocation steps. Default to dl.

Source Code

show / hide f90 code

Tensors_f90.create_tensorc()[source]¶

fortran-subroutine - July 2016 (dj) Create a tensor of rank-k.

Arguments

TensTYPE(tensorc), out: Allocate an rank-k tensor with certain dimensions.
dlINTEGER, in: Dimension of the vector to be allocated.
initCHARACTER, OPTIONAL, in: Options for initialization of the array. These are initialization with zeros (‘0’), ones (‘1’), no initialization (‘N’) and random numbers (‘R’). Default to ‘N’ (if not present).
mdlINTEGER(*), OPTIONAL, in: Maximal dimension of the tensor during its whole use in the algorithm. Allows to avoid deallocation/allocation steps. Default to dl.

Source Code

show / hide f90 code

Tensors_f90.create_id_tensor()[source]¶

fortran-subroutine - October 2016 (updated dj) Create an identity matrix (or delta function, rank-2 tensor).

Arguments

IdmatTYPE(tensor), out: Create and identity matrix of dimension dim x dim.
TensTYPE(tensor), in: Needed to extract dimension for identity matrix. Has to be rank-3.
sideINTEGER, in: Either 1 or 3 depending if identity matrix should be created as LeftDelta (1, first index) or RightDelta (3, last/third index).

Source Code

show / hide f90 code

Tensors_f90.create_id_tensorc()[source]¶

fortran-subroutine - October 2016 (updated dj) Create an identity matrix (or delta function, rank-2 tensor).

Arguments

IdmatTYPE(tensorc), out: Create and identity matrix of dimension dim x dim.
TensTYPE(tensorc), in: Needed to extract dimension for identity matrix. Has to be rank-3.
sideINTEGER, in: Either 1 or 3 depending if identity matrix should be created as LeftDelta (1, first index) or RightDelta (3, last/third index).

Source Code

show / hide f90 code

Tensors_f90.create_diag_tensor_tensor()[source]¶

fortran-subroutine - June 2018 (dj) Create a rank-2 tensor with the given values on the diagonal.

Arguments

DmatTYPE(tensor), inout: On exit, diagonal rank-2 tensor.
DvalsTYPE(tensor), in: Diagonal entries for the rank-2 tensor as rank-1 tensor.

Source Code

show / hide f90 code

Tensors_f90.create_diag_tensor_tensorc()[source]¶

fortran-subroutine - June 2018 (dj) Create a rank-2 tensor with the given values on the diagonal.

Arguments

DmatTYPE(tensorc), inout: On exit, diagonal rank-2 tensor.
DvalsTYPE(tensor), in: Diagonal entries for the rank-2 tensor as rank-1 tensor.

Source Code

show / hide f90 code

Tensors_f90.create_diag_tensorc_tensorc()[source]¶

fortran-subroutine - June 2018 (dj) Create a rank-2 tensor with the given values on the diagonal.

Arguments

DmatTYPE(tensorc), inout: On exit, diagonal rank-2 tensor.
DvalsTYPE(tensorc), in: Diagonal entries for the rank-2 tensor as rank-1 tensor.

Source Code

show / hide f90 code

Tensors_f90.create_tensorlist()[source]¶

fortran-subroutine - January 2016 (update dj) Create a tensor list of length d1.

Arguments

MatsTYPE(tensorlist), inout: Allocate an array of size d1.
d1INTEGER, in: Length of the matrix list to be allocated.

Source Code

show / hide f90 code

Tensors_f90.create_tensorlistc()[source]¶

fortran-subroutine - January 2016 (update dj) Create a tensorc list of length d1.

Arguments

MatsTYPE(tensorlistc), inout: Allocate an array of size d1.
d1INTEGER, in: Length of the matrix list to be allocated.

Source Code

show / hide f90 code

Tensors_f90.dagger_tensor()[source]¶

fortran-subroutine - October 2016 (dj) Taking complex conjugate followed by transposition of indices or permutation.

Arguments

TensTYPE(tensor), inout: Save a transposition/permutation on the indices of this tensor. Complex conjugated values are taken during this subroutine.
permINTEGER(*), OPTIONAL, in: permutation array has length equal to the rank of the tensor with unique entries 1 to rank. Default to rank, rank - 1, …, 2, 1 (transpose)
dopermLOGICAL, OPTIONAL, in: If true, then permute immediately. If false or not present, permutation is only indicated in the indices.

Details

For details of permutation look into Tensors.f90:transpose_tensor (template defined in Tensors_include.f90)

Source Code

show / hide f90 code

Tensors_f90.destroy_tensor()[source]¶

fortran-subroutine - July 2016 (dj) Destroy a tensor.

Arguments

TensTYPE(tensor), inout: Deallocate the array representing the tensor.

Source Code

show / hide f90 code

Tensors_f90.dagger_tensorc()[source]¶

fortran-subroutine - October 2016 (dj) Taking complex conjugate followed by transposition of indices or permutation.

Arguments

TensTYPE(tensorc), inout: Save a transposition/permutation on the indices of this tensor. Complex conjugated values are taken during this subroutine.
permINTEGER(*), OPTIONAL, in: permutation array has length equal to the rank of the tensor with unique entries 1 to rank. Default to rank, rank - 1, …, 2, 1 (transpose)
dopermLOGICAL, OPTIONAL, in: If true, then permute immediately. If false or not present, permutation is only indicated in the indices.

Details

For details of permutation look into Tensors.f90:transpose_tensorc (template defined in Tensors_include.f90)

Source Code

show / hide f90 code

Tensors_f90.destroy_tensorc()[source]¶

fortran-subroutine - July 2016 (dj) Destroy a tensor.

Arguments

TensTYPE(tensorc), inout: Deallocate the array representing the tensor.

Source Code

show / hide f90 code

Tensors_f90.destroy_tensorlist()[source]¶

fortran-subroutine - January 2016 (update dj) Destroy a list of tensor.

Arguments

MatsTYPE(tensorlist), inout: Deallocate the array of matrixs (including each matrix).

Source Code

show / hide f90 code

Tensors_f90.destroy_tensorlistc()[source]¶

fortran-subroutine - January 2016 (update dj) Destroy a list of tensorc.

Arguments

MatsTYPE(tensorlistc), inout: Deallocate the array of matrixs (including each matrix).

Source Code

show / hide f90 code

Tensors_f90.destroy_imap()[source]¶

fortran-subroutine - September 2017 (dj) Destroy the imap if allocated.

Arguments

ImapperTYPE(imap), inout: Deallocated on exit. It checks if allocated first.

Source Code

show / hide f90 code

Tensors_f90.dot_tensor()[source]¶

fortran-function - October 2016 (dj) Compute dot product <A, B> for tensors.

Arguments

TensaTYPE(tensor), out: First tensor in the dot product (taken with complex conjugated values for complex arrays).
TensbTYPE(tensor), in: Second tensor in the dot product. Has to be the same size as first tensor.

Source Code

show / hide f90 code

Tensors_f90.dot_tensorc()[source]¶

fortran-function - October 2016 (dj) Compute dot product <A, B> for tensors.

Arguments

TensaTYPE(tensorc), out: First tensor in the dot product (taken with complex conjugated values for complex arrays).
TensbTYPE(tensorc), in: Second tensor in the dot product. Has to be the same size as first tensor.

Source Code

show / hide f90 code

Tensors_f90.macdot_real()[source]¶

fortran-function - July 2018 (dj) Dot product implemented to avoid faulty ZDOTC implementation of Mac OS X accelerate package.

Arguments

dimINTEGER, in: Dimension of the dot product.
elemareal(*), in: First argument in dot product. Complex-conjugate taken for complex-valued arguments.
elembreal(*), in: Second argument in dot product.

Details

The interface of the accelerate package to the BLAS routine zdotc appears for various packages, among them scipy as documented in https://github.com/scipy/scipy/issues/1847. Using this workaround, we loose possibly parallel implementations within the dot product.

Source Code

show / hide f90 code

Tensors_f90.macdot_complex()[source]¶

fortran-function - July 2018 (dj) Dot product implemented to avoid faulty ZDOTC implementation of Mac OS X accelerate package.

Arguments

dimINTEGER, in: Dimension of the dot product.
elemacomplex(*), in: First argument in dot product. Complex-conjugate taken for complex-valued arguments.
elembcomplex(*), in: Second argument in dot product.

Details

The interface of the accelerate package to the BLAS routine zdotc appears for various packages, among them scipy as documented in https://github.com/scipy/scipy/issues/1847. Using this workaround, we loose possibly parallel implementations within the dot product.

Source Code

show / hide f90 code

Tensors_f90.equals_tensor_tensor()[source]¶

fortran-function - August 2017 (dj) Compare if two tensors are equal.

Arguments

TensaTYPE(tensor), in: First tensor for comparison.
TensbTYPE(tensor), in: Second tensor for comparison.
tolREAL, OPTIONAL, in: Tolerance for testing the actual entries of the tensor. Default is 1e-14.

Source Code

show / hide f90 code

Tensors_f90.equals_tensorc_tensor()[source]¶

fortran-function - August 2017 (dj) Compare if two tensors are equal.

Arguments

TensaTYPE(tensorc), in: First tensor for comparison.
TensbTYPE(tensor), in: Second tensor for comparison.
tolREAL, OPTIONAL, in: Tolerance for testing the actual entries of the tensor. Default is 1e-14.

Source Code

show / hide f90 code

Tensors_f90.equals_tensor_tensorc()[source]¶

fortran-function - August 2017 (dj) Compare if two tensors are equal.

Arguments

TensaTYPE(tensor), in: First tensor for comparison.
TensbTYPE(tensorc), in: Second tensor for comparison.
tolREAL, OPTIONAL, in: Tolerance for testing the actual entries of the tensor. Default is 1e-14.

Source Code

show / hide f90 code

Tensors_f90.equals_tensorc_tensorc()[source]¶

fortran-function - August 2017 (dj) Compare if two tensors are equal.

Arguments

TensaTYPE(tensorc), in: First tensor for comparison.
TensbTYPE(tensorc), in: Second tensor for comparison.
tolREAL, OPTIONAL, in: Tolerance for testing the actual entries of the tensor. Default is 1e-14.

Source Code

show / hide f90 code

Tensors_f90.expm_real_tensor()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying matrix.

Arguments

TexpTYPE(tensorc), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
screal, in: Additional scalar inside exp-function.
TensTYPE(tensor), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Source Code

show / hide f90 code

Tensors_f90.expm_complex_tensor()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying matrix.

Arguments

TexpTYPE(tensorc), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
sccomplex, in: Additional scalar inside exp-function.
TensTYPE(tensor), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Source Code

show / hide f90 code

Tensors_f90.expm_real_tensorc()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying matrix.

Arguments

TexpTYPE(tensorc), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
screal, in: Additional scalar inside exp-function.
TensTYPE(tensorc), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Source Code

show / hide f90 code

Tensors_f90.expm_complex_tensorc()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying matrix.

Arguments

TexpTYPE(tensorc), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
sccomplex, in: Additional scalar inside exp-function.
TensTYPE(tensorc), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Source Code

show / hide f90 code

Tensors_f90.expm_tensor_real_tensor()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying matrix. This is a dummy.

Arguments

TexpTYPE(tensor), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
screal, in: Additional scalar inside exp-function.
TensTYPE(tensor), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Details

The matrix exponential of a non-hermitian real matrix can be complex and is therefore ill-defined. This methods just raises and error.

Source Code

show / hide f90 code

Tensors_f90.expmh_real_tensor()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying hermitian matrix.

Arguments

TexpTYPE(tensor), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
screal, in: Additional scalar inside exp-function.
TensTYPE(tensor), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Details

Subroutines does not check if matrix is actually hermitian.

Source Code

show / hide f90 code

Tensors_f90.expmh_complex_tensor()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying hermitian matrix.

Arguments

TexpTYPE(tensorc), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
sccomplex, in: Additional scalar inside exp-function.
TensTYPE(tensor), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Details

Subroutines does not check if matrix is actually hermitian.

Source Code

show / hide f90 code

Tensors_f90.expmh_real_tensorc()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying hermitian matrix.

Arguments

TexpTYPE(tensorc), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
screal, in: Additional scalar inside exp-function.
TensTYPE(tensorc), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Details

Subroutines does not check if matrix is actually hermitian.

Source Code

show / hide f90 code

Tensors_f90.expmh_complex_tensorc()[source]¶

fortran-subroutine - August 2017 (dj) Take the exponential of a tensor assuming an underlying hermitian matrix.

Arguments

TexpTYPE(tensorc), out: This is on exit the exponetial. Has rank and dimensions of the input tensor.
sccomplex, in: Additional scalar inside exp-function.
TensTYPE(tensorc), inout: Take the exponential of this tensor.
last_row_idxINTEGER, in: The dimension for the rows are calculated as product(Tens%dl(:last_row_idx)). The remaining indices build the column.

Details

Subroutines does not check if matrix is actually hermitian.

Source Code

show / hide f90 code

Tensors_f90.fuse_tensor()[source]¶

fortran-subroutine - October 2016 (dj) Fuse indices of a tensor together to a single index.

Arguments

TensTYPE(tensor), inout: Merge certain indices of this tensor together to one index.
indINTEGER(*), inout: Contains the positions of the indices to be merged together. Indices must be ascending at this point.

Details

If indices are not neighbors, they are merged into the first position.

Source Code

show / hide f90 code

  subroutine fuse_tensor(Tens, ind, errst)
      type(tensor), intent(inout) :: Tens
      integer, dimension(:), intent(in) :: ind
      integer, intent(out), optional :: errst

      ! Local variables
      ! ---------------

      ! for looping / indexing
      integer :: ii, jj, kk

      ! old rank
      integer :: orank

      ! copy of dimensions / permutations
      integer, dimension(:), pointer :: darr

      ! Permutation to group merged indices together
      integer, dimension(Tens%rank) :: perm

      !if(present(errst)) errst = 0

      !if(maxval(ind) > Tens%rank) then
      !    errst = raise_error('fuse_tensor: index exceeds '// &
      !                        'rank.', 2, 'Tensors_include.f90:1299', errst=errst)
      !    return
      !end if

      !if(any(ind(2:) - ind(:size(ind) - 1) < 0)) then
      !    errst = raise_error('fuse_tensor: indices not '// &
      !                        'ascending.', 5, 'Tensors_include.f90:1305', errst=errst)
      !    return
      !end if

      ! Permute first to avoid unravelling this
      call permute(Tens, errst=errst)
      !if(prop_error('fuse_tensor: permute (1) failed,', &
      !              'Tensors_include.f90:1312', errst=errst)) return

      perm = [(ii, ii = 1, Tens%rank)]
      do ii = 2, size(ind)
          perm(ind(1) + ii - 1) = ind(ii)
      end do

      kk = ind(1) + size(ind)
      do ii = 1, size(ind) - 1
          do jj = ind(ii) + 1, ind(ii + 1) - 1
              perm(kk) = jj
              kk = kk + 1
          end do
      end do

      do jj = ind(size(ind)) + 1, Tens%rank
          perm(kk) = jj
          kk = kk + 1
      end do

      Tens%idx = perm
      call permute(Tens, errst=errst)
      !if(prop_error('fuse_tensor: permute (2) failed,', &
      !              'Tensors_include.f90:1335', errst=errst)) return

      allocate(darr(Tens%rank))
      darr = Tens%dl

      orank = Tens%rank
      Tens%rank = Tens%rank - size(ind) + 1
      deallocate(Tens%dl, Tens%idx, Tens%mdl)
      allocate(Tens%dl(Tens%rank), Tens%idx(Tens%rank), Tens%mdl(Tens%rank))
      Tens%idx = [(ii, ii = 1, Tens%rank)]

      ! Reset dimensions
      Tens%dl(1:ind(1) - 1) = darr(1:ind(1) - 1)
      Tens%dl(ind(1)) = product(darr(ind(1):ind(1) + size(ind) - 1))
      Tens%dl(ind(1) + 1:Tens%rank) = darr(ind(1) + size(ind):orank)

      ! Temporary solution, not really true
      Tens%mdl = Tens%dl

      deallocate(darr)

  end subroutine fuse_tensor

Tensors_f90.fuse_tensorc()[source]¶

fortran-subroutine - October 2016 (dj) Fuse indices of a tensor together to a single index.

Arguments

TensTYPE(tensorc), inout: Merge certain indices of this tensor together to one index.
indINTEGER(*), inout: Contains the positions of the indices to be merged together. Indices must be ascending at this point.

Details

If indices are not neighbors, they are merged into the first position.

Source Code

show / hide f90 code

  subroutine fuse_tensorc(Tens, ind, errst)
      type(tensorc), intent(inout) :: Tens
      integer, dimension(:), intent(in) :: ind
      integer, intent(out), optional :: errst

      ! Local variables
      ! ---------------

      ! for looping / indexing
      integer :: ii, jj, kk

      ! old rank
      integer :: orank

      ! copy of dimensions / permutations
      integer, dimension(:), pointer :: darr

      ! Permutation to group merged indices together
      integer, dimension(Tens%rank) :: perm

      !if(present(errst)) errst = 0

      !if(maxval(ind) > Tens%rank) then
      !    errst = raise_error('fuse_tensorc: index exceeds '// &
      !                        'rank.', 2, 'Tensors_include.f90:1299', errst=errst)
      !    return
      !end if

      !if(any(ind(2:) - ind(:size(ind) - 1) < 0)) then
      !    errst = raise_error('fuse_tensorc: indices not '// &
      !                        'ascending.', 5, 'Tensors_include.f90:1305', errst=errst)
      !    return
      !end if

      ! Permute first to avoid unravelling this
      call permute(Tens, errst=errst)
      !if(prop_error('fuse_tensorc: permute (1) failed,', &
      !              'Tensors_include.f90:1312', errst=errst)) return

      perm = [(ii, ii = 1, Tens%rank)]
      do ii = 2, size(ind)
          perm(ind(1) + ii - 1) = ind(ii)
      end do

      kk = ind(1) + size(ind)
      do ii = 1, size(ind) - 1
          do jj = ind(ii) + 1, ind(ii + 1) - 1
              perm(kk) = jj
              kk = kk + 1
          end do
      end do

      do jj = ind(size(ind)) + 1, Tens%rank
          perm(kk) = jj
          kk = kk + 1
      end do

      Tens%idx = perm
      call permute(Tens, errst=errst)
      !if(prop_error('fuse_tensorc: permute (2) failed,', &
      !              'Tensors_include.f90:1335', errst=errst)) return

      allocate(darr(Tens%rank))
      darr = Tens%dl

      orank = Tens%rank
      Tens%rank = Tens%rank - size(ind) + 1
      deallocate(Tens%dl, Tens%idx, Tens%mdl)
      allocate(Tens%dl(Tens%rank), Tens%idx(Tens%rank), Tens%mdl(Tens%rank))
      Tens%idx = [(ii, ii = 1, Tens%rank)]

      ! Reset dimensions
      Tens%dl(1:ind(1) - 1) = darr(1:ind(1) - 1)
      Tens%dl(ind(1)) = product(darr(ind(1):ind(1) + size(ind) - 1))
      Tens%dl(ind(1) + 1:Tens%rank) = darr(ind(1) + size(ind):orank)

      ! Temporary solution, not really true
      Tens%mdl = Tens%dl

      deallocate(darr)

  end subroutine fuse_tensorc

Tensors_f90.fuse_all_tensor()[source]¶

fortran-subroutine - October 2017 (dj) Fuse equally sized subsets of links containing in total all links.

Arguments

TensTYPE(tensor), inout: Fuse links in this tensor.
idxINTEGER(*, *), in: Each column contain the links to be fused. The number of rows times the number of columns must correspond to the rank of the tensor. ii-th column is ii-th new index.
methodCHARACTER, in: Dummy flag to comply with the interface for the symmetric tensors.
orderedLOGICAL, OPTIONAL, in: If flag is true, the permutation of the indices does not have to be executed. Default to false (permute links).

Source Code

show / hide f90 code

  subroutine fuse_all_tensor(Tens, idx, method, ordered, errst)
      type(tensor), intent(inout) :: Tens
      integer, dimension(:, :), intent(in) :: idx
      character, intent(in) :: method
      logical, intent(in), optional :: ordered
      integer, intent(out), optional :: errst

      ! Local variables
      ! ---------------

      ! for looping
      integer :: ii

      ! for indexing while looping
      integer :: i1, i2

      ! duplette for optional argument
      logical :: ordered_

      ! permutation to put fused indices next to each other
      integer, dimension(:), allocatable :: perm

      ! new dimension of the tensor
      integer, dimension(:), allocatable :: newdl

      ! Avoid unused variable message for intentionally unused variables
      !if(.false.) print *, method

      !if(present(errst)) errst = 0

      !if(size(idx) /= Tens%rank) then
      !   errst = raise_error('fuse_all_tensor : rank mismatch.', &
      !                       99, 'Tensors_include.f90:1430', errst=errst)
      !   return
      !end if

      ordered_ = .false.
      if(present(ordered)) ordered_ = ordered

      if(.not. ordered_) then
          allocate(perm(size(idx)))
          perm = reshape(idx, [size(idx)])

          call transposed(Tens, perm, doperm=.true.)

          deallocate(perm)
      end if

      Tens%rank = size(idx, 2)
      allocate(newdl(Tens%rank))

      i1 = 1
      i2 = size(idx, 1)

      do ii = 1, Tens%rank
          newdl(ii) = product(Tens%dl(i1:i2))
          i1 = i1 + size(idx, 1)
          i2 = i2 + size(idx, 1)
      end do

      deallocate(Tens%dl, Tens%idx)
      allocate(Tens%dl(Tens%rank), Tens%idx(Tens%rank))

      Tens%dl = newdl
      Tens%idx = [(ii, ii = 1, Tens%rank)]

      ! Figure out maximal dimension

      i1 = 1
      i2 = size(idx, 1)

      do ii = 1, Tens%rank
          newdl(ii) = product(Tens%mdl(i1:i2))
          i1 = i1 + size(idx, 1)
          i2 = i2 + size(idx, 1)
      end do

      deallocate(Tens%mdl)
      allocate(Tens%mdl(Tens%rank))

      Tens%mdl = newdl

      deallocate(newdl)

  end subroutine fuse_all_tensor

Tensors_f90.fuse_all_tensorc()[source]¶

fortran-subroutine - October 2017 (dj) Fuse equally sized subsets of links containing in total all links.

Arguments

TensTYPE(tensorc), inout: Fuse links in this tensor.
idxINTEGER(*, *), in: Each column contain the links to be fused. The number of rows times the number of columns must correspond to the rank of the tensor. ii-th column is ii-th new index.
methodCHARACTER, in: Dummy flag to comply with the interface for the symmetric tensors.
orderedLOGICAL, OPTIONAL, in: If flag is true, the permutation of the indices does not have to be executed. Default to false (permute links).

Source Code

show / hide f90 code

  subroutine fuse_all_tensorc(Tens, idx, method, ordered, errst)
      type(tensorc), intent(inout) :: Tens
      integer, dimension(:, :), intent(in) :: idx
      character, intent(in) :: method
      logical, intent(in), optional :: ordered
      integer, intent(out), optional :: errst

      ! Local variables
      ! ---------------

      ! for looping
      integer :: ii

      ! for indexing while looping
      integer :: i1, i2

      ! duplette for optional argument
      logical :: ordered_

      ! permutation to put fused indices next to each other
      integer, dimension(:), allocatable :: perm

      ! new dimension of the tensor
      integer, dimension(:), allocatable :: newdl

      ! Avoid unused variable message for intentionally unused variables
      !if(.false.) print *, method

      !if(present(errst)) errst = 0

      !if(size(idx) /= Tens%rank) then
      !   errst = raise_error('fuse_all_tensorc : rank mismatch.', &
      !                       99, 'Tensors_include.f90:1430', errst=errst)
      !   return
      !end if

      ordered_ = .false.
      if(present(ordered)) ordered_ = ordered

      if(.not. ordered_) then
          allocate(perm(size(idx)))
          perm = reshape(idx, [size(idx)])

          call transposed(Tens, perm, doperm=.true.)

          deallocate(perm)
      end if

      Tens%rank = size(idx, 2)
      allocate(newdl(Tens%rank))

      i1 = 1
      i2 = size(idx, 1)

      do ii = 1, Tens%rank
          newdl(ii) = product(Tens%dl(i1:i2))
          i1 = i1 + size(idx, 1)
          i2 = i2 + size(idx, 1)
      end do

      deallocate(Tens%dl, Tens%idx)
      allocate(Tens%dl(Tens%rank), Tens%idx(Tens%rank))

      Tens%dl = newdl
      Tens%idx = [(ii, ii = 1, Tens%rank)]

      ! Figure out maximal dimension

      i1 = 1
      i2 = size(idx, 1)

      do ii = 1, Tens%rank
          newdl(ii) = product(Tens%mdl(i1:i2))
          i1 = i1 + size(idx, 1)
          i2 = i2 + size(idx, 1)
      end do

      deallocate(Tens%mdl)
      allocate(Tens%mdl(Tens%rank))

      Tens%mdl = newdl

      deallocate(newdl)

  end subroutine fuse_all_tensorc

Tensors_f90.gaxpy_tensor_real_tensor()[source]¶

fortran-subroutine - March 2016 (updated dj) Y = Y + a * X for real a

Arguments

YyTYPE(tensor), inout: On entry, tensor. On exit tensor times scalar added to this tensor,
screal, in: Scalar multiplied with tensor X.
XxTYPE(tensor), inout: Tensor added to tensor Y. Is scaled with constant sc.

Source Code

show / hide f90 code

Tensors_f90.gaxpy_tensorc_complex_tensorc()[source]¶

fortran-subroutine - March 2016 (updated dj) Y = Y + a * X for complex a

Arguments

YyTYPE(tensorc), inout: On entry, tensor. On exit tensor times scalar added to this tensor,
sccomplex, in: Scalar multiplied with tensor X.
XxTYPE(tensorc), inout: Tensor added to tensor Y. Is scaled with constant sc.

Source Code

show / hide f90 code

Tensors_f90.gaxpy_tensorc_real_tensor()[source]¶

fortran-subroutine - March 2016 (updated dj) Y = Y + a * X for real a

Arguments

YyTYPE(tensorc), inout: On entry, tensor. On exit tensor times scalar added to this tensor,
screal, in: Scalar multiplied with tensor X.
XxTYPE(tensor), inout: Tensor added to tensor Y. Is scaled with constant sc.

Source Code

show / hide f90 code

Tensors_f90.gaxpy_tensorc_complex_tensor()[source]¶

fortran-subroutine - March 2016 (updated dj) Y = Y + a * X for complex a

Arguments

YyTYPE(tensorc), inout: On entry, tensor. On exit tensor times scalar added to this tensor,
sccomplex, in: Scalar multiplied with tensor X.
XxTYPE(tensor), inout: Tensor added to tensor Y. Is scaled with constant sc.

Source Code

show / hide f90 code

Tensors_f90.gaxpy_tensorc_real_tensorc()[source]¶

fortran-subroutine - March 2016 (updated dj) Y = Y + a * X for real a

Arguments

YyTYPE(tensorc), inout: On entry, tensor. On exit tensor times scalar added to this tensor,
screal, in: Scalar multiplied with tensor X.
XxTYPE(tensorc), inout: Tensor added to tensor Y. Is scaled with constant sc.

Source Code

show / hide f90 code

Tensors_f90.get_scalar_tensor()[source]¶

fortran-function - July 2017 (dj) Get the scalar if the tensor represents a rank-0 tensor.

Arguments

QtensTYPE(Qtensor), in: Return the scalar entry of a rank-0 tensor.

Source Code

show / hide f90 code

Tensors_f90.get_scalar_tensorc()[source]¶

fortran-function - July 2017 (dj) Get the scalar if the tensor represents a rank-0 tensor.

Arguments

QtensTYPE(Qtensorc), in: Return the scalar entry of a rank-0 tensor.

Source Code

show / hide f90 code

Tensors_f90.has_nan_tensor()[source]¶

fortran-function - October 2017 (dj) Check if the tensor has NAN in the actual array.

Arguments

TensTYPE(tensor), in: Check NAN on the entries of this tensor. Check does not apply to rank, dimensions, etc.

Source Code

show / hide f90 code

Tensors_f90.has_nan_tensorc()[source]¶

fortran-function - October 2017 (dj) Check if the tensor has NAN in the actual array.

Arguments

TensTYPE(tensorc), in: Check NAN on the entries of this tensor. Check does not apply to rank, dimensions, etc.

Source Code

show / hide f90 code

Tensors_f90.is_eye_tensor()[source]¶

fortran-function - August 2017 (dj) Check if the tensor is an identity.

Arguments

TensTYPE(tensor), in: This tensor is checked if it is an identity.

Details

We define the identity for any rank as a tensor with ones for i_1 = i_2 = … = i_n, and otherwise zeros.

Source Code

show / hide f90 code

Tensors_f90.is_eye_tensorc()[source]¶

fortran-function - August 2017 (dj) Check if the tensor is an identity.

Arguments

TensTYPE(tensorc), in: This tensor is checked if it is an identity.

Details

We define the identity for any rank as a tensor with ones for i_1 = i_2 = … = i_n, and otherwise zeros.

Source Code

show / hide f90 code

Tensors_f90.is_set_tensor()[source]¶

fortran-function - August 2017 (dj) Check if a tensor is in use.

Arguments

TensTYPE(tensor), in: Check if the tensor was used, i.e. a call to create. The check is on the rank of the tensor.

Source Code

show / hide f90 code

Tensors_f90.is_set_tensorc()[source]¶

fortran-function - August 2017 (dj) Check if a tensor is in use.

Arguments

TensTYPE(tensorc), in: Check if the tensor was used, i.e. a call to create. The check is on the rank of the tensor.

Source Code

show / hide f90 code

Tensors_f90.kron_tensor_tensor()[source]¶

fortran-subroutine - May 2017 (dj) Kronecker product bipartions on two tensors.

Arguments

ToutTYPE(tensor), inout: Storing the result of the Kronecker product.
TlTYPE(tensor), inout: Left tensor in the Kronecker product.
TrTYPE(tensor), inout: Right tensor in the Kronecker product.
llrINTEGER, in: Last index contributing to the rows, all over 1:llr. This is for the left tensor Tl.
lrrINTEGER, in: Last index contributing to the rows, all over 1:lrr. This is for the left tensor Tr.
translCHARACTER, in: Defines the transformation executed on the left matrix 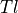$Tl$ when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed), or ‘D’ (dagger / conjugate transposed).
transrCHARACTER, in: Defines the transformation executed on the left matrix 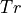$Tr$ when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed), or ‘D’ (dagger / conjugate transposed).
opCHARACTER, in: Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.

Details

The output is always a rank-4 tensor. The intended use is for rank-2 tensors.

Source Code

show / hide f90 code

Tensors_f90.kron_tensorc_tensorc()[source]¶

fortran-subroutine - May 2017 (dj) Kronecker product bipartions on two tensors.

Arguments

ToutTYPE(tensorc), inout: Storing the result of the Kronecker product.
TlTYPE(tensorc), inout: Left tensor in the Kronecker product.
TrTYPE(tensorc), inout: Right tensor in the Kronecker product.
llrINTEGER, in: Last index contributing to the rows, all over 1:llr. This is for the left tensor Tl.
lrrINTEGER, in: Last index contributing to the rows, all over 1:lrr. This is for the left tensor Tr.
translCHARACTER, in: Defines the transformation executed on the left matrix $Tl$ when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed), or ‘D’ (dagger / conjugate transposed).
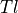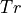transrCHARACTER, in: Defines the transformation executed on the left matrix $Tr$ when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed), or ‘D’ (dagger / conjugate transposed).
opCHARACTER, in: Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.

Details

The output is always a rank-4 tensor. The intended use is for rank-2 tensors.

Source Code

show / hide f90 code

Tensors_f90.kron_tensorc_tensor()[source]¶

fortran-subroutine - May 2017 (dj) Kronecker product bipartions on two tensors.

Arguments

ToutTYPE(tensorc), inout: Storing the result of the Kronecker product.
TlTYPE(tensor), inout: Left tensor in the Kronecker product.
TrTYPE(tensor), inout: Right tensor in the Kronecker product.
llrINTEGER, in: Last index contributing to the rows, all over 1:llr. This is for the left tensor Tl.
lrrINTEGER, in: Last index contributing to the rows, all over 1:lrr. This is for the left tensor Tr.
translCHARACTER, in: Defines the transformation executed on the left matrix $Tl$ when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed), or ‘D’ (dagger / conjugate transposed).
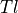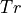transrCHARACTER, in: Defines the transformation executed on the left matrix $Tr$ when taking the tensor product. Either ‘N’ (none), ‘T’ (transposed), or ‘D’ (dagger / conjugate transposed).
opCHARACTER, in: Either ‘N’ for usual Kronecker product, or ‘+’ for adding to the result.

Details

The output is always a rank-4 tensor. The intended use is for rank-2 tensors.

Source Code

show / hide f90 code

Tensors_f90.maxlineardim_tensor()[source]¶

fortran-function - June 2017 (updated dj) Return the maximal dimension of all n indices in the rank-n tensor, or selected indices.

Arguments

TensTYPE(tensor), in: Get the maximal dimension of this tensor.
idxINTEGER(*), in: Search only over these indices of the rank-n tensor.

Source Code

show / hide f90 code

Tensors_f90.maxlineardim_tensorc()[source]¶

fortran-function - June 2017 (updated dj) Return the maximal dimension of all n indices in the rank-n tensor, or selected indices.

Arguments

TensTYPE(tensorc), in: Get the maximal dimension of this tensor.
idxINTEGER(*), in: Search only over these indices of the rank-n tensor.

Source Code

show / hide f90 code

Tensors_f90.maxvalue_tensor()[source]¶

fortran-function - June 2017 (dj) Return the maximal value of all entries in the tensor.

Arguments

TensTYPE(tensor), in: Get the maximal entry of this tensor. For complex tensors, the absolute value is considered.

Source Code

show / hide f90 code

Tensors_f90.maxvalue_tensorc()[source]¶

fortran-function - June 2017 (dj) Return the maximal value of all entries in the tensor.

Arguments

TensTYPE(tensorc), in: Get the maximal entry of this tensor. For complex tensors, the absolute value is considered.

Source Code

show / hide f90 code

Tensors_f90.norm_tensor()[source]¶

fortran-function - October 2016 (update dj) Compute <A, A> for a tensor.

Arguments

TensTYPE(tensor), in: Get norm of this tensor <A, A>.

Source Code

show / hide f90 code

Tensors_f90.norm_tensorc()[source]¶

fortran-function - October 2016 (update dj) Compute <A, A> for a tensor.

Arguments

TensTYPE(tensorc), in: Get norm of this tensor <A, A>.

Source Code

show / hide f90 code

Tensors_f90.permute_tensor()[source]¶

fortran-subroutine - July 2016 (dj) Bring the tensor in the actual order defined in idx in the memory. It is “COME FROM” indexing.

Arguments

TensTYPE(tensor), inout: Permute the indices of this tensor into the order stored in idx.

Details

We divide the indices into three blocks (A, B, C), where the first and the last block contains indices not changing their position.

Source Code

show / hide f90 code

  subroutine permute_tensor(Tens, errst)
      type(tensor), intent(inout) :: Tens
      integer, intent(out), optional :: errst

      ! Local variables
      ! ---------------

      ! for looping
      integer :: ii, jj, kk

      ! index in new array
      integer :: idx

      ! number of indices in each block (A, B, C)
      integer :: na, nb, nc

      ! total dimension of indices in each block (A, B, C)
      integer :: da, db, dc

      ! product of da * db
      integer :: dab

      ! pos in old and new array
      integer, dimension(:), pointer :: posold, newdim, cumdim

      ! temporary memory
      real(KIND=rKIND), dimension(:), pointer :: pelem

      !if(present(errst)) errst = 0

      !if(size(Tens%idx, 1) > Tens%rank) then
      !    errst = raise_error('permute_tensor: dimension '// &
      !                        'mismatch.', 99, 'Tensors_include.f90:2005', errst=errst)
      !    return
      !end if

      ! Find indices in block A
      na = 0
      da = 1
      do ii = 1, Tens%rank
          if(ii == Tens%idx(ii)) then
              na = na + 1
              da = da * Tens%dl(ii)
          else
              exit
          end if
      end do

      ! If block size is dim - no permutation
      if(na == Tens%rank) return

      allocate(pelem(size(Tens%elem, 1)))

      ! Find indices in block C
      nc = 0
      dc = 1
      do ii = Tens%rank, 1, -1
          if(ii == Tens%idx(ii)) then
              nc = nc + 1
              dc = dc * Tens%dl(ii)
          else
              exit
          end if
      end do

      ! Set block B
      nb = Tens%rank - na - nc
      db = 1
      do ii = 1, nb
          db = db * Tens%dl(na + ii)
      end do

      ! Set dimension in block B after permutation
      allocate(cumdim(nb), newdim(nb))

      newdim(1) = da
      do ii = na + 1, na + nb - 1
          newdim(ii - na + 1) = newdim(ii - na) * Tens%dl(Tens%idx(ii))
      end do

      do ii = na + 1, na + nb
          cumdim(Tens%idx(ii) - na) = newdim(ii - na)
      end do

      ! Arrays for old position
      allocate(posold(nb))
      posold = 0
      posold(1) = -1

      ! Loop over indices to be permuted
      ! --------------------------------

      if((na /= 0) .and. (nc /= 0)) then
          ! Unchagend indices in front and back

          dab = da * db

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1
              kk = 0

              do jj = 1, dc
                  pelem(idx:idx + da - 1) = &
                       Tens%elem(kk + da * (ii - 1) + 1:kk + da * ii)
                  idx = idx + dab
                  kk = kk + dab
              end do
          end do

      elseif(na /= 0) then
          ! Unchanged indices in front

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1

              pelem(idx:idx + da - 1) = Tens%elem(da * (ii - 1) + 1:da * ii)
          end do

      elseif(nc /= 0) then
          ! Unchanged indices in back

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1
              kk = ii

              do jj = 1, dc
                  pelem(idx) = Tens%elem(kk)
                  idx = idx + db
                  kk = kk + db
              end do
          end do

      else
          ! No unchanged indices in front or back

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1

              pelem(idx) = Tens%elem(ii)
          end do
      end if

      deallocate(Tens%elem)
      Tens%elem => pelem
      pelem => null()
      !Tens%elem(:Tens%dim) = pelem
      Tens%dl = Tens%dl(Tens%idx)
      Tens%idx = [(ii, ii = 1, Tens%rank)]

      deallocate(newdim, posold, cumdim)
      !deallocate(pelem, newdim, posold, cumdim)

  end subroutine permute_tensor

Tensors_f90.permute_tensorc()[source]¶

fortran-subroutine - July 2016 (dj) Bring the tensor in the actual order defined in idx in the memory. It is “COME FROM” indexing.

Arguments

TensTYPE(tensorc), inout: Permute the indices of this tensor into the order stored in idx.

Details

We divide the indices into three blocks (A, B, C), where the first and the last block contains indices not changing their position.

Source Code

show / hide f90 code

  subroutine permute_tensorc(Tens, errst)
      type(tensorc), intent(inout) :: Tens
      integer, intent(out), optional :: errst

      ! Local variables
      ! ---------------

      ! for looping
      integer :: ii, jj, kk

      ! index in new array
      integer :: idx

      ! number of indices in each block (A, B, C)
      integer :: na, nb, nc

      ! total dimension of indices in each block (A, B, C)
      integer :: da, db, dc

      ! product of da * db
      integer :: dab

      ! pos in old and new array
      integer, dimension(:), pointer :: posold, newdim, cumdim

      ! temporary memory
      complex(KIND=rKIND), dimension(:), pointer :: pelem

      !if(present(errst)) errst = 0

      !if(size(Tens%idx, 1) > Tens%rank) then
      !    errst = raise_error('permute_tensorc: dimension '// &
      !                        'mismatch.', 99, 'Tensors_include.f90:2005', errst=errst)
      !    return
      !end if

      ! Find indices in block A
      na = 0
      da = 1
      do ii = 1, Tens%rank
          if(ii == Tens%idx(ii)) then
              na = na + 1
              da = da * Tens%dl(ii)
          else
              exit
          end if
      end do

      ! If block size is dim - no permutation
      if(na == Tens%rank) return

      allocate(pelem(size(Tens%elem, 1)))

      ! Find indices in block C
      nc = 0
      dc = 1
      do ii = Tens%rank, 1, -1
          if(ii == Tens%idx(ii)) then
              nc = nc + 1
              dc = dc * Tens%dl(ii)
          else
              exit
          end if
      end do

      ! Set block B
      nb = Tens%rank - na - nc
      db = 1
      do ii = 1, nb
          db = db * Tens%dl(na + ii)
      end do

      ! Set dimension in block B after permutation
      allocate(cumdim(nb), newdim(nb))

      newdim(1) = da
      do ii = na + 1, na + nb - 1
          newdim(ii - na + 1) = newdim(ii - na) * Tens%dl(Tens%idx(ii))
      end do

      do ii = na + 1, na + nb
          cumdim(Tens%idx(ii) - na) = newdim(ii - na)
      end do

      ! Arrays for old position
      allocate(posold(nb))
      posold = 0
      posold(1) = -1

      ! Loop over indices to be permuted
      ! --------------------------------

      if((na /= 0) .and. (nc /= 0)) then
          ! Unchagend indices in front and back

          dab = da * db

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1
              kk = 0

              do jj = 1, dc
                  pelem(idx:idx + da - 1) = &
                       Tens%elem(kk + da * (ii - 1) + 1:kk + da * ii)
                  idx = idx + dab
                  kk = kk + dab
              end do
          end do

      elseif(na /= 0) then
          ! Unchanged indices in front

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1

              pelem(idx:idx + da - 1) = Tens%elem(da * (ii - 1) + 1:da * ii)
          end do

      elseif(nc /= 0) then
          ! Unchanged indices in back

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1
              kk = ii

              do jj = 1, dc
                  pelem(idx) = Tens%elem(kk)
                  idx = idx + db
                  kk = kk + db
              end do
          end do

      else
          ! No unchanged indices in front or back

          do ii = 1, db
              posold(1) = posold(1) + 1

              ! Increment if ..
              jj = 1
              do while(posold(jj) >= Tens%dl(na + jj))
                  posold(jj) = 0
                  posold(jj + 1) = posold(jj + 1) + 1
                  jj = jj + 1
              end do

              ! Position in the permuted array
              idx = sum(posold * cumdim) + 1

              pelem(idx) = Tens%elem(ii)
          end do
      end if

      deallocate(Tens%elem)
      Tens%elem => pelem
      pelem => null()
      !Tens%elem(:Tens%dim) = pelem
      Tens%dl = Tens%dl(Tens%idx)
      Tens%idx = [(ii, ii = 1, Tens%rank)]

      deallocate(newdim, posold, cumdim)
      !deallocate(pelem, newdim, posold, cumdim)

  end subroutine permute_tensorc

Tensors_f90.perturb_tensor()[source]¶

fortran-subroutine - December 2018 (dj) Perturb a tensor by a some small epsilon, entry-by-entry.

Arguments

TensTYPE(tensor), inout: Tensor to be perturbed.
epsilonreal, OPTIONAL, in: Scale a randomized tensor by epsilon and add to original tensor. Default to 1e-8

Source Code

show / hide f90 code

Tensors_f90.perturb_tensorc()[source]¶

fortran-subroutine - December 2018 (dj) Perturb a tensor by a some small epsilon, entry-by-entry.

Arguments

TensTYPE(tensorc), inout: Tensor to be perturbed.
epsilonreal, OPTIONAL, in: Scale a randomized tensor by epsilon and add to original tensor. Default to 1e-8

Source Code

show / hide f90 code

Tensors_f90.pointto_tensor()[source]¶

fortran-subroutine - March 2018 (dj) Copy Objb to Obja by setting the pointers and nullify Objb.

Arguments

ObjaTYPE(tensor), inout: On exit, it contains the same information as Objb
ObjbTYPE(tensor), inout: Empty on exit.

Source Code

show / hide f90 code

Tensors_f90.pointto_tensorc()[source]¶

fortran-subroutine - March 2018 (dj) Copy Objb to Obja by setting the pointers and nullify Objb.

Arguments

ObjaTYPE(tensorc), inout: On exit, it contains the same information as Objb
ObjbTYPE(tensorc), inout: Empty on exit.

Source Code

show / hide f90 code

Tensors_f90.pointto_tensorc_tensor()[source]¶

fortran-subroutine - March 2018 (dj) Copy Objb to Obja by setting the pointers and nullify Objb. Conversion from real to complex is without pointers.

Arguments

ObjaTYPE(tensorc), inout: On exit, it contains the same information as Objb
ObjbTYPE(tensor), inout: Empty on exit.

Source Code

show / hide f90 code

Tensors_f90.print_tensor()[source]¶

fortran-subroutine - March 2016 (updated dj) Tensor print.

Arguments

ObjTYPE(tensor), in: Deprecated subroutines. Uses write_tensor internally.

Source Code

show / hide f90 code

Tensors_f90.print_tensorc()[source]¶

fortran-subroutine - March 2016 (updated dj) Tensor print.

Arguments

ObjTYPE(tensorc), in: Deprecated subroutines. Uses write_tensorc internally.

Source Code

show / hide f90 code

Tensors_f90.project_tensor()[source]¶

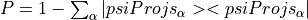
fortran-subroutine - March 2016 (updated dj) Apply the projector P to Aa and store in Bb, where P is defined as $P = 1 - \sum_{\alpha} | psiProjs_{\alpha}> <psiProjs_{\alpha}|$

Arguments

BbTYPE(tensor), out: Store projection of A in this tensor.
AaTYPE(tensor), in: Get projection of this tensor.
PsiProjsTYPE(tensor)(*), in: Array of tensors defining the projector.

Details

Used in orthogonalizing an MPS against another set of MPSs.

Source Code

show / hide f90 code

Tensors_f90.project_tensorc()[source]¶

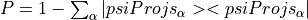
fortran-subroutine - March 2016 (updated dj) Apply the projector P to Aa and store in Bb, where P is defined as $P = 1 - \sum_{\alpha} | psiProjs_{\alpha}> <psiProjs_{\alpha}|$

Arguments

BbTYPE(tensorc), out: Store projection of A in this tensor.
AaTYPE(tensorc), in: Get projection of this tensor.
PsiProjsTYPE(tensorc)(*), in: Array of tensors defining the projector.

Details

Used in orthogonalizing an MPS against another set of MPSs.

Source Code

show / hide f90 code

Tensors_f90.qmattomat_tensor()[source]¶

fortran-subroutine - ?? (dj) Dummy interface resulting in a copy.

Arguments

ToutTYPE(tensor), inout: Copy of input tensor.
TinTYPE(tensor), in: Copy this tensor, which is already a tensor without symmetries.
ImapperTYPE(IMAP), in: Mapping quantum numbers to matrix. Unused.

Source Code

show / hide f90 code

Tensors_f90.qmattomat_tensorc()[source]¶

fortran-subroutine - ?? (dj) Dummy interface resulting in a copy.

Arguments

ToutTYPE(tensorc), inout: Copy of input tensor.
TinTYPE(tensorc), in: Copy this tensor, which is already a tensor without symmetries.
ImapperTYPE(IMAP), in: Mapping quantum numbers to matrix. Unused.

Source Code

show / hide f90 code

Tensors_f90.randomize_tensor()[source]¶

fortran-subroutine - Randomize the elements of the tensor. March 2016 (updated dj)

Arguments

TensTYPE(tensor), inout: Randomize entries between [-1, 1] (real array) or [-1-i, 1+i] (complex arrays).

Source Code

show / hide f90 code

Tensors_f90.randomize_tensorc()[source]¶

fortran-subroutine - Randomize the elements of the tensor. March 2016 (updated dj)

Arguments

TensTYPE(tensorc), inout: Randomize entries between [-1, 1] (real array) or [-1-i, 1+i] (complex arrays).

Source Code

show / hide f90 code

Tensors_f90.rank_tensor()[source]¶

fortran-function - June 2017 (dj) Return the rank of a tensor.

Arguments

TensTYPE(tensor), in: Return the rank of the tensor.

Source Code

show / hide f90 code

Tensors_f90.rank_tensorc()[source]¶

fortran-function - June 2017 (dj) Return the rank of a tensor.

Arguments

TensTYPE(tensorc), in: Return the rank of the tensor.

Source Code

show / hide f90 code

Tensors_f90.read_tensor()[source]¶

fortran-subroutine - August 2015 (dj) Read an tensor from a given unit.

Arguments

TensTYPE(tensor), out: will be read from given destination.
unitINTEGER, in: read from this unit
formCHARACTER, in: ‘H’ (human readable), ‘B’ (binary).

Details

For a detailed description go to the documentation of the corresponding write method write_tensor.

Source Code

show / hide f90 code

Tensors_f90.read_tensorc()[source]¶

fortran-subroutine - August 2015 (dj) Read an tensor from a given unit.

Arguments

TensTYPE(tensorc), out: will be read from given destination.
unitINTEGER, in: read from this unit
formCHARACTER, in: ‘H’ (human readable), ‘B’ (binary).

Details

For a detailed description go to the documentation of the corresponding write method write_tensorc.

Source Code

show / hide f90 code

Tensors_f90.scale_tensor_real()[source]¶

fortran-subroutine - March 2016 (updated dj) Scale a tensor by a scalar.

Arguments

scREALSCALAR, in: Scalar to be multiplied with tensor.
ObjTYPE(COMPLEXtensor), inout: Tensor to be scaled with scalar.

Source Code

show / hide f90 code

Tensors_f90.scale_tensorc_complex()[source]¶

fortran-subroutine - March 2016 (updated dj) Scale a tensor by a scalar.

Arguments

scREALSCALAR, in: Scalar to be multiplied with tensor.
ObjTYPE(COMPLEXtensorc), inout: Tensor to be scaled with scalar.

Source Code

show / hide f90 code

Tensors_f90.scale_tensorc_real()[source]¶

fortran-subroutine - March 2016 (updated dj) Scale a tensor by a scalar.

Arguments

scREALSCALAR, in: Scalar to be multiplied with tensor.
ObjTYPE(COMPLEXtensorc), inout: Tensor to be scaled with scalar.

Source Code

show / hide f90 code

Tensors_f90.set_hash_tensor()[source]¶

fortran-subroutine - October 2016 (dj) Dummy subroutine to comply with interface in qTensors. No effect on usual tensor.

Arguments

TensTYPE(tensor), inout: Tens is returned without modification as it has no symmetries.
idxsINTEGER(*), in: Specify indices to be hashed in regard to the legs of the tensor.
iiINTEGER, OPTIONAL, in: Specify index in terms of array of tensors for generating new hash. If not present, all tensors are set again.

Source Code

show / hide f90 code

Tensors_f90.set_hash_tensorc()[source]¶

fortran-subroutine - October 2016 (dj) Dummy subroutine to comply with interface in qTensors. No effect on usual tensor.

Arguments

TensTYPE(tensorc), inout: Tens is returned without modification as it has no symmetries.
idxsINTEGER(*), in: Specify indices to be hashed in regard to the legs of the tensor.
iiINTEGER, OPTIONAL, in: Specify index in terms of array of tensors for generating new hash. If not present, all tensors are set again.

Source Code

show / hide f90 code

Tensors_f90.split_tensor()[source]¶

fortran-subroutine - October 2016 (dj) Split one index of a tensor into multiple indices.

Arguments

TensTYPE(tensor), inout: Split one index of this tensor.
idxINTEGER, in: Split this index into multiple indices.
SlTYPE(splitlink), in: Information about splitting the tensor.
sidxINTEGER, OPTIONAL, in: Specify which information in Sl is accessed. Default to 1.

Source Code

show / hide f90 code

Tensors_f90.split_all_tensor()[source]¶

fortran-subroutine - October 2017 (dj) Split all links of a tensor.

Arguments

TensTYPE(tensor), inout: Split all links of this tensor.
SlsTYPE(splitlink)(*), in: Contains the information how to split each index. Dimension of Sls must correspond to the rank of the tensor.
sidxINTEGER, OPTIONAL, in: Choose an index within the splitlink information. Default to 1.

Source Code

show / hide f90 code

Tensors_f90.split_tensorc()[source]¶

fortran-subroutine - October 2016 (dj) Split one index of a tensor into multiple indices.

Arguments

TensTYPE(tensorc), inout: Split one index of this tensor.
idxINTEGER, in: Split this index into multiple indices.
SlTYPE(splitlink), in: Information about splitting the tensor.
sidxINTEGER, OPTIONAL, in: Specify which information in Sl is accessed. Default to 1.

Source Code

show / hide f90 code

Tensors_f90.split_all_tensorc()[source]¶

fortran-subroutine - October 2017 (dj) Split all links of a tensor.

Arguments

TensTYPE(tensorc), inout: Split all links of this tensor.
SlsTYPE(splitlink)(*), in: Contains the information how to split each index. Dimension of Sls must correspond to the rank of the tensor.
sidxINTEGER, OPTIONAL, in: Choose an index within the splitlink information. Default to 1.

Source Code

show / hide f90 code

Tensors_f90.trace_tensor()[source]¶

fortran-function - June 2017 (dj) Returns the trace for rank-2 tensors.

Arguments

TensTYPE(tensor), in: Calculate the trace assuming it is a rank-2 tensor.

Source Code

show / hide f90 code

Tensors_f90.trace_tensorc()[source]¶

fortran-function - June 2017 (dj) Returns the trace for rank-2 tensors.

Arguments

TensTYPE(tensorc), in: Calculate the trace assuming it is a rank-2 tensor.

Source Code

show / hide f90 code

Tensors_f90.transposed_tensor()[source]¶

fortran-subroutine - July 2016 (dj) Transposition of indices or permutation.

Arguments

TensTYPE(tensor), inout: Save a transposition/permutation on the indices of this tensor.
permINTEGER(*), OPTIONAL, in: permutation array has length equal to the rank of the tensor with unique entries 1 to rank. Default to rank, rank - 1, …, 2, 1 (transpose)
dopermLOGICAL, OPTIONAL, in: If true, then permute immediately. If false or not present, permutation is only indicated in the indices.

Details

The permutation is only stored in the indices and no actions on the actual memory are carried out. The permutation array [3, 1, 2] is to be read as “The new index 1 comes from old index 3” etc. (template defined in Tensors_include.f90)

Source Code

show / hide f90 code

Tensors_f90.write_tensor()[source]¶

fortran-subroutine - August 2015 (dj) Write the tensor to a file or the std-out.

Arguments

TensTYPE(tensor), in: will be written to given destination.
unitINTEGER, in: write on this unit
formCHARACTER, in: ‘H’ (human readable), ‘B’ (binary) or ‘6’ (non-zero values intended for standard-output).

Details

For form = H or B the information about the rank-3 tensor is written in the following form: 1) three integers, dimension of the tensor 2) H : Entries of the matrix where each entry is in its own line. The tensor is saved row-major (meaning the order of the elements is (1,1,1), (1,1,2), (1,1,3), …, (1,1,d3), (1,2,1), (1,2,2), …). B : elements are written in one step (column-major!).

Source Code

show / hide f90 code

Tensors_f90.transposed_tensorc()[source]¶

fortran-subroutine - July 2016 (dj) Transposition of indices or permutation.

Arguments

TensTYPE(tensorc), inout: Save a transposition/permutation on the indices of this tensor.
permINTEGER(*), OPTIONAL, in: permutation array has length equal to the rank of the tensor with unique entries 1 to rank. Default to rank, rank - 1, …, 2, 1 (transpose)
dopermLOGICAL, OPTIONAL, in: If true, then permute immediately. If false or not present, permutation is only indicated in the indices.

Details

The permutation is only stored in the indices and no actions on the actual memory are carried out. The permutation array [3, 1, 2] is to be read as “The new index 1 comes from old index 3” etc. (template defined in Tensors_include.f90)

Source Code

show / hide f90 code

Tensors_f90.write_tensorc()[source]¶

fortran-subroutine - August 2015 (dj) Write the tensor to a file or the std-out.

Arguments

TensTYPE(tensorc), in: will be written to given destination.
unitINTEGER, in: write on this unit
formCHARACTER, in: ‘H’ (human readable), ‘B’ (binary) or ‘6’ (non-zero values intended for standard-output).

Details

For form = H or B the information about the rank-3 tensor is written in the following form: 1) three integers, dimension of the tensor 2) H : Entries of the matrix where each entry is in its own line. The tensor is saved row-major (meaning the order of the elements is (1,1,1), (1,1,2), (1,1,3), …, (1,1,d3), (1,2,1), (1,2,2), …). B : elements are written in one step (column-major!).

Source Code

show / hide f90 code

Tensors_f90.write_as_matrix_tensor()[source]¶

fortran-subroutine - August 2017 (dj, updated) Write the tensor as a matrix in column-major format. If complex, real part of all entries before complex part of all entries

Arguments

TensTYPE(tensor), in: will be written to given destination.
unitINTEGER, in: write on this unit

Source Code

show / hide f90 code

Tensors_f90.write_as_matrix_tensorc()[source]¶

fortran-subroutine - August 2017 (dj, updated) Write the tensor as a matrix in column-major format. If complex, real part of all entries before complex part of all entries

Arguments

TensTYPE(tensorc), in: will be written to given destination.
unitINTEGER, in: write on this unit

Source Code

show / hide f90 code

Tensors_f90.copy_splitlink()[source]¶

fortran-subroutine - October 2017 (dj) Copy splitlink object.

Arguments

SloutTYPE(splitlink), inout: Copy the entries of Slin here.
SlinTYPE(splitlink), in: source for copy into Slout

Source Code

show / hide f90 code

Tensors_f90.create_splitlink_dimensions()[source]¶

fortran-subroutine - October 2017 (dj) Create a simple splitlink passing the dimensions.

Arguments

SlTYPE(splitlink), inout: Setup this splitlink object.
dimsINTEGER(*), in: Dimension for splitting a tensor link.

Source Code

show / hide f90 code

Tensors_f90.create_splitlink_tensor()[source]¶

fortran-subroutine - October 2017 (dj) Create a splitlink object from the identity matrix.

Arguments

SlTYPE(splitlink), inout: Fill this splitlink object with the splitting for an identity matrix.
IdopTYPE(tensor), in: The dimension is taken from the identity to create the splitlink object.

Source Code

show / hide f90 code

Tensors_f90.create_splitlink_tensorc()[source]¶

fortran-subroutine - October 2017 (dj) Create a splitlink object from the identity matrix.

Arguments

SlTYPE(splitlink), inout: Fill this splitlink object with the splitting for an identity matrix.
IdopTYPE(tensorc), in: The dimension is taken from the identity to create the splitlink object.

Source Code

show / hide f90 code

Tensors_f90.destroy_splitlink()[source]¶

fortran-subroutine - September 2017 (dj) Destroy the object taking care of splitting a link.

Arguments

SlTYPE(splitlink), inout: Deallocate on exit.

Source Code

show / hide f90 code

Tensors_f90.init_splitlink_tensor()[source]¶

fortran-subroutine - September 2017 (dj) Store the information about fusing links in a tensor.

Arguments

SlTYPE(splitlink), inout: Splitlink information is initialized after this subroutine. It needs to be finalized.
TensTYPE(tensor), inout: The tensor to be fused.
idxINTEGER(*), inout: The links to be fused.

Source Code

show / hide f90 code

Tensors_f90.init_splitlink_tensorc()[source]¶

fortran-subroutine - September 2017 (dj) Store the information about fusing links in a tensor.

Arguments

SlTYPE(splitlink), inout: Splitlink information is initialized after this subroutine. It needs to be finalized.
TensTYPE(tensorc), inout: The tensor to be fused.
idxINTEGER(*), inout: The links to be fused.

Source Code

show / hide f90 code

Tensors_f90.finalize_splitlink_tensor()[source]¶

fortran-subroutine - October 2017 (dj) Finalize splitlink is a dummy function for tensors without symmetry.

Arguments

SlTYPE(splitlink), inout: On exit, complete splitlink object. On entry, the hashes are filled with the indices of the corresponding block.
TensTYPE(tensor), in: The tensor which was fused.
idxINTEGER, in: Index of the new link, which has been fused.

Source Code

show / hide f90 code

Tensors_f90.finalize_splitlink_tensorc()[source]¶

fortran-subroutine - October 2017 (dj) Finalize splitlink is a dummy function for tensors without symmetry.

Arguments

SlTYPE(splitlink), inout: On exit, complete splitlink object. On entry, the hashes are filled with the indices of the corresponding block.
TensTYPE(tensorc), in: The tensor which was fused.
idxINTEGER, in: Index of the new link, which has been fused.

Source Code

show / hide f90 code

Tensors_f90.read_splitlink()[source]¶

fortran-subroutine - November 2017 (dj) Write a splitlink object to an open file specified via the unit.

Arguments

SlTYPE(splitlink), in: On exit, splitlink object is filled with data from file.
unitINTEGER, in: Unit where the file is open.
formCHARACTER, in: Specifies type of read between human readable output (‘H’) and binary in an unformatted file (‘B’).

Source Code

show / hide f90 code

Tensors_f90.write_splitlink()[source]¶

fortran-subroutine - November 2017 (dj) Write a splitlink object to an open file specified via the unit.

Arguments

SlTYPE(splitlink), in: Splitlink object to be written.
unitINTEGER, in: Unit where the file is open.
formCHARACTER, in: Specifies type of print between debugging output (‘6’), human readable output (‘H’) and binary in an unformatted file (‘B’).

Source Code

show / hide f90 code

Tensors¶

Previous topic

Next topic

This Page