Python Module exactdiag¶

exactdiag.py Module defines a pure state and a density matrix based on a general abstract quantum system. It defines time evolution methods for those systems.

exactdiag.set_spectrum(val)[source]¶

Set the value for the calculation of the spectrum.

Arguments

valboolean: For calculating the spectrum need True, otherwise False.

exactdiag.runED(params, Operators, Hmpos, sparse=True, maxdim=None)[source]¶

Run all simulation in the list built of parameter dictionaries.

Arguments

paramslist: list of dictionaries where each dictionaries represents a MPS simulation.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
Hmposinstance of MPO.MPO or list of MPO.MPO: Hamiltonian represented in the MPO class.
sparsebool, optional: Flag on the use of sparse matrices. Default to True (use sparse matrices).
maxdimNone or int, optional: Maximal dimension for the complete Hilbert space in order to prevent to large systems for ED. Default to None (no limitation).

exactdiag.runED_threading(params, Operators, Hmpos, threads, sparse=True, maxdim=None, tsleep=30.0)[source]¶

Allows to run ED simulations with threading on a single node.

Arguments

paramslist: list of dictionaries where each dictionaries represents a MPS simulation.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
Hmposinstance of MPO.MPO or list of MPO.MPO: Hamiltonian represented in the MPO class.
sparsebool, optional: Flag on the use of sparse matrices. Default to True (use sparse matrices).
maxdimNone or int, optional: Maximal dimension for the complete Hilbert space in order to prevent to large systems for ED. Default to None (no limitation).
tsleepfloat, optional: Time interval to check for finished jobs.

Details

The multiprocessing module should be taking care to obtain thread-safe processes, but complications might arise from there.

exactdiag.ed_simulation(Hmpo, Operators, param, sparse, maxdim, qtid)[source]¶

Carry out a single static and dynamics simulations for one single set of parameters.

Arguments

Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
paramdictionary: dictionary representing a MPS simulation.
sparsebool: Flag on the use of sparse matrices.
maxdimint: Maximal dimension for the complete Hilbert space in order to prevent to large systems for ED.
qtidinteger: index for multiple realizations of the same simulations, e.g. with quantum trajectories.

exactdiag.dynamic_simulation(Psi, Psi0, Hmpo, Operators, param, sparse, maxdim, qtid)[source]¶

Run the dynamics for a single parameter set.

Arguments

PsiPure state or density matrix.: Quantum state for time evolution. It can either be represented as instance of exactdiag.PureState or as instance of exactdiag.DensityMatrix
Psi0instance of exactdiag.PureState: Quantum state to calculate overlap with the state at every measurement. Meant to be used with the state at time t=0 for the Loschmidt echo.
Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
paramdictionary: dictionary representing a MPS simulation.
sparsebool: Flag on the use of sparse matrices.
maxdimint: Maximal dimension for the complete Hilbert space in order to prevent to large systems for ED.
qtidinteger: If > 0, Psi as an instance of exactdiag.PureState is evolved with quantum trajectories (open system). If 0, instance of exactdiag.PureState is evolved under the Schrodinger equation. If Psi is an instance of exactdiag.DensityMatrix, it is evolved in the Liouville space with the Lindblad master equation and the flag qtid has no effect.

exactdiag.dynamic_circuits(Psi, Psi0, Operators, param, QCin=None)[source]¶

Evolve the quantum system with circuits.

Arguments

PsiPure state or density matrix.: Quantum state for time evolution. It can either be represented as instance of exactdiag.PureState or as instance of exactdiag.DensityMatrix
Psi0instance of exactdiag.PureState: Quantum state to calculate overlap with the state at every measurement. Meant to be used with the state at time t=0 for the Loschmidt echo.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
paramdictionary: dictionary representing a MPS simulation.
callerinstance of QuantumCircuits or None, optional: If QCin is not None, measurements are skipped and the final state is returned. Default to None.

exactdiag.expm_symm_tridiag(diag, sdiag, sc)[source]¶

Calculate exponential of symmetric tridiagonal matrix.

Arguments

diag1d numpy array: diagonal entries (dimension of the matrix)
sdiag1d numpy array: supdiagonal entries
scfloat, complex: scaling inside of the exp(.)

class exactdiag.SymmetrySector(Operators, param, sectorbase=None, empty=False)[source]¶

Taking care of the symmtry. Generates all basis states in the Hilbert space and returns the indices of the states which are conform with the quantum numbers defined for the simulations. The result returned is a list of integers, unless there are no symmetries defined (None).

Arguments

Operatorsinstance of Ops.OperatorList: Contains all operators of the simulation, especially the diagonal generators of the symmetry.
paramdictionary: Contains the simulation setup.
sectorbase2d numpy array, optional: If basis states are calculated manually, a 2d numpy array with a basis state in each row can be passed to initialize the symmetry sector. Number of rows is the number of basis states, number of columns corresponds to the number of sites. For Operators and param are not referenced and None can be passed to them. Default to None.
emptybool, optional: For internal use, no variables are set. Allows for setting them manually. Default to False

Variables

lenint: number of basis states in the symmetry sector.
sectorbase2d numpy array, str: local basis for each basis state of the symmetry sector. If str, filename of the 2d numpy array to be loaded.
sectordicdict: For a tuple with the local basis state the corresponding index is returned. Does not handle key errors.
emptybool, optional: for internal use only. Default to False

__call__(ii)[source]¶

Return the indices of the local basis for the ii-th state.

Arguments

iiint: Consider to ii-th state in the symmetry-sector based basis.

__getitem__(key)[source]¶

Getitem is defined to return the index of a basis state.

Arguments

keylist, array (1d): contains the local basis for each site

__len__()[source]¶: Returns length of SymmetrySector as number of basis states.

get_subspace(idxs)[source]¶

Return the symmetry adapted basis of a subspace.

Arguments

idxslist of integers: these are the sites to be considered for the new space.

permute(perm)[source]¶

Permute sites according to permutation.

Arguments

permlist of ints: Permutation vector.

write(filename)[source]¶

Save the sectorbase of the Symmetry class to hard disk. This is all information necessary to recreate it.

Arguments

filenamestr: Basis string for the file name extended with .npy for the sectorbase matrix.

exactdiag.walls_particles(ll, fill)[source]¶

The distribution of fill particles on ll sites can be described via fill particles and (ll - 1) walls. This iterator yields all possible combinations where 0s represent a wall and 1s represent the a particle.

Arguments

llint: number of sites in the system.
fillint: number of particles distributed on the system.

exactdiag.SingleU1Symmetry(Operators, param)[source]¶

Create symmetry sector for Bose-Hubbard type models with minimum number of particles zero up to some maximum filling.

Arguments

Operatorsinstance of Ops.OperatorList: contains all operators including the generator of the symmetry. It is checked that the symmetry generator is the number operator.
paramdictionary: Contains the simulation setup. It is checked that only one U(1) symmetry is present.

exactdiag.statics_simulation(Hmpo, Operators, param, SymmSec, sparse, maxdim)[source]¶

Complete a static simulation including finding the ground and excited states and measuring those. Returns the ground state if needed for dynamics.

Arguments

Hmpoinstance of MPO.MPO: Hamiltonian written in terms of MPO rules.
Operatorsinstance of the operators class Ops.OperatorList: containing the operators to generate Hamiltonian.
paramdictionary with simulation parameters: settings of the whole simulation.
SymmSeclist or None: list of indices containing the states in the given basis which are in the symmetry sector considered.
sparsebool: flag if sparse matrix should be used for Hamiltonian
maxdimint: limits the dimension of the complete Hilbert space.

exactdiag.statics_state_sparse(Hmpo, param, ii, SymmSec, maxdim)[source]¶

Find a specific state of the Hamiltonian. Returns state and energy (in this order). Function for dense Hamiltonians.

Arguments

Hmpoinstance of MPO.MPO: Hamiltonian written in terms of MPO rules.
paramdictionary with simulation parameters: settings of the whole simulation.
iiint, optional: index of the state to be returned. If 0, ground state is returned, if 1 first excited state and so on. No specific handling for degenerate states. Default to 0 (ground state)
SymmSeclist or None: list of indices containing the states in the given basis which are in the symmetry sector considered.
maxdimint, optional: limits the dimension of the complete Hilbert space.

exactdiag.statics_state_dense(Hmpo, param, ii, SymmSec, maxdim)[source]¶

Find a specific state of the Hamiltonian. Returns state and energy (in this order). Function for dense Hamiltonians.

Arguments

Hmpoinstance of MPO.MPO: Hamiltonian written in terms of MPO rules.
paramdictionary with simulation parameters: settings of the whole simulation.
iiint, optional: index of the state to be returned. If 0, ground state is returned, if 1 first excited state and so on. No specific handling for degenerate states. Default to 0 (ground state)
SymmSeclist or None: list of indices containing the states in the given basis which are in the symmetry sector considered.
maxdimint, optional: limits the dimension of the complete Hilbert space.

class exactdiag._QuantumSystem[source]¶

Abstract type for a quantum system, either pure state or density matrix. Implements general methods equal for both.

apply_op(Op, idx)[source]¶

Apply an operator or gate for any number of sites to the quantum systems. Operatorcan either be for pure states or for density matrices, but is defined in the Hilbert space for both of them

Arguments

Opnp 2d array: containing the operator to be applied, e.g. the propagator of a Hamiltonian or Liouvillian.
idxlist of integers: Apply term to the sites specified here.

apply_op2(Op, ii, ll_1_term=False, perm=False)[source]¶

Apply an operator for two neighboring sites to the quantum system. Operator can either be for pure states or density matrix (Liouville space).

Arguments

Opnp 2d array: containing the operator to be applied, e.g. the propagator of a Hamiltonian or Liouvillian.
iiint: Apply term to the sites ii and (ii + 1).
ll_1_termbool, optional: Boolean to indicate the term ii=L for periodic boundary conditions. Default to False.

delete_rhos()[source]¶: Empty dictionary with reduced density matrices.

dot(*args)[source]¶: General dot product split into different cases, which are detected by the data type.

getset_rho(key)[source]¶

Return the reduced density matrix from the complete wave function.

Arguments

keytuple: containing one or two integers specifying the site indices.

meas_observables(Operators, param, fh, obstype)[source]¶

Measure the observables.

Arguments

Operatorsinstance of Ops.OperatorList: All operators defined for the simulation.
paramdict: containing simulation setup, necessary for MPO measurement.
fhfilehandle: Open file. Results are written to this file handle.
obstypestring: Key to get Observables class in param.

propagate(dt, Hmpo, Operators, param, sparse, maxdim, quenchtime, qt)[source]¶

Time evolution of a quantum system for one time step with either of the following three methods: matrix exponential, Krylov approximation to the matrix exponential, or Trotter decomposition. Method is determined via the convergence parameters.

Arguments

dtfloat: time step (discretization of time).
Hmpoinstance of MPO.MPO: Defines the Hamiltonnian of the system.
Operatorsinstance of Ops.OperatorList: Contains the operators used to build the Hamiltonian.
paramdictionary: Setup for the simulation.
sparsebool: Flag for the use of sparse methods (only referenced for matrix exponential method and (possibly) Krylov).
maxdimint: maximal dimension of the Hilbert space. Only referenced in …
quenchtimetuple of int and float: Storing the number of the quench and the actual time
qtboolean: If True, this as an instance of exactdiag.PureState is evolved with quantum trajectories (open system). If False, instance of exactdiag.PureState is evolved under the Schrodinger equation. If Psi is an instance of a exactdiag.DensityMatrix, it is evolved in the Liouville space with the Lindblad master equation and the flag qt has no effect.

propagate_trotter(dt, Hmpo, Operators, param, quenchtime, qt)[source]¶

Propagate the quantum system with a Trotter decomposition. This function calls depending on the order of the decomposition the exactdiag.PureState.trotter_layer() or exactdiag.DensityMatrix.trotter_layer() for the odd/even part.

Arguments

dtfloat: size of the time step/discretization.
Hmpoinstance of MPO.MPO: Hamiltonian as rule set for the Trotter decomposition.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
paramdictionary: Contains the simulation setup.
quenchtimetuple of int and float: Storing the number of the quench and the actual time
qtbool: If True quantum states are evolved under quantum trajectories, else (False) quantum states are evolved under the Schrodinger equation. For DensityMatrix this should be always False.

Details

The default order for the Trotter decomposition is the 2nd order. The default is overwritten with the order in convergence.TEBDConvParam if this class is given. Possible values are therefore 2 and 4.

reduced(keep, enforce_dense=False)[source]¶

Build the reduced density matrix of the system for a specified set of sites.

Arguments

keeplist of int, optional: Site indices to be kept in reduced density matrix. Must be between 0 < ll - 1 and unique. Consistency with trce is not checked. Default to None (indices are generated from trce)
enforce_densebool, optional: Return reduced density matrix on complete Hilbert space without using symmetries (True). Otherwise symmetries might be used if considered convenient. Default to False.

save(flnm)[source]¶: Save a state as numpy array. Must be implemented by classes themselves.

save_propagator_spectrum(Mat, param, quenchtime, tol=1e-13)[source]¶

Save the eigenvalues of the spectrum of the Hamiltonian or Liouville operator.

Arguments

Mat2d matrix: Contains the Hamiltonian or Liouville operator with the eigenvalues to be determined.
paramdictionary: Contains the simulation setup for one simulation.
quenchtimetuple of integer and float: Contains the number of the corresponding quench and the current time of the simulation.
tolfloat, optional: Tolerance for the check of hermiticity. Default to 1e-13.

Details

traceout(trce, keep=None, enforce_dense=False)[source]¶

Carry out the partial trace on the system returning the density matrix for the remaining system.

Arguments

trcelist of int: Site indices to trace out. Must be between 0 < ll - 1 and unique.
keeplist of int, optional: Site indices to be kept in reduced density matrix. Must be between 0 < ll - 1 and unique. Consistency with trce is not checked. Default to None (indices are generated from trce)
enforce_densebool, optional: Return reduced density matrix on complete Hilbert space without using symmetries (True). Otherwise symmetries might be used if considered convenient. Default to False.

trotter_Ham_2site(Hmpo, Operators, param, quenchtime, even)[source]¶

Build the Hamiltonian for 2 neighboring site containing only local and bond rules.

Arguments

Hmpoinstance of MPO.MPO: Defines the Hamiltonnian of the system.
Operatorsinstance of Ops.OperatorList: Contains the operators used to build the Hamiltonian.
paramdictionary: Setup for the simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time
evenbool: Boolean to switch between even (True) and odd (False) layers in the Trotter decomposition.

class exactdiag.PureState(Psi, ld, ll, SymmSec)[source]¶

Pure state vector for the evolution of closed systems.

Arguments

Psi : 1d numpy array

ldint: local dimension in the Hilbert space
llint: number of sites in the system
SymmSecNone or instance of exactdiag.SymmetrySector: contains the setup of the symmetry if present in the system.

Variables

ddint: dimension of Psi
rhosdict: Storing reduced density matrices for measurements.
lastpropNone, 2d numpy array, or dictionary.: Last propagator used for time independent quenches either as numpy 2d array for the matrix exponential or as dictionary for the Trotter decomposition.
bidxdictionary: Used to store the indices of the subblocks with the same symmetry numbers.

_apply_op2_nosymm(Op, ii, ll_1_term, perm)[source]¶

Apply a two-site operator to the state vector on a specified site.

Arguments

Opnp 2d array: The operator acting on two sites represented as d^2 x d^2 matrix.
iiint: Apply term to the sites ii and (ii + 1).
ll_1_termbool, optional: Boolean to indicate the term ii=L for periodic boundary conditions.

_apply_op2_symm(Op, ii, ll_1_term, *args)[source]¶

Apply a two-site operator to the state vector on a specified site.

Arguments

Opnp 2d array: The operator acting on two sites represented as d^2 x d^2 matrix.
iiint: Apply term to the sites ii and (ii + 1).
ll_1_termbool, optional: Boolean to indicate the term ii=L for periodic boundary conditions.

_apply_op_nosymm(Op, idx)[source]¶

Apply an operator/gate on an arbitrary number of sites.

Arguments

Opnp 2d array: The operator acting on the site represented as matrix.
idxlist of integers: The sites to be contracted with the operator.

_apply_op_symm(Op, idx)[source]¶

Apply an operator/gate on an arbitrary number of sites to a symmetry conserving state.

Arguments

Opnp 2d array: The operator acting on the site represented as matrix.
idxlist of integers: The sites to be contracted with the operator.

_bond_entropy_to_left()[source]¶: Start from ii = ll / 2 and calculate bond entropies going to the left.

_bond_entropy_to_right()[source]¶: Start from ii = ll / 2 + 1 and calculate bond entropies going to the left.

_dot_effhmpo_vec_nosymm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply the effective Hamiltonian represented as MPO / MPO rule set with a vector. For arguments see exactdiag.PureState.dot_effhmpo_vec(). Intended for internal use.

_dot_effhmpo_vec_symm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply the effective Hamiltonian represented as MPO / MPO rule set with a vector. The vector is defined on the symmetry sector specified. For arguments see exactdiag.PureState.dot_effhmpo_vec(). Intended for internal use.

_dot_hmpo_vec_nosymm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply a Hamiltonian represented as MPO / MPO rule set with a vector. For arguments see exactdiag.PureState.dot_hmpo_vec(). Intended for internal use.

_dot_hmpo_vec_symm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply a Hamiltonian represented as MPO / MPO rule set with a vector. The vector is defined on the symmetry sector specified. For arguments see exactdiag.PureState.dot_hmpo_vec(). Intended for internal use.

_get_bond_entropy_nosymm(ii)[source]¶

Calculate the bond entropy for a state of splitting (0, …, ii), (ii + 1, …, L - 1) in a system where no symmetries are used. For description of other arguments look into get_bond_entropies.

Arguments

iiint: Specifies the index of the splitting, where ii is the last site included in the left bipartition.

Notes

Could use scipy.linalg.blas.zherk or scipy.linalg.blas.dsyrk

_get_bond_entropy_symm(ii)[source]¶

Calculate the bond entropy for a state of splitting (0, …, ii), (ii + 1, …, L - 1) in a system with symmetries. For description of arguments look into get_bond_entropies.

Arguments

iiint: Specifies the index of the splitting, where ii is the last site included in the left bipartition.

_get_bond_entropy_symm_sub(ii)[source]¶

_matrix_exp_trotter(Ham)[source]¶

Calculate the matrix exponential considering block diagonal structure if symmetries are present.

Arguments

Hamnp 2d array: matrix representing the Hamiltonian including the time step. To be exponentiated.

Details

Functions accesses self.bidx, a dictionary of tuples or None. Each set of tuples contains the indices for the same symmetry sector and the corresponding site indices.

_quantum_jump_nosymm(Hmpo, param, quenchtime)[source]¶: Apply a quantum jump for the quantum trajectory evolution in a system without any symmetry present. For arguments look into documentation of exactdiag.PureState.quantum_jump(). Intended for internal use.

_quantum_jump_symm(Hmpo, param, quenchtime)[source]¶: Apply a quantum jump for the quantum trajectory evolution in a system with one or multiple symmetries present. For arguments look into documentation of exactdiag.PureState.quantum_jump(). Intended for internal use.

_traceout_nosymm(trce, keep)[source]¶

Trace over a set of sites specified via their indices for states without a symmetry.

Arguments

trcelist of ints: Trace out over the indices contain in this list.
keeplist of ints: Keep the sites whose indices are listed here. Together trce and keep should list all indices exactly one time.

_traceout_symm(trce, keep, SubSec=None)[source]¶

Trace over a set of sites specified via their indices for states with symmetry returning a density matrix considering the symmetry in the larger Hilbert space.

Arguments

trcelist of ints: Trace out over the indices contain in this list.
keeplist of ints: Keep the sites whose indices are listed here. Together trce and keep should list all indices exactly one time.
SubSecinstance of exactdiag.SymmetrySector, optional: If symmetry sector is already calculated, it can be passed with this argument. Otherwise pass None. Default to None.

_traceout_symm2nosymm(trce, keep, *args, **kwargs)[source]¶

Trace over a set of sites specified via their indices for states with symmetry returning a density matrix not considering the symmetry.

Arguments

trcelist of ints: Trace out over the indices contain in this list.
keeplist of ints: Keep the sites whose indices are listed here. Together trce and keep should list all indices exactly one time.
*args, **kwargs: keeping syntax with corresponding method for density matrices.

_trotter_finalize(qt, Hmpo, param, quenchtime)[source]¶

At the end of the Trotter step, the rank-L tensor has to be converted back into the state vector if no symmetry is present. For quantum trajectories it is checked if a jump has to be applied.

Arguments

qtbool: True if evolution with quantum trajectories, otherwise False.
Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class.
paramdictionary: dictionary representing a MPS simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time.

_trotter_initialize(qt)[source]¶

The initialization transfers the vector into a rank-L tensor if no symmetries are present. Furthermore the norm and random number for the quantum trajectories are created before the first time step.

Arguments

qtbool: True if evolution with quantum trajectories, otherwise False.

densitymatrix()[source]¶: Convert the pure state into a density matrix.

distance(State, dist)[source]¶

Measure the distance between the pure state and another quantum state.

Arguments

State1d or 2d numpy array: Represents another pure state (1d) or a density matrix (2d).
distancestr: Define the type of distance measure. Either Trace or Infidelity.

dot(*args)[source]¶: General dot product split into different cases.

dot_effhmpo_vec(Hmpo, Operators, param, quenchtime, maxdim)[source]¶

Multiply the effective Hamiltonian represented as MPO / MPO rule set with a vector.

Arguments

Hmpoinstance of MPO.MPO: defines the effective Hamiltonian through a rule set. The open system part contributes -0.5j Ldagger L (where the imaginary unit is cancelled out when mulitplying with (-1j) in the time evolution.
Operatorsinstance or Ops.OperatorList: containing all operators needed defined on a local Hilbert space.
paramdictionary: setup for the simulation
quenchtimetuple or None: If tuple containing index of quench and present time to obtain coupling.
maxdimint: maximal dimension of the Hilbert space

dot_hmpo_vec(Hmpo, Operators, param, quenchtime, maxdim)[source]¶

Multiply a Hamiltonian represented as MPO / MPO rule set with a vector.

Arguments

Hmpoinstance of MPO.MPO: defines the Hamiltonian through a rule set.
Operatorsinstance or Ops.OperatorList: containing all operators needed defined on a local Hilbert space.
paramdictionary: setup for the simulation
quenchtimetuple or None: If tuple containing index of quench and present time to obtain coupling.
maxdimint: maximal dimension of the Hilbert space

dot_vec(Vec)[source]¶

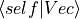Return overlap of wavefunction with other state vector $\langle self | Vec \rangle$ .

Arguments

Vecnp 1d array or instance of exactdiag.PureState: Other vector in the overlap with the PureState.

entropy()[source]¶: Calculate the von-Neumann entropy of the system (always zero for the pure state).

fidelity(Phi)[source]¶

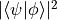Return the fidelity between this state Psi and Phi defined as $|\langle \psi | \phi \rangle |^2$ .

Arguments

Phinp 1d array or instance of exactdiag.PureState: Other vector in the overlap with the PureState.

get_bond_entropies()[source]¶: Calculate the bond entropies for every possible splitting along the chain. Iterator returns ll + 1 numbers.

meas_mpo(Hmpo, Operators, param, quenchtime, maxdim)[source]¶

Measure an MPO defined as rule set, e.g. the Hamiltonian.

Arguments

Hmpoinstance of MPO.MPO: defines the Hamiltonian through a rule set.
Operatorsinstance or Ops.OperatorList: containing all operators needed defined on a local Hilbert space.
paramdictionary: setup for the simulation
quenchtimetuple or None: If tuple containing index of quench and present time to obtain coupling.
maxdimint: maximal dimension of the Hilbert space

norm()[source]¶: Returns the norm of the wave function.

propagate_expm(dt, Hmpo, param, sparse, maxdim, quenchtime, qt)[source]¶

Propagate a quantum state where the propagator is built from a sparse or dense Hamiltonian.

Arguments

dtfloat: size of the time step
Hmpoinstance of MPO.MPO: defines the Hamiltonian through a rule set.
paramdictionary: setup for the simulation
sparsebool: Flag on the use of sparse matrices. If True, sparse matrices will be used.
maxdimint: maximal dimension of the Hilbert space
quenchtimetuple: Tuple containing index of quench and present time to obtain coupling.
qtbool: flag for quantum trajectories.

propagate_expm_qt(dt, Hmpo, param, sparse, maxdim, quenchtime)[source]¶

Propagate a quantum state where the propagator is built from the effective Hamiltonian.

Arguments

dtfloat: size of the time step
Hmpoinstance of MPO.MPO: defines the Hamiltonian through a rule set.
paramdictionary: setup for the simulation
sparsebool: Flag on the use of sparse matrices. If True, sparse matrices will be used.
maxdimint: maximal dimension of the Hilbert space
quenchtimetuple or None: If tuple containing index of quench and present time to obtain coupling.

propagate_gates(func, args=(), return_copy=False)[source]¶

Propagate a quantum state with a set of given gates. At present only 2-site gates are supported.

Arguments

funciterator (__iter__): return gates and left most site index where gate should be applied.
argstuple, optional: arguments for call to the iterator. Default to ()
return_copyboolean, optional: If False, then the state of the class is modified/propagated. The state remains unchanged and a copy of the state after applying the sequence of gates is returned for True. Default to False.

propagate_krylov(dt, Hmpo, Operators, param, sparse, maxdim, quenchtime, qt)[source]¶

Propagate a quantum state taking the exponential in the Krylov subspace.

Arguments

dtfloat: time step
HmpoMPO: Rule set describing the Hamiltonian.
Operatorsinstance of Ops.OperatorList: contains all the operators to setup the Hamiltonian
paramdict: dictionary with simulation setup.
sparsebool: Flag if sparse matrices should be used. Flag only used for small matrices when complete Hamiltonian is built.
maxdimint: maximal dimension of the Hilbert space.
quenchtimetuple or None: contains number of quench and present time.
qtbool: flag for quantum trajectories.

Details

The following modes are available for the Krylov time evolution, which is set in the convergence criteria for the quenches, i.e., convergence.KrylovConvParam with the variable edlibmode:

0 : Built Hamiltonian as matrix and use built-in scipy method.
1 : Built Hamiltonian as matrix and use EDLib Krylov.
2 : Use dot product of MPO and state vector and EDLib Krylov.
3 : As 2, but save Krylov vectors to hard disk to reduce RAM memory usage.
-1 : default. For :math`dim < 2^{10}` take edlibmode=0, then for 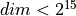$dim < 2^{15}$ use edlibmode=2, otherwise edlibmode=3

Since the Hamiltonian is hermitian, Krylov uses the Lanczos implementation of the algorithm.

propagate_krylov_qt(dt, Hmpo, Operators, param, sparse, maxdim, quenchtime)[source]¶

Propagate a quantum state taking the exponential in the Krylov subspace. Although this is on pure states, we need the Krylov-Arnoldi version to account for non-hermiticity of the expression.

Arguments

dtfloat: time step
HmpoMPO: Rule set describing the Hamiltonian.
Operatorsinstance of Ops.OperatorList: contains all the operators to setup the Hamiltonian
paramdict: dictionary with simulation setup.
sparsebool: Flag if sparse matrices should be used. Flag only used for small matrices when complete Hamiltonian is built.
maxdimint: maximal dimension of the Hilbert space.
quenchtimetuple or None: contains number of quench and present time.

Details

The same modes for the Krylov algorithm are available as described in exactdiag.PureState.propagate_krylov(). Since the effective Hamiltonian is not hermitian, the Arnoldi version of the Krylov algorithm is used.

purity()[source]¶: The purity of a pure quantum state is always 1.

quantum_jump(Hmpo, param, quenchtime)[source]¶

Apply a Lindblad operator for the quantum trajectory evolution. This function works for any time evolution method with an (effective) Hamiltonian (which are matrix exponential, Trotter, Krylov).

Arguments

Hmpoinstance of MPO.MPO: contains the MPO and Lindblad operators.
paramdict: contains the simulation setup.
quenchtimetuple of (int, float): information about the number of the quench and the present time to gain the coupling constants for the Lindblad operators.

save(flnm)[source]¶: Save a state as numpy array. Must be implemented by classes themselves.

trotter_layer(dt, Hmpo, Operators, param, quenchtime, even, qt)[source]¶

Apply an even or odd layer of the Trotter decomposition to the state vector.

Arguments

dtfloat: time step/discretization of the simulation.
Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class.
Operatorsinstance of Ops.OperatorList: Contains the operators used to build the Hamiltonian.
paramdictionary: dictionary representing a MPS simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time.
evenbool: Boolean to switch between even (True) and odd (False) layers in the Trotter decomposition.
qtbool: Flag if using Schrodinger equation (False) or quantum trajectories (True).

trotter_layer_perm(even, ll, pbc)[source]¶

Return permutation to be applied after a complete layer of two-site Trotter terms.

Arguments

evenbool: Indicates if the even or odd layer of the Trotter decomposition was applied.
llint: System size.
pbcbool: Indicates if the Hamiltonian has periodic boundary conditions or not.

trotter_layer_qt(dt, Hmpo, Operators, param, quenchtime, even)[source]¶

Trotter layer under the effective Hamiltonian of the Lindblad master equation representing the hermitian part for an even or odd layer.

Arguments

dtfloat: time step/discretization of the simulation.
Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class.
Operatorsinstance of Ops.OperatorList: Contains the operators used to build the Hamiltonian.
paramdictionary: dictionary representing a MPS simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time.
evenbool: Boolean to switch between even (True) and odd (False) layers in the Trotter decomposition.

class exactdiag.DensityMatrix(Arr, ld, ll, SymmSec)[source]¶

Density matrix for evolution of open systems.

Arguments

Arr1d or 2d np array: If 1d array, a state vector Psi is assumend and the density matrix is built as 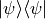$| \psi \rangle \langle \psi |$ . If 2d array, array is assumed to be the density matrix.
ldint: local dimension of the Hilbert space for each site.
llint: number of sites in the system.
SymmSec: None or instance of exactdiag.SymmetrySector: contains the setup for symmetries. If no symmetry is present, pass None.

Variables

Dint: Dimension of the Hilbert space
rho2d numpy array: Density matrix
rhosdict: Storing reduced density matrices
lastpropNone, 2d numpy array, or dictionary.: Last propagator used for time independent quenches. If 2d numpy array, the propagator is stored as matrix. If dictionary, the local propagators for the Trotter decomposition are stored.
bidxdictionary: Used to store the indices of the subblocks with the same symmetry numbers.

_apply_op2_nosymm(Op, ii, ll_1_term, *args)[source]¶

Apply a two-site operator to the density matrix on a specified site. This is the version for density matrices without a symmetry adapted basis.

Arguments

Opnp 2d array: The operator acting on two sites represented as d^4 x d^4 matrix.
iiint: Apply term to the sites ii and (ii + 1).
ll_1_termbool, optional: Boolean to indicate the term ii=L for periodic boundary conditions.

_apply_op2_symm(Op, ii, ll_1_term, *args)[source]¶

Apply a two-site operator to the density matrix on a specified site. This is the version for density matrices with a symmetry adapted basis.

Arguments

Opnp 2d array: The operator acting on two sites represented as d^4 x d^4 matrix.
iiint: Apply term to the sites ii and (ii + 1).
ll_1_termbool, optional: Boolean to indicate the term ii=L for periodic boundary conditions.

_apply_op_nosymm(Op, idx)[source]¶

Apply an operator/gate on an arbitrary number of sites. The gate is defined on Hilbert space, not Liouville space.

Arguments

Opnp 2d array: The operator acting on the site represented as matrix.
idxlist of integers: The sited to be contracted with the operator.

_apply_op_symm(Op, idx)[source]¶

Apply an operator/gate on an arbitrary number of sites to a symmetry conserving density matrix. The gate is defined on Hilbert space, not Liouville space.

Arguments

Opnp 2d array: The operator acting on the site represented as matrix.
idxlist of integers: The sites to be contracted with the operator.

_dot_hmpo_mat_nosymm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply a MPO which can represent the Hamiltonian or a measurement with the density matrix. For arguments look into documention of exactdiag.DensityMatrix.dot_hmpo_mat(). This is the version for density matrices without symmetry adapted basis. Intended for internal use.

_dot_hmpo_mat_symm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply a MPO which can represent the Hamiltonian or a measurement with the density matrix. For arguments look into documention of exactdiag.DensityMatrix.dot_hmpo_mat(). This is the version for density matrices with symmetry adapted basis.

_dot_hmpo_vec_nosymm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply a MPO which represents the Liouville operator with the density matrix represented as superket vector. For arguments look into the documentation of exactdiag.DensityMatrix.dot_hmpo_vec(). This is the version for density matrices without symmetries. Intended for internal use.

_dot_hmpo_vec_symm(Hmpo, Operators, param, quenchtime, maxdim)[source]¶: Multiply a MPO which represents the Liouville operator with the density matrix represented as superket vector. For arguments look into the documentation of exactdiag.DensityMatrix.dot_hmpo_vec(). This is the version for density matrices with symmetry adapted basis. Intended for internal use.

_fidelity_with_state(Phi)[source]¶

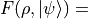
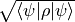Return the fidelity between the density matrix and a quantum state. This is possible independent of the size of the density matrix, since the fidelity simplifies to $F(\rho, | \psi \rangle) =$ $\sqrt{\langle \psi | \rho | \psi \rangle}$ .

Arguments

Phiinstance of exactdiag.PureState or numpy 1D array: Calculate the fidelity to this state vector.

_matrix_exp_trotter(Liou)[source]¶

Taking the matrix exponential of the Liouville operator to obtain the propagator. Without symmetries, the propagator is returned as matrix. With symmetries, a dictionary is returned where the key is the row index and the value are the four local indices plus the matrix element. In the latter case the blockdiagonal structure is used.

Arguments

Lioumatrix: a matrix representing the Liouville operator on two sites in the Liouville space.

Details

Functions accesses class variabes self.bidx, a dictionary of tuples or None. If None, no symmetries are used. If symmetries are used, bidx is a dictionary where each set of tuples contains the indices for the same symmetry sector and the corresponding site indices.

_traceout_first_nosymm()[source]¶: Return the reduced density matrix tracing over the first site in the system. This functions treats density matrices without symmetry.

_traceout_first_symm(SubSec)[source]¶

Return the reduced density matrix tracing over the first site in the system. This function treats density matrices with symmetry and calculates the new density matrix in a symmetry adapted space.

Arguments

SubSecinstance of exactdiag.SymmetrySector: This is the symmetry sector of the system from site 2 to site L (end of the system). It is calculated before hand in order to estimate if a symmetry adapted basis is appropriate.

_traceout_first_symm2nosymm(SubSec)[source]¶

Return the reduced density matrix tracing over the first site in the system. This function treats density matrices with symmetry and calculates the new density matrix in the complete Hilbert space.

Arguments

SubSecinstance of exactdiag.SymmetrySector: This is the symmetry sector of the system from site 2 to site L (end of the system). It is calculated before hand in order to estimate if a symmetry adapted basis is appropriate.

_traceout_last_nosymm()[source]¶: Return the reduced density matrix tracing over the last site in the system. This functions treats density matrices without symmetry.

_traceout_last_symm(SubSec)[source]¶

Return the reduced density matrix tracing over the last site in the system. This function treats density matrices with symmetry and calculates the new density matrix in a symmetry adapted space.

Arguments

SubSecinstance of exactdiag.SymmetrySector: This is the symmetry sector of the system from site 1 to site (L - 1) (L is the end of the system). It is calculated before hand in order to estimate if a symmetry adapted basis is appropriate.

_traceout_last_symm2nosymm(SubSec)[source]¶

Return the reduced density matrix tracing over the last site in the system. This function treats density matrices with symmetry and calculates the new density matrix in the complete Hilbert space.

Arguments

SubSecinstance of exactdiag.SymmetrySector: This is the symmetry sector of the system from site 1 to site (L - 1) (L is the end of the system). It is calculated before hand in order to estimate if a symmetry adapted basis is appropriate.

_traceout_nosymm(trce, keep)[source]¶

Trace over a set of sites specified via their indices for states without a symmetry.

Arguments

trcelist of ints: Trace out over the indices contain in this list.
keeplist of ints: Keep the sites whose indices are listed here. Together trce and keep should list all indices exactly one time.

_traceout_symm(trce, keep, SubSec=None)[source]¶

Trace over a set of sites specified via their indices for states with symmetry returning a density matrix considering the symmetry in the larger Hilbert space.

Arguments

trcelist of ints: Trace out over the indices contain in this list.
keeplist of ints: Keep the sites whose indices are listed here. Together trce and keep should list all indices exactly one time.
SubSecinstance of exactdiag.SymmetrySector: If symmetry sector is already calculated, it can be passed with this argument. Otherwise pass None. Default to None.

_traceout_symm2nosymm(trce, keep, SubSec=None)[source]¶

Trace over a set of sites specified via their indices for states with symmetry returning a density matrix not considering the symmetry.

Arguments

trcelist of ints: Trace out over the indices contain in this list.
keeplist of ints: Keep the sites whose indices are listed here. Together trce and keep should list all indices exactly one time.

Details

This functions is unefficient when tracing over single sites (or small subsystems).

_trotter_finalize(*args)[source]¶: Density matrices without symmetry-adapted basis are converted from the rank-2L tensor back to their matrix representation.

_trotter_initialize(qt)[source]¶

Density matrices without symmetry-adapted basis are converted to a rank-2L tensor.

Arguments

qtboolean: If True, an error is raised because quantum trajectories on a density matrix are not supported. If False, then ok.

distance(State, dist)[source]¶

Measure the distance between the pure state and another quantum state.

Arguments

State1d or 2d numpy array: Represents another pure state (1d) or a density matrix (2d).
distancestr: Define the type of distance measure. Either Trace or Infidelity.

dot_hmpo_mat(Hmpo, Operators, param, quenchtime, maxdim)[source]¶

Multiply a Hamiltonian represented as MPO / MPO rule set with a density matrix.

Arguments

Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class or MPO representing a measurement.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
paramdictionary: dictionary representing a MPS simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time
maxdimint: maximal dimension of the Hilbert space. Only referenced in …

dot_hmpo_vec(Hmpo, Operators, param, quenchtime, maxdim)[source]¶

Multiply a Liouville operator in the Liouville space represented as MPO / MPO rule set with a density matrix represented as superket. The field self.rho has to be converted to the superket before calling the subroutine. Result is returned as superket as well.

Arguments

Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class or MPO representing a measurement.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
paramdictionary: dictionary representing a MPS simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time
maxdimint: maximal dimension of the Hilbert space. Only referenced in …

entropy()[source]¶: Calculate the von-Neumann entropy of the density matrix.

fidelity(Phi)[source]¶

Return the fidelity. Not implemented for any density matrix yet.

Arguments

Phipure state or density matrix: Calculate fidelity to this state. It can be represented as 1d or 2d numpy array, an instance of exactdiag.PureState, or as instance of exactdiag.DensityMatrix.

Details

Implementation for density matrices is missing to avoid calculating the square root of large matrices.

get_bond_entropies()[source]¶

Function to return dummy value for bond entropy. There is no bond entropy defined right now since the eigenvalues do not hold the relation any more.

Details

We could split via SVD for each bipartition.

meas_mpo(Hmpo, Operators, param, quenchtime, maxdim)[source]¶

Measure a MPO using the rule set.

Arguments

Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class or MPO representing a measurement.
Operatorsinstance of Ops.OperatorList (or dictionary): Operators defined used in the simulation.
paramdictionary: dictionary representing a MPS simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time
maxdimint: maximal dimension of the Hilbert space. Only referenced in …

norm()[source]¶: Return the trace as norm of a density matrix.

propagate_expm(dt, Hmpo, param, sparse, maxdim, quenchtime, qt)[source]¶

Propagate a state in the Liouville space according to the Lindblad master equation.

Arguments

dtfloat: time step for evolution.
Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class or MPO representing a measurement.
paramdictionary: dictionary representing a MPS simulation.
sparseboolean: flag if sparse matrix should be used for building Hamiltonian.
maxdimint: maximal dimension of the Hilbert space. Only referenced in …
quenchtimetuple of int and float: Storing the number of the quench and the actual time
qtboolean: If True, evolution should be carried out with quantum trajectories which is impossible for density matrices and therefore an exception is raised. If False, evolution in Liouville space is ok.

propagate_gates(*args, **kwargs)[source]¶: Propagation with gates is not implemented for density matrices

propagate_krylov(dt, Hmpo, Operators, param, sparse, maxdim, quenchtime, qt)[source]¶

Propagation with Krylov using the Arnoldi algorithm.

Arguments

dtfloat: time step for evolution.
Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class or MPO representing a measurement.
Operatorsinstance of Ops.OperatorList: contains the operators defined on the local Hilbert space.
paramdictionary: dictionary representing a MPS simulation.
sparseboolean: Build Liouville operators as sparse or dense matrix. Only accessed in edlibmode=1.
maxdimint: maximal dimension of the Hilbert space. Only referenced in …
quenchtimetuple of int and float: Storing the number of the quench and the actual time
qtboolean: If True, evolution should be carried out with quantum trajectories which is impossible for density matrices and therefore an exception is raised. If False, evolution in Liouville space is ok.

Details

The following modes are available for the Krylov time evolution, which is set in the convergence criteria for the quenches, i.e., convergence.KrylovConvParam with the variable edlibmode:

0 : Built Hamiltonian as matrix and use built-in scipy method.
1 : Built Hamiltonian as matrix and use EDLib Krylov.
2 : Use dot product of MPO and state vector and EDLib Krylov.
3 : As 2, but save Krylov vectors to hard disk to reduce RAM memory usage.
-1 : default. For :math`dim < 2^{10}` take edlibmode=0, then for 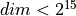$dim < 2^{15}$ use edlibmode=2, otherwise edlibmode=3

Since the Liouville operator is in general not hermitian, Krylov uses the Arnoldi implementation of the algorithm.

purity()[source]¶: The purity of a pure quantum state is always 1.

save(flnm)[source]¶: Save a state as numpy array. Must be implemented by classes themselves.

trace()[source]¶: Return the trace of a density matrix.

traceout_first()[source]¶: Trace-out the first site in the density matrix.

traceout_last()[source]¶: Trace-out the last site of the density matrix.

trotter_layer(dt, Hmpo, Operators, param, quenchtime, even, *args)[source]¶

Apply two site operators for the Trotter decomposition for the odd or even layer.

Arguments

dtfloat: time step for evolution.
Hmpoinstance of MPO.MPO: Hamiltonian represented in the MPO class or MPO representing a measurement.
Operatorsinstance of Ops.OperatorList: contains the operators for building the Hamiltonian and observables.
paramdictionary: dictionary representing a MPS simulation.
quenchtimetuple of int and float: Storing the number of the quench and the actual time
evenboolean: If True, even layer of operators is applied on sites (2k , 2k + 1). If False, we use the odd layer.

exactdiag.idx_symmetry_blocks(Operators, param, ll=2)[source]¶

Generates the indices for blocks conserving the symmetry.

Arguments

Operatorsinstance of Ops.OperatorList: contains all operators, amongst them the diagonal generators of the symmetry.
paramdictionary: containing the string identifiers for the generators of the U(1) and Z2 symmetries.
llint, optional: Number of sites to generate the blocks Default to 2.

Details

If no symmetries are present, the funtion returns None. Otherwise the following output in form of a dictionary is generated. The keys of the dictionary are a tuple of indices in the combined Hilbert space of ll sites with the same quantum number. The value for the corresponding key is a tupled tuple. The i-th tuple contains the local indices for the i-th combined index.

exactdiag.Lidx_symmetry_blocks(Operators, param, ld, ll=2)[source]¶

Function analogous to idx_symmetry_block, but constructing the mapping for the Liouville space used for density matrices:

Arguments

Operatorsinstance of Ops.OperatorList: contains all operators, amongst them the diagonal generators of the symmetry.
paramdictionary: containing the string identifiers for the generators of the U(1) and Z2 symmetries.
ldinteger: local dimension of the Hilbert space.
llint, optional: Number of sites to generate the blocks Default to 2.

Python Module exactdiag¶

Previous topic

Next topic

This Page