Python Module distance

Module defines the two basic distance measures Trace Distance and Quantum Infidelity for density matrices. Moreover the maximum distance over two systems can be determined.

distance.distance(StateA, StateB, dist='Infidelity')[source]

Calculate the distance between two quantum states. States can be either pure states or density matrices. Must be defined on a Hilbert space of equal size.

Arguments

StateA1d or 2d numpy array

Represents the first quantum state as pure state or density matrix.

StateB1d or 2d numpy array

Represents the second quantum state as pure state or density matrix.

diststr, optional

Define the measure used, e.g. Infidelity or Trace distance. Default to Infidelity.

distance.single_site_rho_max_distance(Out1, Out2, ll, dist='Infidelity')[source]

Calculate the maximal distance (infidelity) between the single-site density matrices of two outputs.

Arguments

Out1dictionary

containing the output of the first simulation.

Out2dicitionary

containing the output of the second simulation.

llint

system size

diststr, optional

Choose which distance should be used. Either ‘Infidelity’ (default) of ‘TraceDistance’.

distance.two_site_rho_max_distance(Out1, Out2, ll, dist='Infidelity')[source]

Calculate the maximal distance (infidelity) between the two-site density matrices of two outputs.

Arguments

Out1dictionary

containing the output of the first simulation.

Out2dicitionary

containing the output of the second simulation.

llint

system size

diststr, optional

Choose which distance should be used. Either ‘Infidelity’ (default) of ‘TraceDistance’.

distance.infidelity(StateA, StateB)[source]

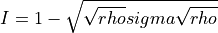
Calculate the infidelity I = 1 - \sqrt{\sqrt{rho} sigma \sqrt{rho}}

Arguments

StateA1d or 2d numpy array

Represents the first quantum state as pure state or density matrix.

StateB1d or 2d numpy array

Represents the second quantum state as pure state or density matrix.

distance.infidelity_psi_psi(psi, phi)[source]

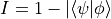Calculate the infidelity of two pure states, which simplifies to I = 1 - | \langle \psi | \phi \rangle.

Arguments

psi1d numpy array

Represents the first quantum state for the distance measurement.

phi1d numpy array

Represents the second quantum state for the distance measurement.

distance.infidelity_psi_rho(psi, rho)[source]

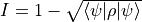Calculate the infidelity of a pure state and a density matrix, which simplifies to I = 1 - \sqrt{\langle \psi | \rho | \psi \rangle}.

Arguments

psi1d numpy array

Represents the first quantum state for the distance measurement, which is a pure state.

rho2d numpy array

Represents the second quantum state for the distance measurement, which is the density matrix.

distance.infidelity_rho_rho(rho, sigma)[source]

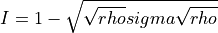
Calculate the infidelity I = 1 - \sqrt{\sqrt{rho} sigma \sqrt{rho}}

Arguments

rho2d numpy array

First density matrix.

sigma2d numpy array

Second density matrix.

distance.tracedist(StateA, StateB)[source]

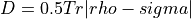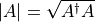Calculate the trace distance D = 0.5 Tr | rho - sigma | with |A| = \sqrt{A^{\dagger} A}.

Arguments

StateA1d or 2d numpy array

Represents the first quantum state as pure state or density matrix.

StateB1d or 2d numpy array

Represents the second quantum state as pure state or density matrix.

distance.tracedist_psi_psi(psi, phi)[source]

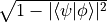
Calculate the trace distance for two pure states, which simplifies to \sqrt{1 - |\langle \psi | \phi \rangle|^2}

Arguments

psi1d numpy array

Represents the first quantum state for the distance measurement.

phi1d numpy array

Represents the second quantum state for the distance measurement.

distance.tracedist_psi_rho(psi, rho)[source]

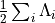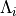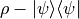Calculate the trace distance for a pure state and a density matrix, that is \frac{1}{2} \sum_{i} \Lambda_{i} where \Lambda_{i} are the singular values of \rho - | \psi \rangle \langle \psi |.

Arguments

psi1d numpy array

Represents the first quantum state for the distance measurement, which is a pure state.

rho2d numpy array

Represents the second quantum state for the distance measurement, which is the density matrix.

distance.tracedist_rho_rho(rho, sigma)[source]

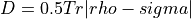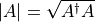Calculate the trace distance D = 0.5 Tr | rho - sigma | with |A| = \sqrt{A^{\dagger} A}.

Arguments

rho2d numpy array

First density matrix.

sigma2d numpy array

Second density matrix.

distance.sqrtm(Math)[source]

Calculate the matrix square root of a hermitian matrix

Arguments

Math2d numpy array (square matrix)

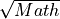Hermitian matrix for calculating \sqrt{Math} of the matrix, not element-wise.

distance.ispure(State)[source]

Inquire if state is a pure state. 1d numpy array are pure states, 2d numpy arrays are density matrices and not pure.

Arguments

State1d or 2d numpy array

Representing the state.