Python Module ops¶
Module Ops.py defines operators, transform operators into their
symmetry-adapted forms in the presence of abelian quantum numbers, and write
operators to Fortran-readable files.
See the manual for more information about the handling of Operators in MPSPyLib.
- class ops.OperatorList(Operators)[source]¶
Defines and handles action on operators for any simulation. Handles transformation to symmetry-adapted operators and writing out the fortran-compatible files. This class still provides the dictionary operators on the operators (
__setitem__,__getitem__,__delitem__,__iter__,__contains__,__len__). If you need more built-in dictionary methods, file a bug report.Arguments
- Operatorsdict
The operators passed in a dictionary to the init method are saved in the corresponding internal dictionary
__oper__.
Variables
- has_complexbool
flag if list contains any complex operators.
- gabelianlist of strings
containing the names of the generators for the abelian symmetry. This can (and is intended) to be updated before writing out operators.
- gdiscretelist of strings
containts the names of the generators for the discrete symmetry. This can (and is intended) to be updated before writing out operators.
__oper__dict (interal use only)dictionary with operators on the complete local Hilbert space.
__qoper__dict (internal use only)dictionary with the symmetry-adapted operators. Deleted when updating generators, generated before writing out operators.
Details
The following keys are blocked for naming operators, since they are all used for the qOperators:
q_d,nqns,npns,q_numbers,q_shifts,q_scales,transformation. Using those keys will return the value of the qOperator dictionary.- OperatorstoQOperators()[source]¶
Return the non-trivial elements of the operators Operators acting on the degeneracy spaces based on the Abelian generators OutGenerators. The generators are assumed to be diagonal. The functions returns a dictionary for the QOperators (see Details for description of the dictionary).
Details
Check for each generator that it is diagonal
Shift values on the diagonal such that the minimum is zero
Scale according to the minimal difference (only considering the neighboring diagonal elements; for zero=1e-10 scaling by one).
Build up unique identifiers: tuple of the (shfted scaled) quantum number of the same i-th element on the diagonal for different generators.
Based on the previous step, we can calculate the degeneracy dimension of each tuple
Generating a hash table: Hash all the tuples and then sort them descending. Use the Square Root of Primers hash defined analogue in fortran. Then create a list of desceding tuples eleminating multiple equal entries.
Connecting bases (transfer matrix
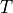 ). The transformation into
the new basis for any operator
). The transformation into
the new basis for any operator 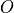 is
is 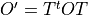 .
.When transforming each operator into the new basis, the operator is block-shaped. Each block is extracted for the corresponding quantum numbers. The size of the block is determined by the degeneracy of the two quantum numbers.
There dictionary has the following keys:
nqns : number of generators (integer)
q_shifts : list of shifts for each generator
q_scales : list of scaling factors for each generator
q_d : dictionary of degeneracy dimension for tuples
q_numbers : the sorted tuples a set (each entry appears only once
transformation : this is the transfer matrix to be applied to the operators.
keys of Operators : dictionary containing a) the key q for the quantum number in a list. Each entry in the list is a list of the two involved quantum numbers. b) the key ‘Blocks’ for the corresponding blocks in a list. Each entry in the list is a matrix.
See the manual for more information about symmetry-adapted operators.
- __contains__(key)[source]¶
Checking if certain key exists in the keys of the dictionary of operators.
Arguments
- keystr (or hashable)
identifier for matrix, intended to be a string with operator name
- __delitem__(key)[source]¶
Delete operator in usual dictionary fashion. Does check if operator is at present generator of symmtry. Does not update the flag
has_complex.Arguments
- keystr (or hashable)
identifier for matrix, intended to be a string with operator name
- __getitem__(key)[source]¶
Return the matrix with the corresponding key in usual dictionary fashion. Returns as well qOperator specific values for blocked keys
q_d,nqns,npns,q_numbers,q_shifts,q_scales,transformation.Arguments
- keystr (or hashable)
identifier for matrix, intended to be a string with operator name
- __len__()[source]¶
Returning the length in the usual dictionary fashion returning the number of elements in the dictionary.
- __setitem__(key, item)[source]¶
Setting matrix in usual dictionary fashion.
Arguments
- keystr (or hashable)
identifier for matrix, intended to be a string with operator name
- item2d np.array
Matrix representing the operator in the local Hilbert space.
- add_abelian(generators)[source]¶
Add the abelian symmetries. If list differs from previous list of abelian generators, the qOperators are deleted.
Arguments
- generatorslist of strings
contains the names of the diagonal generators of the symmetries.
- add_discrete(generators)[source]¶
Add the discrete symmetries. If list differs from previous list of discrete generators, the qOperators are deleted.
Arguments
- generatorslist of strings
contains the names of the diagonal generators of the symmetries.
- check(Op, Add=True, tol=1e-06)[source]¶
Check if an operator op is proportional to one in the operator list Operators. If it is not, Add=True specifies to add it to the list with a random string sequence identifier. Function returns key for operator and the scaling in a list.
Arguments
- Opnumpy 2d array
Check if this operator has an proportional operator in the list of operators.
- Addboolean, optional
Add the operator if (True), otherwise not. Default to True.
- tolfloat, optional
Tolerance for accepting operators as proportional. Default to 1e-6
- check_symmetry(HamMPO, counter, eps=1e-08)[source]¶
Check for every generator that it obeys the symmetry within the MPO given.
Arguments
- HamMPOMPO or list of MPOs
Check with built-in method the symmetry with corresponding generators.
- counterint
if HamMPO is list, check element counter, otherwise not referenced.
- epsfloat, optional
Accept non-zero commutators up to eps, default to
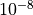 .
.
- get_nqns_npns()[source]¶
The number of abelian and discrete symmetries is defined over the length of the list (assuming no duplicates).
- has_key(key)[source]¶
Built-in method of dictionaries
has_key().Arguments
- key
passed to built-in method
has_key().
- remove_operator(key)[source]¶
Remove an operator from the dictionary of operators.
Arguments
- keystr
string identifier of the operator.
- write(filestub, PostProcess=False)[source]¶
Write out a file defining the operators for use by the Fortran routines It passes back a dict of operators which are keyed by an increasing integer instead of the human-readable keys and the concatenated file name.
Arguments
- fileStubstring
base for the filename concatenated with Ops.dat.
- PostProcesslogical, optional
If PostProcess=True, the operators are not written to file and only the mapping between keys and integers is done. Default to False
Details
The file (Operators) written has the following format:
Number of operators, number of rows and columns in the local Hilbert space.
Matrix elements of each operator in one line
Position of the identity operator.
The file (qOperators) written has the following format:
Number of operators, number of symmetries (nqs)
For each operator, first number of tuples pairs
Indices for mapping of each symmetry [2 * nqs integer]
Indices for the possible degenerate subspace [2 integer]
Value (real or complex entry, either way in one line)
… untill all tuples of this operator
… untill all operators
- write_complex(fileStub, PostProcess=False)[source]¶
Write out a file defining the complex operators for use by the Fortran routines. It passes back a dict of operators which are keyed by an increasing integer instead of the human-readable keys and the complete filename.
Arguments
- fileStubstring
base for the filename concatenated with Ops.dat.
- PostProcesslogical, optional
If PostProcess=True, the operators are not written to file and only the mapping between keys and integers is done. Default to False
- write_q_complex(fileStub, PostProcess=False)[source]¶
Currently not implemented - Write out a file defining the qoperators for use by the Fortran routines. Also passes back a dictionary of operators which are keyed by an increasing integer instead of the human-readable keys.
Arguments
- fileStubstring
base for the filename concatenated with ‘Ops.dat’
- PostProcess: logical, optional
If PostProcess=True, the operators are not written to file and only the mapping between keys and integers is done. Default to False
- write_q_real(fileStub, PostProcess=False)[source]¶
Write out a file defining the qoperators for use by the Fortran routines Also passes back a dict of operators which are keyed by an increasing integer instead of the human-readable keys.
Arguments
- fileStubstring
base for the filename concatenated with ‘Ops.dat’
- PostProcess: logical, optional
If PostProcess=True, the operators are not written to file and only the mapping between keys and integers is done. Default to False
- write_real(fileStub, PostProcess=False)[source]¶
Write out a file defining the operators for use by the Fortran routines It passes back a dict of operators which are keyed by an increasing integer instead of the human-readable keys and the complete filename.
Arguments
- fileStubstring
base for the filename concatenated with Ops.dat.
- PostProcesslogical, optional
If PostProcess=True, the operators are not written to file and only the mapping between keys and integers is done. Default to False
- ops.BuildSpinOperators(spin)[source]¶
Build the spin operators sz, splus, sminus, and identity (I). Spin is the value of the total spin.
Arguments
- spininteger or float
spin value, allowing integer or n * 0.5 with n an integer
Details
Tag operator
Operator
I
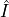
sz
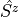
splus
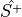
sminus
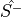
- ops.BuildBoseOperators(Nmax, Nmin=0, spin=0, nFlavors=1, maxFilling=None)[source]¶
Build the bose operators b, bdagger, nbtotal, and identity (I). If spin is nonzero then also build bsz, bsplus, and bsminus. If nFlavors is greater than one then the bose operators contain a flavor index Operators[‘b_flavor’] where flavor=0…nFlavors-1. If spin is nonzero and the bosons are flavorless then the bose operators contain a spin index Operators[‘b_m’] where m=0…2*spin. If both spin and Flavors are nonzero then a set of spinful+flavorful bose operators are built with the indexing Operators[‘b_flavor_m’] where flavor and m are as above.
Arguments
- Nmaxinteger
the maximum total number of bosons allowed on-site.
- Nmininteger, optional
the minimum total number of bosons allowed on-site. default to 0
- spininteger or float, optional
the spin of the bosons. Multiple of 0.5 default to 0
- nFlavorsinteger, optional
the number of “flavors” of boson-basically the number of non-spin internal degrees of freedom. default to 1
- maxFillingoptional
the number of bosons in any one spin or flavor component allowed on-site. This is equal to Nmax for scalar bosons. default to
None
Details
Tag operator
Operator
I
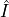
b
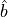
bdagger
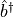
nbtotal
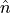
- ops.BuildScalarOperators(Nmax, Nmin, phaseOp=False)[source]¶
Build particle operators with no internal degrees of freedom. Intended for internal use only.
Arguments
- Nmaxinteger
the maximum total number of bosons allowed on-site.
- Nmininteger, optional
the minimum total number of bosons allowed on-site. default to 0
- phaseOpbool, optional
Flag for using phases for fermions originating in the Jordan-Wigner transformation (
True). If not fermions, useFalse. Default toFalse.
- ops.steplexVec(lexvec, n)[source]¶
Step the vector lexvec to the next inferior value in lexicographic order.
Arguments
lexvec : tba
- nint
number of particles
- ops.mult(n, nFlavors, maxFilling)[source]¶
Find the multiplicity of a Hilbert space returned as integer.
Arguments
- nint
number of particles
- nFlavorsint
number of flavors
- maxFillingint
Local Hilbert space has at most maxFilling particles in any one flavor.
- ops.flavorfulHilbertspace(Nmin, Nmax, nFlavors, maxFilling)[source]¶
Build and index a Hilbert space for multiple flavors of particles. The function returns the size of the hilbert space and a set of vectors
stateList[i,:] = [n_{f1}, n_{f2}, ...]giving the occupations of the various flavors in state i. Intended for internal use only.Arguments
- Nminint
Minimum number of particles.
- Nmaxint
Maximum number of particles.
- nFlavorsint
Number of different types of particles.
- maxFillingint
Local Hilbert space has at most maxFilling particles in any one flavor component.
- ops.BosedestructionFromList(stateList, i)[source]¶
Return a bosonic destruction operator from a stateList. Intended for internal use only.
Arguments
stateList : tba
i : tba
- ops.BuildFlavorfulBoseOperators(Nmax, Nmin, nFlavors, maxFilling)[source]¶
Build Bose operators with flavor degrees of freedom. Intended for internal use only.
Arguments
- Nmaxint
Maximum number of particles.
- Nminint
Minimum number of particles.
- nFlavorsint
Number of different types of particles.
- maxFillingint
Local Hilbert space has at most maxFilling particles in any one flavor component.
- ops.BuildSpinfulBoseOperators(Nmax, Nmin, spin, nFlavors, maxFilling)[source]¶
Build Bose operators with spin and flavor degrees of freedom. Intended for internal use only.
Arguments
- Nmaxint
Maximum number of particles.
- Nminint
Minimum number of particles.
- spinfloat (half-integer)
Spin for bosons (there is only one spin for all flavors).
- nFlavorsint
Number of different types of particles.
- maxFillingint
Local Hilbert space has at most maxFilling particles in any one flavor component.
- ops.BuildFermiOperators(Nmax=1, Nmin=0, spin=0, nFlavors=1)[source]¶
Build the Fermi operators f, fdagger, nftotal, FermiPhase, and identity (I). Also build the “phased” operators fP=f.FermiPhase and fdaggerP=fdagger. FermiPhase provided they are linearly independent from f and fdagger. If spin is nonzero then also build fsz, fsplus, and fsminus. If nFlavors is greater than one then the fermi operators contain a flavor index Operators[‘f_flavor’] where flavor=0…nFlavors-1. If spin is nonzero and the fermions are flavorless then the fermi operators contain a spin index Operators[‘f_spin’] where spin=0…2*spin. If both spin and nFlavors are nontrivial then a set of spinful+flavorful fermi operators are built with the indexing Operators[‘b_flavor_spin’] where flavor and spin are as above.
Arguments
- Nmaxinteger, optional
the maximum total number of fermions allowed on-site. default to 1
- Nmininteger, optional
the minimum total number of fermions allowed on-site. default to 0
- spininteger, float, optional
the spin of the fermions. default to 0
- nFlavorsinteger, optional
the number of “flavors” of fermions-basically the number of non-spin internal degrees of freedom. default to 1
Details
Tag operator
Operator
I
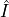
nftotal
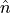
FermiPhase
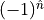
f
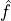
fdagger
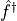
fP
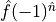 (only if linearly independent of f)
(only if linearly independent of f)fdaggerP
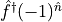 (only if linearly independent of fdagger)
(only if linearly independent of fdagger)
- ops.FermidestructionFromList(stateList, i)[source]¶
Return a fermionic destruction operator from a stateList. Intended for internal use only.
Arguments
stateList : tba
i : tba
- ops.BuildFlavorfulFermiOperators(Nmax, Nmin, nFlavors)[source]¶
Build Fermi operators with flavor degrees of freedom. Intended for internal use only.
Arguments
- Nmaxint
Maximum number of particles.
- Nminint
Minimum number of particles.
- nFlavorsint
Number of different types of particles.
- ops.BuildSpinfulFermiOperators(Nmax, Nmin, spin, nFlavors)[source]¶
Build Fermi operators with spin and flavor degrees of freedom. Intended for internal use only.
Arguments
- Nmaxint
Maximum number of particles.
- Nminint
Minimum number of particles.
- spinfloat (half-integer)
Spin for bosons (there is only one spin for all flavors).
- nFlavorsint
Number of different types of particles.
- ops.BuildFermiBoseOperators(BNmax, FNmax, BNmin=0, FNmin=0, Bspin=0, Fspin=0, BnFlavors=1, FnFlavors=1, maxFilling=None)[source]¶
Build both Bose and Fermi operators in the same Hilbert space. ntotal is the sum of nbtotal and nftotal.
- BNmaxint
Maximum number of bosons.
- FNmaxint
Maximum number of fermions.
- BNminint, optional
Minimum number of bosons. Default to 0
- FNminint, optional
Minimum number of fermions. Default to 0
- Bspinint, optional
Spin of the bosons (eqaul for all flavors). Default to 0
- Fspinint, optional
Spin of the fermions (equal for all flavors). Default to 0
- BnFlavorsint, optional
Number of different types of bosons. Default to 0
- FnFlavorsint, optional
Number of different types of fermions. Default to 0
- maxFillingint or
None, optional Local Hilbert space has at most maxFilling particles in any one boson flavor component. Default to
None.
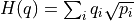 , where
, where 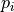 is the
is the
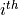 prime.
prime.