Python Module state¶
This module provides various types of initial states. The initial states for the qIMPS routine can be defined via
State.GenerateqInitialState()using the classqProductState.
Non-symmetry conserving MPS states may be obtained through
State.ProductStateState.PartlyProduct
- state.tupleadd(xs, ys, nqns, ncs)[source]¶
Addition of tuples with intermediate conversion to numpy array.
- state.tupledist(xl, xr, mf, nqns)[source]¶
Distance of tuples calculated with conversion to numpy array.
- state.GenerateqInitialState(fileID, qnums, pnums, L, qOperators)[source]¶
Generates an initial state obeying the symmetry according to
State.qProductState.Arguments
- fileIDstr
Basis for the complete file. The complete file name is fileID +
InitialState.dat- qnumslist
List containing the quantum numbers of the U(1) symmetry.
- pnumslist
List containint the quantum numbers for the Z2 symmetry.
- Lint
number of sites in the system
- qOperatorsinstance of
Ops.OperatorList The symmetry conserving operators have to be generated in
Ops.OperatorListbefore creating a qProductState.
- state.GenerateParityState(fileID, L, N0, N1)[source]¶
Generate a product state on L sites with N0 particles in state
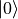 and N1 particles in state
and N1 particles in state 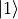 .
N0 + N1 cannot be greater than the system size, but there can
be empty site
.
N0 + N1 cannot be greater than the system size, but there can
be empty site 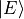 . The particles are placed in
the middle:
. The particles are placed in
the middle: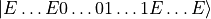
Arguments
- fileIDstr
Basis for the complete file. The complete file name is fileID +
InitialState.dat- Lint
system size.
- N0int
Number of particles in the state 0.
- N1int
Number of particles in the state 1.
- class state.qProductState(qnums, pnums, L, qOperators)[source]¶
Generate an initial state on L sites with the quantum numbers qnums and the Hilbert space in qOperators. The routine attempts to make the state as uniform as possible by defining a mean filling and filling as many sites as possible with that filling. The “exceptional” sites are then filled with the excess quantum numbers. This routine is a work in progress for multiple quantum numbers-MLW 090111.
Arguments
- qnumslist
List containing the quantum numbers of the U(1) symmetry.
- pnumslist
List containint the quantum numbers for the Z2 symmetry.
- Lint
number of sites in the system
- qOperatorsinstance of
Ops.OperatorList The symmetry conserving operators have to be generated in
Ops.OperatorListbefore creating a qProductState.
Details
In the first step generate four lists containing:
meanfilling: rounded quantum number in system divided by system size L. This is done for every quantum number.
excess: Difference between the mean filling just calculated and the targeted quantum number. Negative when mean filling too big. Never used again.
nexceptionall (!!! two l’s at the end !!!): number of exceptional sites.
nrmex: sign/signum function of excess.
Specify particles injected on each iteration. ninject contains the two times the mean filling (except single site) and substracts/adds exceptionall on the last injections
Injections are carried out on two-site blocks. Therefore the quantum numbers on a two-site block is derived and stored in a dictionary.
Select from those two-site blocks, for each injection, the injection which is closest to the mean-filling. E.g. for one quantum number with U(1) symmetry, choose (1, 1) over (2, 0) or (0, 2) for mean-filling of two particles. Z2 symmetries have always a distance of 0.
Write out states is covered through
State.qProductState.write().
- class state.QProductState(qOperators, qnums_per_site=None, pnums_per_site=None, func_subspace=None)[source]¶
Generate an initial state defined by the user. The state is defined in terms of the quantum numbers and must be a product state.
Arguments
- qOperatorsinstance of
Ops.OperatorList The symmetry conserving operators have to be generated in
Ops.OperatorListbefore creating a qProductState.- qnums_per_site2d numpy array (floats), optional
The sites run over the columns, the different quantum numbers run over the rows. At system with 10 sites and 2 abelian quantum numbers has a (2 x 10) shape. Default to None.
- pnums_per_site2d numpy array (floats), optional
The sites run over the columns, the different quantum numbers run over the rows. At system with 10 sites and 2 discrete quantum numbers has a (2 x 10) shape. Default to None.
- func_subspacecallable, optional
Can be used to pass state for degenerate subspace. If not given, an equal superposition is assumed. The function must take the following arguments in exactly this order: (1) dimension of the subspace (2) site index (3) the q-quantum numbers for U1-type symmetries, and (4) the p-quantum numbers for Z2-type symmetries. It must return a vector of the dimension of the subspace.
Details
For degenerate subspaces in one symmetry sector, equal weight is assigned to each state. The functions takes care of the shifting and scaling the quantum numbers to integer-quantum numbers starting at zero.
The system size is deducted from the second dimension of the array qnums_per_site and pnums_per_site. Either qnums_per_site or pnums_per_site must be given.
- qOperatorsinstance of
- class state.ProductState(state_matrix)[source]¶
Create an unnormalized Product (or Fock) state. State will be normalized upon writing. This class can currently not take care of symmetries.
Arguments
- state_matrixnumpy 2d array
The number of sites in the system is defined through the number of columns and the local dimension (equal for each site) through the number of rows. In conclusion each column defines a local state of the global Product/Fock state.
- write(filename, enforce_cmplx=False)[source]¶
Write state to file
Arguments
- filenamestring
Filename for saving the state to file.
- enforce_cmplxBool, optional
Enforce writting a complex MPS even if all entries in the state are real which is necessary when complex Hamiltonians are passed. Default to False.
- class state.PartlyProduct(ld)[source]¶
Define an input state build of pure states possibly defined on several lattice sites. Use the iadd (+=) to add vectors and
mps_state.write()to write your state to a file. This class can currently not take care of symmetries.Arguments
- ldint
local dimension of the Hilbert space
Variables
- ldint
local dimension of the Hilbert space
- purestateslist of numpy 1d array
the list contains state vectors possibly spanning multiple sites. The order in which they are added corresponds the first (left) site to the last (right) site.
- cutofffloat
cut singular values smaller than cutoff. default to 1e-14
- cutchiint
cut bond dimension above cutchi default to 500
Details
Where the Fock state (
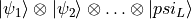 ) this kind of
state can handle entangled sites, e.g. in the case of qubits up to
20 neighboring sites entangled with each other:
) this kind of
state can handle entangled sites, e.g. in the case of qubits up to
20 neighboring sites entangled with each other:
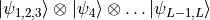
- __iadd__(purestate)[source]¶
Add a state list to the list.
Arguments
- purestatenumpy 1d array
state spanning possible multiple sites. If
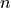 is the
number of sites spanned, the shape with
is the
number of sites spanned, the shape with 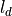 the local
dimension should be
the local
dimension should be 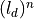 .
.
- check_isometry(tensors)[source]¶
Check isometry and normalization condition
Arguments
- tensorslist of numpy rank-3 arrays
containing the tensors for the initial MPS with orthogonality center on the first site.
- decompose()[source]¶
Decompose pure states spanning multiple sites into tensors. Returned is a list with the local tensors (internal use).
- get_entry_complex(entry)[source]¶
Return the entry of a tensor as a string of a complex number (internal use).
Arguments
- entryfloat, complex float
entry of a tensor
- get_entry_real(entry)[source]¶
Return the (real-valued) entry of a tensor as a string (internal use).
Arguments
- entryfloat
entry of a tensor, real-valued
- has_complex_state()[source]¶
Check for complex states in the list. Return
Trueif complex numbers occur, elseFalse(internal use).
- write(flnm, enforce_complex=False)[source]¶
Write the initial mps state to a file.
Arguments
- flnmstring
filename for the initial mps state.
- enforce_cmplxBool, optional
Enforce writting a complex MPS even if all entries in the state are real which is necessary when complex Hamiltonians are passed. Default to False.
- class state.State(L)[source]¶
This class represents a State object on L sites. (dj: Apparantly it is not used in the library and it is unclear to me how to use it.)
Arguments
- Lint
Number of sites for the state.
Variables
- datadictionary
Dictionary contains keys for system size
Landstatesandweights. The latter two are represented as lists.
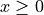 ).
).